空化模型在非定常空化流动计算的应用评价与分析
黄 彪,王国玉,张 博,时素果
(北京理工大学 机械与车辆工程学院,北京 100081)
1 引 言
空化现象不仅和汽液相变过程相关,还涉及到汽液两相的大规模旋涡运动,是一种复杂的非定常多相湍流流动。Arakeri和Acosta采用全息摄影的方法研究了绕轴对称物体的水流中的空化现象,发现空化发生与水流的分离区域的旋涡运动有关。Katz[1]发现分离区域的轴向剪切涡结构影响空化的发展。Laberteraux等[2]利用高速摄像观察发现附着型空化闭合区域存在着空化涡形态结构,王国玉等[3]用高速摄影和录像的方法观察了发生在射流放水阀内部的粘性非定常水流运动,指出空化的形成过程和旋涡运动有关。空化旋涡流动对非定常空化流动的数值模拟提出了巨大的挑战,不仅要求空化模型能精确描述空化的形态发展过程,还要求能够对伴随的大规模旋涡运动进行预测。
近年来,人们为了进行非定常空化流动计算,主要采用了两类空化模型,即正压状态方程的单流体模型和基于相间传输的均相流模型。由于基于正压流体法则,密度和压力项具有相同的变化梯度,斜压矩为零,使得使用正压流体方程不能很好地捕捉实验观测到的空化旋涡流动特性。Kubata[4]、Kunz[5]、Singhal[6]、Senocak和Shyy[8]分别基于相间的传输模型,通过添加不同源项来调节汽液两相间的传输。其中Kubota空化模型和Singhal空化模型在目前得到了比较广泛的应用。蒋增辉等[7]使用商业软件Fluent中的Singhal空化模型,对不同的空泡尾部流场特性进行数值模拟研究。张博等[9]应用商业软件CFX的Kubota空化模型,描述了非定常云状空化形态的发展过程。虽然目前已有较多的使用这些模型来研究非定常空化的文献,但是,由于在一种软件中仅包含一种模型,缺乏对两种模型的应用对比,特别是对空化流场的旋涡流场结构模拟的对比研究还不是很充分。
为了评价空化模型对非定常空化流动中的应用,作者通过商业软件CFX的二次开发技术将Singhal空化模型以及湍流模型镶入了计算软件,分别采用Kubota和Singhal模型计算了绕Clark-y型水翼云状空化流动,分析了不同空化模型对计算结果的影响,特别是对空化流动中的时均速度及涡量场的特性的影响,通过这两种空化模型计算结果和实验现象的对比,对空化模型进行了讨论和评价。
2 数学模型和数值计算方法
2.1 基本方程
假定汽液两相为均相流动,相间无速度滑移,汽液两相的连续方程和动量方程如下所示:

式中,ρ为混合密度,μ为混相介质的动力粘性系数,为速度,P为压强,μt为湍流粘性系数。
2.2 空化模型
2.2.1 Kubota空化模型[4]
Kubota空化模型基于单个空泡的生成和发展时空泡体积变化,基于Rayleigh-Plesset空泡生长方程推导出了如下的蒸发和凝结相的表达式:

式中,RB为平均空泡半径,Fe和Fc分别是蒸发和凝结常数项,随蒸发和凝结而异,设计时应考虑它们发生的速率不同。(凝结通常比蒸发慢得多)
2.2.2 Singhal空化模型[6]
Singhal空化模型在推导过程中基于汽、液两相流模型,由混合密度导出相间质量传输速率,综合考虑了空泡在相变过程中所受阻力和表面张力和实际流体中的非凝结性气体含量的影响。

式中,Ce和Cc是随蒸发与凝结程度不同而变化的经验系数,fv、fg分别为汽相、不溶性气核的质量分数,vch是特征速度,反映气、液两相之间的相对速度。
2.3 RNG k-ε湍流模型及其修正
计算采用了由Yakhot和Orzag提出的RNG k-ε湍流模型:

式中,k、ε 分别为湍动能和湍流耗散率,Gk为湍动能生成项,C1ε和 C2ε为经验常数,σk=σε=1.39,Cμ=0.09。
由于空化区内含有大量的水蒸汽,是一种水汽混合介质,考虑汽液两相混合密度的变化对湍流粘性系数的影响,这里对RNG k-ε模型进行了修正,应用一个密度函数f(ρ)代替(9)式中的混合密度,湍流粘性系数采用以下两式进行计算:

对于(11)式中n的取值,张博等[9]通过取不同的n值,分析了对空化流动数值计算结果的影响,认为在云状空化阶段n取10是合理的。
2.4 数值计算方法
2.4.1 计算网格和边界条件
计算采用了和试验[10]相同的Clark-y型水翼和流动条件。水翼的弦长C=0.07 m。图1给出了计算区域的网格分区及其边界条件。翼型前端的区域采用c型结构化网格划分,这样可以较好地匹配翼型头部的形状。计算区域的入口距翼型前缘为2.5C,出口距翼型尾缘的距离为5C。采用了文献[9]中的网格设置,总网格数为43 000,并如图2所示在翼型周围近壁区域进行了网格加密,近壁面y+值为20~80之间,满足壁面函数要求。
本文采用速度入口、压力出口的边界条件,流动区域上下边界为自由滑移壁面条件,翼型表面采用绝热、自由滑移固壁条件。根据试验工况对计算参数进行相应设置,攻角设定为α=8°,空化数设定为σ=0.8,流速 U∞设定为 10 m/s,对应的雷诺数为 7×105。
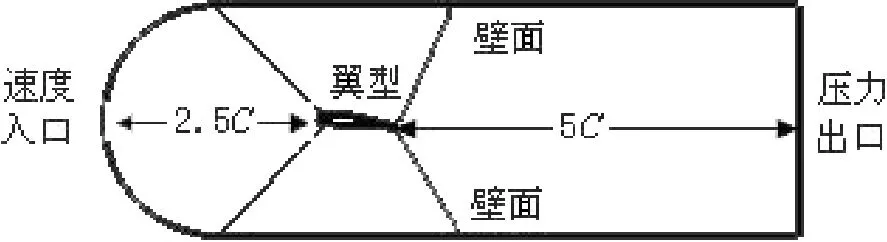
图1 计算区域网格块和边界条件Fig.1 Outline of the computational domain with boundary condition

图2 翼型周围网格Fig.2 Computational grid for flow analysis
2.4.2 无量纲数的定义
计算中的主要无量纲参数为空化数σ和压力系数cp,分别定义为:

这里p∞、U∞和pv分别为距试验段上游入口210 mm处参考断面上的平均静压强、断面平均速度和汽化压强,p为所取试验点的当地压强。
3 结果与讨论
3.1 非定常空穴形态
图3给出了分别采用两种空化模型计算所得空泡形态随时间的变化及其与试验观测结果[8]的对比。图3(a)是试验观测结果,图3(b)、(c)分别为采用Kubota与Singhal空化模型计算得到的结果,计算所得的空泡形态用含汽率分布表示,蓝色区域穴内水蒸气含量基本在80%以上,红色部分基本上为汽相。试验观测所得的空穴形态由图中白色汽相区域表示。

图3 空穴形态随时间的变化Fig.3 Time evolution of cavity shape in the experiment and the calculation
采用Kubota和Singhal空化模型所得的计算结果都清楚地描述了云状空化的产生—发展—脱落的准周期性变化,这与试验观测基本一致。在云状空化开始阶段,如图3,当t=t0+3.5 ms时,翼型头部低压区首先产生厚度很小的微空泡与液滴组成的空穴,此时空穴附着在翼型表面上;随着时间的推移,附着空穴不断地向翼型尾部发展,其厚度沿着翼弦的方向不断增加。在t=t0+14.7 ms时,空穴长度达到最大值,空穴末端达到翼型尾部,这时空穴末端近壁面区域的水汽混合区出现回缩,在t=t0+32.2 ms时,翼型尾部出现大规模的空泡团旋涡脱落现象。
两种空化模型对非定常空化形态的计算结果的主要差异表现在描述空穴回缩、空泡团脱落过程中。采用Singhal空化模型计算结果空泡团是以大尺度旋涡形式脱落,和试验观测的结果基本一致,而采用Kubota空化模型计算的空穴变化主体为空穴整体压缩,随后,在t=t0+32.2 ms时刻空穴断裂成两个部分,空穴前端附着在翼型吸力面上,空穴尾段形成了断裂的空泡团,并向下游运动,和试验观测的流动现象有较大的差异。两种空化模型在模拟空穴形态变化过程中的差异,是由于两种空化模型建立过程对空化现象所做的假设不同造成的。尽管Kubota与Singhal空化模型都是用来描述汽液两相间质量交换的,但Kubota空化模型在推导过程中,将空泡体积变化率作为重要参量,并且假定蒸发与凝结源项与平均空泡半径成反比,空穴的增长和溃灭可以视为无数空泡体积变化的整体行为,空穴内部的含汽量几乎恒定,而Singhal空化模型基于空化流动中敏感的密度变化,空穴内部的密度处于非定常变化的状态,因此采用Kubota描述的云状空化的脱离过程更近视于单个空泡的溃灭过程,而不能体现空化的复杂多相流动特性,而Singhal模型则更多地反映了汽液多相流动过程的大规模漩涡运动,能更精确地描述云状空化的非定常过程。
3.2 绕翼型速度矢量场
为了对比两种空化模型所计算的空化区域的流动结构,分别提取了空泡脱落过程中几个典型时刻绕翼型瞬时速度矢量图,图4为分别采用Kubota、Singhal空化模型计算得到绕翼型瞬时速度场,图5给出了对应时刻翼型尾部局部放大图和试验观测图[10]。

图4 典型时刻绕翼型速度场Fig.4 Instantaneous velocity of cloud cavitation around of the foil

图5 典型时刻绕翼型尾部速度场Fig.5 Instantaneous velocity of cloud cavitation in the rear of the foil
文献[10]中给出了试验中空穴区域内部大规模的旋涡运动过程。指出云状空化后期,在紧贴壁面的区域内诱导了一股指向上游的反向流动,在反向射流的作用下,翼型尾部的大尺度空泡团是以强烈的旋涡分离的形式脱离壁面的。
采用Kubota、Singhal空化模型数值计算的结果均体现了反向射流的产生。t0+17.2 ms、t0+19.6 ms、t0+26.6 ms为空穴开始回缩,反向射流逐渐向翼型前缘发展的时刻。采用不同空化模型所描述的空穴内部的流场结构是相同的:在空泡回缩过程中,采用Kubota空化模型计算得到的结果(图4(a))表明:在翼型尾段近壁面,水汽两相混合区沿壁面反向流动,空穴区域内远离壁面的流体与主流方向一致,在空穴内部,不存在明显的旋涡,而采用Singhal空化模型计算结果(图4(b))会有明显的改善:反向流动向壁面发展,并且在逐渐远离壁面的空化区域内,会产生非常明显的顺时针的旋涡,旋涡有向翼型后上方移动的趋势,使空泡团逐渐脱离壁面,符合实验观测现象。为了进一步阐明流动结构的发展,图5给出了实验与数值计算得到的翼型尾部局部的特写图像,通过对比实验现象可以发现:采用Singhal空化模型准确地模拟出了翼型尾部的空化旋涡区,空泡的旋涡脱落现象非常明显。
3.3 绕翼型旋涡特性
图6为试验[10]和采用不同空化模型获得的云状空化阶段沿来流方向上的速度时均值u沿翼弦的分布,从图中可以看出:在云状空化阶段,主流与空化流中的速度分布存在明显的界面,空穴内部的混合物流动速度由壁面附近呈现出较大的速度梯度变化,并逐渐与主流区的速度相同,点划线a与实线b与翼型表面之间的区域为空化紊流脉动区域,对应于空化旋涡区。对比试验与数值计算的结果,采用Singhal空化模型得到的时均空化紊流脉动区域大小与试验比较接近,Kubota空化模型过高地预计了剪切层的速度梯度变化。

图6 云状空化阶段速度u时均分布图Fig.6 Average streamwise velocity distribution at the cloud cavitation stage
涡量来源于流场存在速度梯度,是描述有旋流动的一个运动学物理量,在研究云状空化现象中,涉及到空泡团脱落等分离流动情况,对涡量进行分析具有很重要的意义,分别采用Kubota与Singhal空化模型对绕翼型涡量场进行描述,利用相关后处理软件得到了对应空化条件下瞬时z向涡量分布图,这里,z向涡量被定义为:

图7为数值计算得到的z向时均涡量沿翼弦的分布。从图中可以看出,由于反向射流的存在,采用不同空化模型计算均可得到:在近壁面处,都会产生旋涡空化区,随着离翼型壁面垂直距离y的不同而变化,同一截面上的涡量均会发生变化,在远离壁面区域,涡量趋近于0。采用不同空化模型计算结果的差异主要体现在对空化旋涡区的模拟上,如图所示,点划线a与实线b与翼型壁面所围成的区域分别为采用Singhal与Kubota空化模型计算得到的空化漩涡区,采用Singhal空化模型计算得到的空化旋涡区域明显比采用Kubota时的大,也就是说,采用Singhal空化模型计算结果体现了更为明显的旋涡特性。

图7 云状空化阶段z向涡量时均分布图Fig.7 Average vorticity distribution at the cloud cavitation stage
不同空化模型在模拟绕翼型云状空化速度与涡量场上的差异反映了不同空化模型所体现的物理机制是不同的,Singhal空化模型在推导相间质量传输速率过程中,添加了瞬时粘性力与湍流波动的影响,综合考虑了汽、液两相间的相对速度、空泡表面张力等诸多因素,从而可更好地考虑空化现象中非常频繁的质量与速度交换,而Kubota空化模型则忽略了空化流动相变过程中频繁的动量交换与湍流波动等因素,所以,在空化区域内,采用Singhal空化模型计算得到的速度以及动量交换要比Kubota空化模型剧烈,体现出更为明显的空化旋涡特性。
4 结 论
分别应用Kubota、Singhal空化模型计算了绕Clark-y型水翼云状空化流动,分析了绕翼型云状空化的空穴形态、空泡团脱落形式、时均速度、涡量场,并与试验结果进行了对比分析,结论如下:
(1)两种空化模型数值计算结果与试验现象均清楚地描述了云状非定常空化过程中的产生—发展—脱落的准周期性变化,但两种模型对空泡团的脱落机理描述是不同的。Kubota模型将脱落过程描述为空泡团的压缩,这和试验结果是不一致的,而Singhal空化模型可以获得和试验观测一致的计算结果。
(2)Kubota空化模型模拟出来的空化旋涡区明显小于试验,而采用Singhal空化模型计算得到的沿翼弦方向的时均速度分布与试验结果一致,可较好地模拟出空化区域内的旋涡空化区域,与实验现象相符。
[1]Katz J.Cavitation phenomena within region of flow separation[J].Journal of Fluid Mechanics,1984,140(4):2397-2436.
[2]Laberteraux K R,Ceccio S L,Mast rocola V J,et al.High speed digital imaging of cavitating vortices[J].Experiments in Fluids,1998,24(6):489-498.
[3]王国玉,曹树良,井小萩利明.剪切层区域旋涡空化的发生机理[J].清华大学学报:自然科学版,2001,41(10):62-64,89.Wang Guoyu,Cao Shuliang,Ikohagi Toshiaki.Vortex cavitation mechanisms in shear layer flow[J].Tsinghua Univ:Sci&Tech,2001,41(10):62-64,89.
[4]Kubota A,Kato H.Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling techniques[J].Journal of Fluids Engineering,1989,111(3):204-210.
[5]Kunz R,Boger D,Stinebring D,Chyczewski T.A preconditioned implicit method for two-phase flows with application to cavitation prediction[J].Comput.Fluids,2000,29(8):849-875.
[6]Singhal A K,Athavale M M.Mathematical basis and validation of the full cavitation model[J].Journal of Fluids Engineering,2002,124:617-624.
[7]蒋增辉,于开平,张嘉钟等.空泡尾部流场特性数值模拟研究[J].船舶力学,2008,12(2):225-230.Jiang Zenghui,Yu Kaiping,Zhang Jiazhong.Numerical simulation on character of the cavity wake region[J].Journal of Ship Mechanics,2008,12(2):225-230.
[8]Senocak I,Shyy W.A pressure-based method for turbulent cavitating flow computations[J].Journal of Computional Physics,2002,176(2):363-383.
[9]张 博,王国玉等.修正的RNG k-ε模型在云状空化流动计算中的应用评价[J].北京理工大学学报,2008,28(12):1065-1069.Zhang B,Wang G,et al.Evaluation of a modified RNG k-ε model for computations of cloud cavitating flow[J].Transac-tions of Beijing Institute of Technology,2008,28(12):1065-1069.
[10]Wang G,Senocak I,Shyy W,et al.Dynamics of attached turbulent cavitating flows[J].Progress in Aerospace Sciences,2001,37:551-581.
[11]王 志,陈九锡.回转体空泡绕流现象的数值模拟[J].船舶力学,2006,8(4):38-43.Wang Zhi,Chen jiuxi.Numerical simulation of cavitation flow on revolution body[J].Journal of Ship Mechanics,2006,8(4):38-43.
[12]Zhou L J,Wang Z W.Numerical simulation of cavitation around a hydrofoil and evaluation of a RNG k-ε model[J].Journal of Fluids Engineering,2008,130(1):1-7.
[13]Coutier-Delgosha O.Numerical prediction of cavitation flow on a two-dimensional symmetrical hydrofoil and comparison to experiments[J].Journal of Fluids Engineering,2007,129(3):279-291.
[14]冯 光,颜 开.超空泡航行体水下弹道的数值计算[J].船舶力学,2005,9(2):1-8.Feng guang,Yan kai.Numerical calculation of underwater trajectory of supercavitating bodies[J].Journal of Ship Mechanics,2005,9(2):1-8.

