主管受撞T型管节点抗冲击性能研究
曲 慧,褚 飞
(1烟台大学 土木工程学院,山东 烟台 264005;2山东建筑大学 土木工程学院,济南 250101)
1 引 言
海洋平台长期在海上工作,环境条件非常恶劣,受碰事故时有发生。Tebbet在《最近五年钢质平台的修理经验》一文中[1],对世界上100起需要修理的海上平台损伤原因,进行了分析,得到将近25%的海上平台损伤是由于碰撞引起的。同时,碰撞事故发生后,可能会导致财产的损失,环境污染和人员伤亡等严重后果。因此,研究海洋平台管桁架的抗冲击性能,将对评价平台结构损伤及碰撞后结构的修复和加固有重要工程意义。
自1983年Soares等[2]对海洋平台管结构进行的冲击性能研究开始,Zeinoddini等[3-5](1998年至2008 年期间)、Bambach 等(2008)[6]、Norman Jones等(2010[7])分别从不同的角度对组成管桁架结构的钢管进行了抗冲击性能研究,这些研究成果为深入分析管桁架结构抗冲击工作机理奠定了基础。同时,金伟良课题组[8-10]、邵炎林等(2006)[11]、王学蕾等(2007)[12]、甘进等(2009)[13]、曲慧等(2010)[14-16]分别采用不同的分析方法,对受船舶或者重物碰撞的海洋平台导管架或平台节点进行了抗冲击性能研究,给出了有关冲击力、变形、能量等方面的计算方法和分析建议。事实上,平台管桁架中的主要传力构件为管节点,节点受撞损坏后的后果将是非常严重的,严重时将导致平台报废,因此深入分析管节点的抗冲击性能将为揭示平台管桁架结构的受撞破坏机制奠定基础。
本文以管桁架结构中最简单的T型管节点为研究对象,采用有限元分析方法,模拟服役中的管桁架节点主管正面受到低速碰撞时的工作机理。
2 有限元模型的建立
2.1 有限元模型的建立
根据《钢结构设计规范(50017-2003)》[17]和实际工程中常用的管节点参数范围,结合管节点分析的力学简图(如图1所示),确定用于机理分析的典型管节点的几何尺寸及特征参数:主管100 mm×4.3 mm×600 mm、支管 70 mm×4.3 mm×300 mm;其各参数值:β=0.49、γ=30、τ=0.67、m=0.46 ton、v=7 m/s。其中,β为支、主管的管径比;γ为主管的径厚比;τ为支、主管的径厚比、m与v分别为冲击锤的质量和速度。采用有限元软件ABAQUS建立三维实体分析模型,如图2所示。分析过程中,主管、支管和冲击锤均采用三维8节点实体单元(C3D8R)。

图1 主管受撞节点力学简图Fig.1 Mechanical sketch for tubular joint impacted on the chord

图2 主管受撞节点有限元模型Fig.2 FEA model of tubular joint impacted on the chord
2.2 材料模型
在冲击荷载下,钢材为率相关材料。本文是通过Cowper-Symonds[18]模型来模拟的,该模型能够利用依赖于应变率的参数来确定屈服应力,其动态屈服函数为:

上式中,D、n为Cowper-Symonds模型的应变率参数,其中,σdy为钢材的动态屈服强度,σy为钢材的静态屈服强度,ε˙为钢材所经历的应变率,参考Zeinoddini[3]的文献,取D=100 s-1,n=10。如表1给出了钢材材料特性的相关参数取值。

表1 钢材材料参数Tab.1 Material characteristics of steel
锤体在撞击过程中变形很少,基本上处于弹性阶段,因此在有限元模型中均采用线弹性模型。在有限元模型中,为节约计算的机时,用一个与支管直径相同、高度为100 mm的圆柱体替代,对于不同质量的锤体,质量取为与实际质量相等,而密度通过换算得到。
2.3 边界条件、荷载及界面处理
按照管桁架计算简图(图1),将节点分析的边界条件设定如下:主管两端和支管的端部均为铰支,即主管、支管端部中线U1,U2,U3三个自由度均被约束;通过有一定质量和速度的锤体,将冲击力沿支管轴线施加在节点上。速度通过*FIELD_INITIAL_VELOCITY_TRANSLATION ONLY施加。
分析过程中,冲击锤与端板顶面之间的接触采用*CONTACT_SURFACE_TO_SURFACE(普通面面接触),在FRICTION FORMULATION采用PENALTY,并设定摩擦参数为0.3。端板底面与支管端口之间,考虑到实际中两者间是采用焊缝连接的,接触采用*CONSTRAINT_TIE_SURFACE_TO_SURFACE进行设定。
3 管节点的变形发展及分析
为能够清晰表达变形过程中节点的变形情况,将各特征点在图3中标识出来。

图3 主管受撞过程中接触点位置示意图Fig.3 Contact point scheme on the chord during impact
3.1 变形发展过程
图4为节点在不同时刻的变形情况。锤头首先与主管表面最外边线EF接触;随后锤头下行,当t=2.5 ms时(图(b)),锤头与试件的接触面积不是很大,图中红色Mises应力分布只是接触面周围区域,在E、F两点有应力集中现象。随着时间的增加,主管管壁的发生局部凹陷变形,锤头与主管的接触面积逐渐增加,由图(c)、(d)即在 t=5 ms、t=7.5 ms时,可以明显地看到,红色的Mises应力分布逐渐向主管的两端传开。由图(e)和(f)可以明显地看出主管局部凹陷变形已经很大。由图(g)可以看出主管管壁上有明显的与锤头形状相同的凹陷区域,此凹陷区域的周围的应力达到σ=486.9 MPa,该值大于主管钢材的屈服应力σy=447 MPa,说明在此凹陷区域形状的外包线处形成塑形铰线。在t=16 ms时锤头与开始反向运动,图(h)、(i)、(j)、(k)和(m)清晰地展示了随着锤头逐渐离开节点,主管管壁逐渐发生弹性恢复。在t=24.5 ms时与节点完全分离,故由图(m)可以形象地看出“8”字形塑形铰线。
3.2 主管受撞破坏模态分析
冲击过程中,当锤头冲击管节点时,节点跨中向下弯曲,支座发生转动。主管管壁发生局部向内凹陷,在锤头逐渐离开试件的过程中,主管管壁局部凹陷变形有较大的弹性恢复。
图5给出了T型管节点在圆柱体锤头作用下的变形。从图中可以看出,钢管的变形主要由两部分构成,一部分为主管受到锤头冲击后的局部凹陷,另一部分为管节点的整体弯曲变形。节点的变形可视为两种变形的耦合。由图(d)可以明显地看出,冲击过程中,节点整体弯曲变形很小,主管管壁的局部凹陷屈曲变形占主导地位。
从图(b)看出,主管管壁的局部凹陷呈一个碗型,主管和支管的交界处并没有发生明显的局部变形。在冲击荷载作用下,先发生局部屈曲变形的部位是与锤头接触的主管管壁,这主要是因为主管是一个薄壁型圆管,主管的管壁刚度较小,在接触到锤头时首先在接触面上发生局部屈曲;当冲击能量不是很大时,仅靠主管管壁的局部凹陷变形即可把全部能量吸收掉,故主、支管交界处不会发生凹陷变形来吸收能量。只有当冲击能量很大时,主、支管交界处才会发生凹陷变形吸收冲击能量。
在锤重m=460 kg,冲击速度v=7 m/s的冲击荷载作用下,节点支管未发生明显的变形,主管下部与锤头接触位置发生了局部凹陷,整体弯曲变形不明显(见图(d));从图中还可以看到主管下部在圆柱体锤头作用下的接触面上有清晰的“8”字形凹陷区域(见图(a))。主管管壁沿着凹陷区域边缘发生受弯屈服,形成“8”字形塑性铰线(见图6)。

图5 主管受撞变形图Fig.5 Deformation and stress of chord after impact
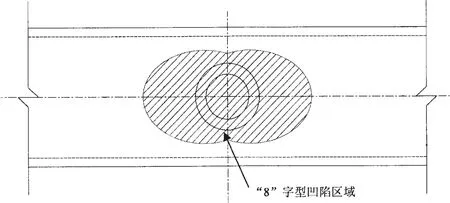
图6 节点凹陷区域形状示意图Fig.6 Scheme of concave zone shape for joint
4 管节点的工作机理分析
4.1 主管受撞冲击力时程曲线
冲击力时程曲线反映了从锤头和试件接触到锤头第一次反弹之间时间段的冲击力随时间变化的情况。结合节点的变形发展过程,从图7冲击力时程曲线可以分析得出,锤头对试件的冲击过程主要可以分为四个阶段。阶段一、锤头与试件接触,冲击力随时间呈直线变化关系;在锤头与构件刚开始接触时,冲击力与时间呈直线增长关系,说明在此过程中主管管壁主要发生弹性变形。在t=2.5 ms时冲击力随时间增长的斜率开始下降,说明在此刻构件的刚度开始变小,这主要是因为主管管壁在锤头作用下发生了局部凹陷变形,刚度降低。在t=3 ms时,冲击力发生下降段,其原因为在此阶段主管管壁发生跃越屈曲,管壁向内凹陷的速度大于锤头落下的速度,因此锤头与管壁有相互分离的趋势。在下降段持续大约t=1 ms后,冲击力又随时间的增长而呈现直线增长。这主要是因为主管管壁在发生一定的局部凹陷后就不再继续变形,管壁达到稳定状态,冲击力不再继续下降,而锤头继续下落接触到试件,因而冲击力会继续随时间而增长,而且呈直线增长,在t=4.4 ms时达到最大值,其后又由于主管管壁发生局部凹陷冲击力有少许下降。阶段二、冲击力达到峰值后迅速下降,并且发生剧烈的波动,这一过程大约持续t=6~8 ms,在局部失稳的开始阶段,管壁迅速向内凹陷,凹陷的速度超过了锤体的下落的速度,导致支管与锤体有相互分离的趋势,这在冲击力时程曲线中反映为冲击力迅速下降,并在管壁达到稳定状态时停止下降,由于在这一阶段主管壁不断向内凹陷,不断地从一个稳定状态到另外一个稳定状态,这在曲线中反映为冲击力随着时间不断的波动。阶段三、在t=11.4~16 ms之间,冲击力曲线趋于平稳,且随时间的增长冲击力保持不变。这主要是因为在这一阶段中主管管壁的局部凹陷值达到一定值后趋于稳定,由于支管在平面内的支撑作用,即使有整体弯曲变形的发生但是也是很小,所以这一阶段主要是管壁发生的局部凹陷达到极限时,在其周围逐渐形成塑形铰(见图5(a))。阶段四、冲击力时程曲线急剧下降,这一阶段主要是因为在t=15.7 ms时,锤头反向运动,与构件呈相互分离趋势,所以冲击力随时间增大而急剧下降。到t=24.6 ms时锤头与节点完全分离,此时冲击力降为0。

图7 冲击力时程曲线Fig.7 Impact force time history curve

图8 变形点B、C的位置示意图Fig.8 Position scheme of deformation points B and C
4.2 主管受撞变形时程曲线
本文所测变形点B、C分别为锤头中心所对应的主管上表面和主管中轴横向最外侧点(见图8),图9(a)、(b)分别为点B在冲击荷载作用下沿支管轴向(即图中所示Y轴方向)和点C沿垂直于主管轴线与支管轴线平面方向(即图中所示X轴方向)的变形随时间变化的情况。两图主要揭示了主管管壁局部变形随时间变化的情况,因为支管对节点的平面内的支撑作用,限制了节点在平面内的弯曲变形,整体变形不明显,所以没有对其进行深入分析。

图9 变形时程曲线Fig.9 Deformation time history curve
由图9的变形时程曲线可以得出,B、C两点的变形曲线形状基本相同,两者的变形趋势基本相同,B点下陷变形远大于C点侧向鼓曲变形。参照冲击力时程曲线的划分方法,将变形曲线也分为四个阶段。阶段一、曲线随时间呈直线增长关系,说明此阶段主管管壁的变形为弹性变形。阶段二、曲线的变化率逐渐减小,说明在此阶段主管管壁的塑形变形逐渐增加。阶段三、曲线的变化率随时间的增长变得越来越小,到t=15.7 ms时,B、C点变形达到最大值,B点最大变形值为δ=61.42 mm,C点最大变形值为δ=15.17 mm。阶段四、在t=15.7 ms之后锤头开始向上运动,所以主管管壁变形在达到最大值后,随着锤头与节点的相互分离,主管管壁逐渐发生弹性回弹,B、C点变形随时间减小。锤头与节点完全分离后,即在t=26 ms之后,B、C点的变形不再变化,在δ-t曲线上表现为平直线段。主管管壁上B点不可恢复的塑形变形δ=46.55 mm,C点不可恢复的塑形变形δ=10.9 mm。
4.3 主管受撞速度时程曲线
图10为锤头的速度时程曲线。从图中可以得出,节点受撞时,锤头的初速度v1=7 m/s,在阶段一、二、三过程中,锤头速度随着节点逐渐发生变形吸收锤头传来的动能而减小;在阶段三结束时,即t=15.7 ms时,锤头的速度减小为零。阶段四,由于初始动能Ι=/2没有被节点完全吸收掉,所以在锤头速度降为零之后又开始反向运动,以动能的形式再把剩余的能量消耗掉,因此完全符合能量守恒定理。随着锤头与节点完全分离,即在t=22.6 ms后锤头的速度保持不变v2=2.24 m/s(见图10段A)。

图11 C点E22方向应变时程曲线Fig.11 Strain time history curve of E22 direction for point C

图10 锤头速度时程曲线Fig.10 Velocity time history curve of hammer
4.4 主管受撞应变时程曲线
图11为主管表面C点沿Y轴(见图8)方向应变,简称C点E22方向应变。分析主管上表面C点应变时程曲线可以得出:当主管受撞时,C点E22方向应变表现为拉应变;阶段一、C点的E22方向应变在初始阶段随时间呈直线增长,在t=2 ms时,曲线突然下降即应变突然减小,说明此刻节点发生局部跃越屈曲。阶段二、阶段三,应变随时间增长的逐渐增加,但变化率逐渐减小,在阶段三末C点的E22方向应变达到峰值。阶段四、随着锤头的反向运动,主管管壁的弹性变形开始逐渐恢复,所以C点的E22方向应变随时间逐渐减小。当锤头与试件完全分离后,应变保持不变。对应变时程曲线进行微分,得到最大应变率为9.1×10-3/s。把最大应变率代入(1式)来确定屈服应力,计算出的动态屈服应力的为623.3 MPa,其相对静态屈服应力增大系数e=σdy/σy=623.3/447=1.4,说明在动力作用下,钢材的屈服强度增大了1.4倍。
4.5 主管受撞冲击力变形关系曲线
由图12可以看出,初始加载时,在δ=0~2 mm之间时,冲击力随变形的增加几乎成线性的关系;在位移达到δ=2 mm后,冲击力变形曲线的变化率开始变小,说明节点刚度逐渐发生退化,刚度退化的原因为构件主管管壁发生了局部凹陷变形;但在δ=2~3.5 mm之间,冲击力依然随变形的增加而增大,但刚度明显降低。在δ=3.5~6.9 mm的变形区间内,冲击力随变形增大而增加不多,且有随变形的增大而上下波动的现象,说明在此阶段节点主管管壁局部区域主要在逐渐发生塑性变形。变形达到δ=6.9 mm后,随后变形的增大冲击力有一个线性下降段,说明在此阶段节点的主管管壁局部区域发跃越屈曲,B点其向内变形的速度大于锤头下落的速度,锤头与节点有相互分离的趋势。当达到δ=10 mm时冲击力不再下降,在δ=10~13 mm之间冲击力开始随着变形而呈直线增加。说明此阶段节点局部屈曲趋于稳定,锤头与主管上表面重新完全接触。在δ=13~21.5 mm这一阶段,冲击力随变形的增加呈现直线增加关系,在变形达到δ=21.5 mm时,冲击力达到最大值。随后冲击力随变形的增加呈现出比较剧烈的上下波动,而冲击力大小却没有太大变化,主要是因为主管管壁在这一阶段不断向内凹陷,不断地从一个稳定状态到另外一个稳定状态,直至变形达到最大值。出现这种现象的原因是:节点在主管上表面发生塑形变形,并在其管壁上逐渐形成塑形铰线,当完全形成塑形绞线时,变形达到了最大值。之后,节点进入卸载阶段,节点的弹性变形有所恢复,卸载段的刚度小于加载初期的弹性刚度,这说明试件在受到冲击后发生较大的损伤,导致刚度下降。

图12 冲击力变形曲线Fig.12 Impact force versus deformation relationship curve

5 结 论
本文通过对主管受到碰撞的管桁架T型节点的变形发展过程分析,确定节点的破坏模态;在对冲击力、位移、应变和落锤速度等时程曲线的分析中,揭示抗冲击性能机理,并得到如下结论:
(1)主管受撞的T型管节点变形以受撞区域的主管上表面发生局部屈曲为主,节点的整体变形相对较小。在冲击过程中,在主管上表面形成“8”字型塑性铰线。
(2)在冲击过程中,主管上表面凹陷和侧面鼓曲的趋势是一致的,只是凹陷程度要远大于侧向鼓曲程度。
(3)冲击可以使组成节点的钢材屈服点明显提高。
(4)冲击过程主要分为弹性、塑性屈服和卸载三个阶段,卸载刚度要低于节点初始刚度,冲击过程中能量保持守恒。
[1]Tebbett I E.The last five year,5 experience in steel platform repairs[C]//Proeeeding of 19th Annual Offshore Technology Conference.OTC5385,1987:261-268.
[2]Spares C G,Soreide T H.Plastic analysis of laterally loaded circular tubes[J].Journal of Structural Engineering,1983,109(2):451-467.
[3]Zeinoddini M,Harding J E,Parke G A R.Effect of impact damage on the capacity of tubular steel members of offshore structures[J].Marine Structures,1998,11(4-5):141-157.
[4]Zeinoddini M,Parke G A R,Harding J E.Axially pre-loaded steel tubes subjected to lateral impacts:An experimental study[J].International Journal of Impact Engineering,2002,27(6):669-690.
[5]Zeinoddini M,Harding J E,Parke G A R.Axially pre-loaded steel tubes subjected to lateral impacts(a numerical simulation)[J].International Journal of Impact Engineering,2008,35(11):1267-1279.
[6]Bambach M R,Jama H,Zhao X L,Grzebieta R H.Hollow and concrete filled steel hollow sections under transverse impact loads[J].Engineering Structures,2008,30(10):2859-2870.
[7]Jones N,Birch R S.Low-velocity impact of pressurized pipelines[J].International Journal of Impact Engineering,2010,37(2010):207-219.
[8]金伟良,龚顺风,宋 剑,谢 彬,孙章权,刘 健.大型船舶碰撞引起的海洋导管架平台结构损伤分析[J].海洋工程,2003,21(2):20-25.
[9]金伟良,宋 剑,龚顺风.船舶与海洋平台撞击的荷载模拟[J].计算力学学报,2004,21(1):26-32.
[10]Jin W L,Song J,Gong S F,Lu Y.Evaluation of damage to offshore platform structures due to collision of large barge[J].Engineering Structures,2005,27(2005):1317-1326.
[11]邵炎林,何炎平.海洋结构物中典型圆管构件的碰撞损伤研究[J].中国海洋平台,2006,21(1):35-40.
[12]王学蕾,张延昌,王自力.海洋导管架平台K型节点碰撞性能研究[J].江苏科技大学学报(自然科学版),2007,21(4):1-6.
[13]甘 进,潘 晋,吴卫国,朱孟巍.船舶与导管架平台碰撞的动力响应研究[J].船海工程,2009,38(5):153-156.
[14]曲 慧,张 云,邵永波.T型管节点抗冲击性能工作机理分析[J].船海工程,2010,39(4):161-164.
[15]Qu H,Zhang Y.Mechanism analysis of impact performance for tubular T-joint[C]//12th International Conference on Inspection,Appraisal Repairs&Maintenance of Structures.Yantai,China,CI-Premier,2010:159-162.
[16]Song S Z,Qu H,Shao Y B.Impact strength for tubular T-joint with reinforced chord under axial impact force[C]//12th International Conference on Inspection,Appraisal Repairs&Maintenance of Structures.Yantai,China,CI-Premier,2010:167-172.
[17]中华人民共和国国家标准GB50017-2003.钢结构设计规范[S].北京:中国计划出版社,2003.
[18]Symonds P S.Survey of methods of analysis for plastic deformation of structures under dynamic loading[R].Brown University,Division of engineering report,BU/NSRDC/1 67,1967.

