救生舱的结构的优化设计与试验分析

许佩霞，胡 勇

（1江南大学 机械学院，江苏 无锡214122；2中国船舶科学研究中心，江苏 无锡214082）

1 引 言

在世界援潜救生史上，救生钟是唯一完成与失事潜艇对接并成功救援的援潜救生装备，也是历史最为悠久的潜艇他救装备。救生舱是救生钟（或救生艇）的关键耐压结构，其重量可占系统总重量的50%以上。根据设计深度的不同，该结构提供的浮力可占总系统的60%-80%。由此可见，救生舱的设计对救生钟（艇）的战技性能有极大影响。当救援舱的浮力重量比难以有效增加时，只有通过减少救援舱的内部尺寸并增加浮力材料来控制全系统的重浮力平衡。如我国最新的LR7深潜救生艇的救援舱直径仅为1.5m。这是以牺牲人员舒适性为代价来降低系统重量。由此可见，对救生舱的结构优化是救生钟（艇）耐压结构设计的主要工作之一。对于救生舱的优化设计，在满足工作深度要求条件下，以较轻的耐压壳体重量获取较大的密闭耐压空间，即浮重力比最大化是评价耐压结构的设计是否优化的重要指标。本文针对救生舱的耐压结构进行了优化分析，在满足规范要求的基础上，开发了一套优化设计程序，用于寻找最优结构尺寸。在此基础之上，本文设计了一只救生舱结构。对设计的救生舱进行了耐压试验考核验证，获得了典型部位的应力应变分布。通过试验证明该优化设计合理，救生舱满足设计要求。

2 救生舱的优化设计方法

对于救生钟（艇）而言，救生舱的耐压结构均为环肋圆柱结构、球形或扁球形封头结构、救生舱门开口加强结构等典型结构构成。各船级社设计规范对这些结构的强度和稳定性的校核有明确规定[1-2]。各规定值全部满足规范要求且同时接近规范可认为是最优承载结构尺寸。该结构尺寸下的救生舱浮重比最大。但是，最优承载结构尺寸并非最佳设计尺寸。在最优承载结构尺寸的基础上，进一步考虑全系统总布置要求、施工工艺要求、原材料进货要求等因素，对结构进行二次优化，得到最终的优化设计方案。

2.1 环肋圆柱壳体的优化设计

受外压的环肋圆柱壳的主要破坏形式有以下三种：

（1）强度破坏；

（2）筋间壳板失稳破坏；

（3）总体失稳破坏。

三种破坏形式的极限破坏压力通常是不一样的。当三种破坏形式的极限压力比较接近时，可以认为结构的效率最高。

参考潜艇及潜水器规范要求，超大潜深救生钟的环肋圆柱壳结构应满足以下约束条件：壳板跨中中面周向应力

壳板跨端内表面纵向应力

肋骨应力

筋间壳板屈曲压力

总体屈曲压力

环肋圆柱壳的优化设计以满足主尺度条件下壳体最轻为目标函数。以潜艇结构设计计算方法中规定的最小应力要求和最小稳定性要求为约束条件，即在满足（1）～（5）式的条件下重量最轻。

环肋圆柱壳的半径R，总长L为已知量。壳板的厚度t，肋骨间距l，加强筋的剖面面积F和加强筋的惯性矩I为四个未知变量。在这四个未知变量中，加强筋的剖面面积F和惯性矩I不是相互独立的变量。如果采用球扁钢作为加强筋，其剖面面积和惯性矩依型号而定。因此，在不同球扁钢型号下，可把F和I视为定值，这样只有t和l两个独立变量确定结构的几何尺寸。在满足（1）～（5）式的条件下，耐压壳体相对比重最小的几何尺寸定为最优方案。

因此，分别取不同型号球扁钢为加强筋，以t和l为独立变量，同时满足以下不等式组：

上面不等式组中，K、K1、K2和Cs均是与参数u、β相关，可查图谱而定。为了便于程序计算，将图谱回归成二元二次多项式，具体回归办法如下：

（1）利用系数的数值表结果，首先利用最小二乘法原理回归出fu=u0（β）；

（2）计算出β相对于u0的影响系数。

利用两元非线性回归分析可得到如下的计算公式：

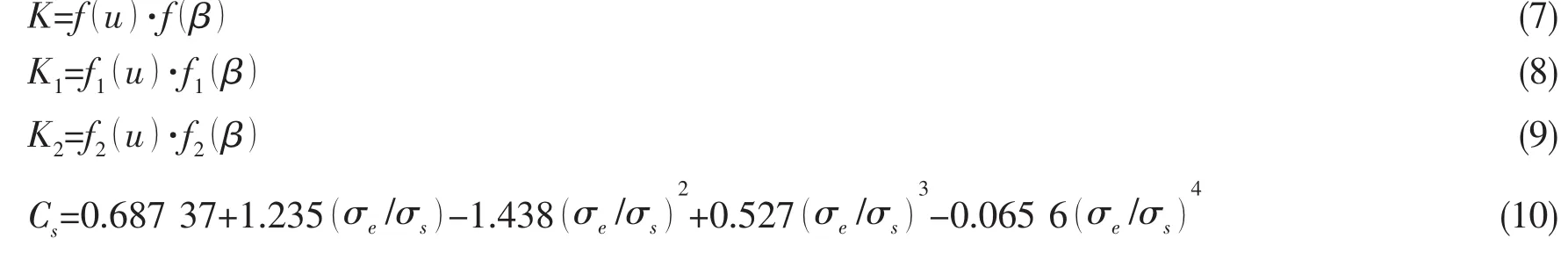
其中：

2.2 扁球封头优化设计

救生舱的上下封头为受外压扁球封头。根据规范要求，需满足强度和稳定性两项要求，即：

Cs、Cz和 C 回归结果如下：

（11）式可将（12）～（14）式代入后进行迭代计算，寻找最优化厚度。

2.3 开孔加强设计

舱口盖开口加强通常有两种方法，一种方法是采用法兰加强形式，一种是采用围栏加强形式。对围栏加强时，可采用变截面围栏。对于本结构采用围栏加强更加有利，原因是法兰下封头的壳体厚度较薄，与法兰连接过渡区域较大，围栏加强结构形式更加简单。

采用围栏加强时，开口加强的面积为：

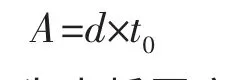
其中t0为壳板厚度，若围栏厚度为t1，则有效高度为：

围壁所需厚度为t2：

有效宽度：

壳体有效加强面积为三部分之和：

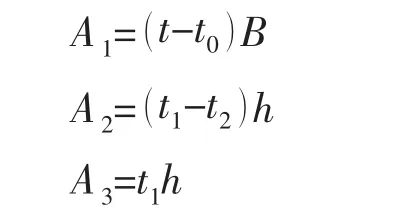
要求:

即f （t1）≥A/2，可满意设计。

本文编织程序，采用搜索法获取最小t1。

2.4 优化设计算例

表1 基本设计参数Tab.1 The basic design parameters

通过程序计算，环肋圆柱体的第一次优化结果见表2。

表2 第一优化计算结果Tab.2 First optimum results

从表2可以看到，各应力、失稳压力均接近规范规定许用值，浮重比达7.5。该计算结果可认为是最优承载结构尺寸。根据工程设计中总体布置的需要，肋骨间距实际取值为420 mm，在此基础上，可做第二次优化计算。计算结果见表3。

表3 第二优化计算结果Tab.3 Second optimum results

从表3看到，受肋骨间距非最优化的影响，各应力比最优值显著降低，失稳压力和总重量增加，浮重比降至5.96。本结构最终工程取值为壳板厚度10 mm。肋骨选用面板6×30 mm，腹板5×250的T型材代替。其浮重比为4.98。

程序计算得到的出入舱口开口围栏最优尺寸为：

有效高度h＝167 mm

实际取值为 t1＝24 mm，h＝175 mm。

根据程序计算结果，上封头和下封头的最优厚度为16.1 mm，实际取值为18 mm。

3 试验分析

图1 舱口盖开口围栏贴片图Fig.1 Strain gauge distribution near hatch enclosure

图2 封头和环肋圆柱壳体体贴片图Fig.2 Strain gauge distribution of ring-strengthen shell and spherical envelop

通过以上设计确定的结构尺寸，进行了救生舱建造。在压力筒内对实物进行了耐压试压。耐压试验的最高压力为工作深度的1.25倍，即2.5 MPa。图1是出入舱口围栏应变片分布图。图2是封头和环肋圆柱壳应变片分布图。图3是环肋圆柱壳体典型应力点的应变随压力变化曲线。表4是对典型应力程序计算结果和试压结果的比较。比较结果表明，试验与程序计算比较接近。从该表中也可以看出，试验和计算应力均远低于许用值。这是由于受总体布置等因素的约束，实际设计尺寸的浮重比为4.98，远低于最佳承载结构尺寸浮重比7.5。

图3 典型应力点的应变—试验压力曲线Fig.3 Strain-test pressure for typical stress locations

表4 试验应力与计算应力的比较Tab.3 Comparison between calculation results and test results

4 结 论

本文针对救生舱的耐压结构进行了优化分析，在满足规范要求的基础上，开发了一套优化设计程序，用于寻找最优结构尺寸。在此基础之上，本文设计了一只救生舱结构。对设计的救生舱进行了耐压试验考核验证，获得了典型部位的应力应变分布。对试验结果和计算结果进行了比较分析。通过以上分析证明该优化设计合理，救生舱满足设计要求。

[1]中国船级社.潜水系统和潜水器入级与建造规范[M].北京:人民交通出版社,1996.

[2]ABS.Underwater vehicles,systems and hyperbaric facilites[S].2010.

[3]胡 勇,崔维成.筋对环肋圆柱壳的壳板屈曲强度影响分析[C].全国船舶力学会议,浙江舟山,2005:179-188.