职中数学的教学与教法研究

杨志云

（江都市职业教育集团，江苏 江都 225212）

1 明确教学目标

在教学中，每节课教学目标分为三大领域：①认知领域；②情感领域；③动作领域。因此，在备课时，要围绕教学目标选择教学策略、方法、媒体进行必要的内容重组。在数学教学中要通过师生的共同努力，使学生在知识、能力、技能、心理、思想品德等方面达到预定的目标，以提高学生的综合素质。

2 突出重点，化解难点

每节课都有一个重点，二整堂课教学都要围绕这个重点，逐步深入，是使学生明确重点，老师在上课时要在黑板的一角将内容反映出来（板书或采用实物投影等现代化教具），以引起学生的重视，在讲授重点时，是整个课堂的教学高潮，教师要通过提高声音、手势、板书、幻灯片、电脑课件等直观教具刺激学生大脑，是学生能兴奋起来，对所学的内容留下较深的印象，讲授难点时，要由浅入深（对某些重要的方法要自选或自编习题，促使学生能自觉掌握，联贯运用），在每个等号的后面都要着重说明，从而分散难点，促使学生对新知识的接受。

如：笔者在讲授函数的值域时，采用了常规的教法（观察法、分离常数法、判别式法、图像法等等）之后，选编了如下的一例，对上述的多种方法加以说明，达到了强化的目的，取得了很好的效果。

例：已知 f（x）=x2-4ax2a+30≥0，对一切实数 x 恒成立，确定方程的根的取值范围。

分析：同已知条件f（x）≥0知道，此二次函数的图像在x轴的上方，即与x轴没有交点或只有一个交点，即△≤0（也可以用图像直观表示）。

解：依题意： △=16a2-4（2a+30）≤0

x=a（a+3）=a2+3a，当 a=3，xmax=18；a=1，xmin=4 即 4≤x≤18，而由x=a2+3a知，当a=-时，也有一个极点，但不在1≤a≤3中，所以不予考虑，若万一在此行列中应三者加以比较。

2）当1≤a≤3时，方程为

3 根据内容选择恰当的教法

在教学中，教师应随着教学内容的变化、教学设备的变化，灵活选用教学方法。教学方法很多，对于新授课，我们可以采用“引导探索”的教法，有时在一节课上要用多种教学方法。俗话说“教无定法，贵在得法。”如在每章节的开始，数学课总少不了概念课，对此有些“可爱”的学生提出质疑：“数学又不是法律，要那么多的条条框框干什么，无味……”一句话提出，看气氛，赞同的还不在少数，课后，我改变了原来的教学计划，列举了部分说明概念的重要性。如：

例子1，设x1、x2是方程ax2+bx+c=0的两个根，若s1=x1+x2，s2=x12+x22，s3=x13+x23，证明：as3+bs2+cs1=0。

分析：本题要求证明 a（x13+x23）+b（x12+x22）+c（x1+x2）=0，先由学生做，大多数想到的是跟与系数的关系式定理。

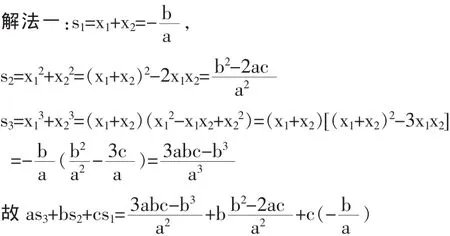
解法二：由定义知：x1、x2是方程ax2+bx+c=0的两个根

∴ax12+bx1+c=0，ax22+bx2+c=0

即 as3+bs2+cs1=a（x13+x23）+b（x12+x22）+c（x1+x2）

=（ax12+bx1+c）x1+（ax22+bx2+c）x2=0

例 2、已知 2a2-2a+k=0，2b2-2b+k=0，且 a-b=2，求 k 的值。

一般解法是：由2a2-2a+k=0与2b2-2b+k=0这两式相减，2（a2-b2）-2（a-b）=0 即（a-b）（a+b-1），由题意知 a≠b，故 a+b=1与a-b=2联立方程组得

如果认真观察题设，不难看出a，b是方程ax2+bx+c=0的两个根，故a+b=1与a-b=2联立方程组可得，以下同上（略）

当然还可以举出更多的例题充分说明定义、定理、公式和法则是解题的依据或捷径，但利用定义解题往往会被人忽视，某些问题根据定义解题比其他方法奏效。

笔者通过两种方法比较说明：第一种方法属于通常解法，代入2a2-2a+k=0得是容易想到的，但运用起来比较繁琐；第二种方法显得思路清晰，方法新颖，运用简捷，现将我们通过实践证明认为效果较好的教法（教学模式）分类整理归纳如下。

教学模式 教学过程传递-授受（传统式）复习旧知识-授新知识-巩固应用-总结评价-布置作业综合教学 论-做-议-讲-练引导探索 提出问题-启发引导-实验探索-谈论分析-概括总结-实际应用（布置作业）自学辅导 明确要求-自学质疑-讨论启发-练习应用-总结评价

4 注意调整课堂的教学

教学过程中，老师要随时了解学生所学的内容，掌握情况，从学生的一举一动、一笑一叫中得到信息的反馈，并认真分析心理。如果学生思维畅通，教师就可以加快速度，可适当的加深、加宽、加点补充材料，让学生进入“临近发展区”，“跳一跳摘得到”。若学生思维受阻，教师在应用现有的教材的基础上，搜集些古往今来的，与其有关的趣味与笑话，还可以采用现代化的教学方法，如实物投影、幻灯片、电脑课件等，这样就可以随时随地、自觉不自觉地引起他们的注意和思考，甚至可使他们忘记生理和心理上的巨大痛苦，以百倍的勤奋、百折不挠的毅力去研究它，以达到清楚地理解，从而对数学产生更大的兴趣，使他们知道，职中的教学与教法就是与普中不同。