基于BP神经网络工具箱实现函数逼近

王丽萍

（长安大学，陕西 西安 710054）

1 BP神经网络的结构

BP神经网络，通常由输入层、输出层和隐含层构成，相邻层节点之间通过权连接，同层神经元之间没有联系，每一层神经元的状态只影响下一层的神经元的输入和输出。

根据Kolmogorov定理，在隐层使用S形传输函数，在输出层中使用线形传输函数的三层神经网络，几乎可以以任意精度逼近任何连续函数，只要隐层中有足够的单元可用。隐含层节点数的选取至今没有确切的方法和理论，一般情况下根据学习样本和测试样本误差的学习和修改来选取的。通常情况下隐含层神经元个数太少，网络所能获取的用来解决问题的信息太少；隐含层神经元个数太多，使得训练时间增大，不能够在人们接受的时间内完成训练，更重要是隐含层神经元过多，可能引起所谓的“过拟合”现象，即把网络训练集里一些无关紧要、非本质的东西也学会。一个典型的3层BP神经网络模型结构如图1所示。

2 BP神经网络的学习算法

BP算法的基本思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输入层传入,经隐含层处理后,传向输出层。若输出层的实际输出与期望的输出不符,则转入误差的反向传播阶段。误差反传是将输出误差以某种形式通过隐层向输入层逐层反传将误差信号沿原来的神经元连接通路返回，返回过程中逐一修改各层神经元连接的权值。

学习步骤如下：

设BP网络的输入层、隐含层和输出层分别有I、J和K个神经元，

输入层第i个神经元的输入和输入层第i个神经元的输出分别为：xi和 oi；

隐含层第j个神经元的输入：

图1 3层BP神经网络模型结构图

式中，wij为输入层中第i个神经元到隐含层第j个神经元的权值，θj为隐含层第j个神经元的阈值；

隐含层第j个神经元的输出：

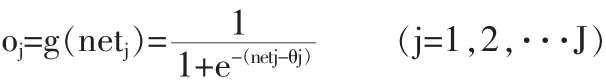
其中g( )为正切S型传递函数；

式中，wkj为隐含层中第j个神经元到输出层第k个神经元的权值，θk为输出层第k个神经元的阈值；输出层第k个神经元的输出：ok=g（netk）=netk（k=1，2，···k），其中 g( )为线性传输函数；

BP网络的学习过程按使误差函数减小最快的方向调整加权系数，目标是使网络输出与训练样本的均方误差最小。

设训练样本为 P 个，输入向量为 x1，x2，···xp，实际输出向量为 o1，o2，···op，期望的输出向量为 t1，t2，···tp。

输出层神经元系数的修正公式：

△wkj=ηδpkopj=ηopj（tpk-okp）（1-okp）okp

隐含层权系数的调整：

η为学习率。

3 MATLAB神经网络工具箱

MATLAB神经网络工具箱以人工神经网络为基础，根据自己的需要调用相关函数，就可以完成网络设计、权值初始化、网络训练等，MATLAB神经网络工具箱包括的网络有感知器、线性网络、BP神经网络、径向基网络、自组织网络和回归网络，BP神经网络工具箱主要包括newff，sim和train三个神经网络函数。

（1）newff：BP 神经网络参数设置函数

函数功能：构建一个BP神经网络。

函 数 形 式 ：net= newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)

P：输入数据矩阵

T：输出数据矩阵

S：隐含层节点数

TF：节点传递函数，包括硬限幅传递函数hardlim，对称硬限幅传递函数hardlims，线性传递函数purelin，正切S型传递函数tansig，对数S型传递函数logsig

BTF：训练函数，包括梯度下降BP算法训练函数traingd，动量反传的梯度下降BP算法训练函数traingdm，动态自适应学习率的梯度下降BP算法训练函数traingda，动量反传和动态自适应学习率的梯度下降BP算法训练函数traingdx，Levenberg_Marquardt的BP算法训练函数trainlm

BLF：网络学习函数，包括BP学习规则learngd，带动量项的BP学习规则learngdm

PF：性能分析函数，包括均值绝对误差性能分析函数mae，均方差性能分析函数mse

IPF：输入处理函数

OPF：输出处理函数

DDF：验证数据划分函数

一般在使用过程中设置前六个参数，后四个参数采用系统默认参数。

（2）train：BP 神经网络训练函数

函数功能：用训练数据训练BP神经网络。

函数形式：[net,tr]=train(NET,X,T,Pi,Ai)

NET：待训练网络

X：输入数据矩阵

T：输出数据矩阵

Pi：初始化输入层条件

Ai：初始化输出层条件

net：训练好的网络

tr：训练过程记录

一般在使用过程中设置前三个参数，后两个参数采用系统默认参数。

（3）sim：BP 神经网络预测函数

函数功能：用训练好的BP神经网络预测函数输出

函数形式：y=sim(net,x)

net：训练好的网络

x：输入数据

y：网络预测数据

4 用MATLAB神经网络工具箱进行函数逼近

设要逼近的非线性函数为：

y=8+2*exp(1-x.^2).*cos(2*pi*x)，-0.4

（1）网络建立：使用net=newff(x,y,20,{'tansig','purelin'},'trainlm','learngdm');语句建立一个前馈BP神经网络。该BP神经网络只含有一个隐含层，神经元的个数为20，隐层传递函数tansig，输出层传递函数purelin，训练函数为Levenberg_Marquardt的BP算法训练函数trainlm，网络学习函数是带动量项的BP学习规则learngdm。

（2）网络训练：使用net=train(net,x,y);语句训练建立喊的BP神经网络。在训练网络之前设置好训练参数。

用“net.trainParam.epochs=50;net.trainParam.goal=0.01;net.train-Param.lr=0.01;

net.trainParam.show=10;”语句实现。其他参数默认。

（3）网络仿真：使用“y1=sim(net,x);y2=sim(net,x);”语句仿真训练前后的BP神经网络。

程序1：MATLAB程序源代码

x=[-0.4:0.04:3.6];

y=8+2*exp(1-x.^2).*cos(2*pi*x);

net=newff(x,y,20,{'tansig','purelin'},'trainlm','learngdm');

y1=sim(net,x);%未训练前进行仿真

net.trainParam.epochs=50;

net.trainParam.goal=0.01;

net.trainParam.lr=0.01;

net.trainParam.show=10;

net=train(net,x,y); %训练函数

y2=sim(net,x);

figure(1)

>>plot(x,y,'-',x,y1,'--',x,y2,'+')

title('原函数与网络训练前后的仿真结果比较')

>>xlabel('x');ylabel('y')

>>text(2,33,'-原函数y')

>>text(2,30,'--未训练网络的仿真结果y1')

>>text(2,27,'+训练网络的仿真结果y2')

原函数与网络训练前后的仿真结果比较

图2 原函数与网络训练前后的仿真结果比较

图3 训练误差

由程序知直接调用MATLAB软件包中的神经网络工具箱函数。图2为原函数与网络训练前后的仿真结果比较图。由图可知，用工具箱函数建立网络时，对权值和阈值的初始化是随机的，所以未训练网络的仿真效果很差，并且每次运行结果也不同。训练后网络的仿真输出曲线和原函数的曲线非常接近，这说明训练后的网络对非线性函数的逼近效果很好。网络训练过程中误差随训练时间的变化迅速减少，在经过4个单位时间以后，网络的误差就达到了逼近要求（图3）。

5 结论

Matlab软件包中的BP工具箱函数在数学计算、图形计算、计算机仿真等方面为研究和设计神经网络提供了便利的工具,BP神经网络最强大的应用之一就是函数逼近。BP工具箱函数克服了计算机高级语言编程的复杂性问题,语言简单,调试方便,程序运行效率极高,具有重要的推广应用前景.

[1]王伟.人工神经网络原理入门及应用[M].北京:北京航空航天大学出社，1995.

[2]李国勇.神经网络控制及其Matlab实现[M].北京:电子工业出版社，2005.

[3]周开利,康耀红.神经网路模型及其Matlab仿真程序设计[M].北京:清华大学出版社，2005.

[4]飞思科技产品研发中心.神经网络理论与Matlab7实现[M].北京:电子工业出版社，2005.

[5]丛爽.面向MATLAB工具箱的神经网络理论与应用[M].合肥:中国科学技术大学出版社，1998.

[6]闻新，周露，等.Matlab神经网络应用设计[M].北京:科学出版社，2001.

[7]闵惜琳，刘国华.用MATLAB神经网络工具箱开发BP网络应用[J].计算机应用，2001，21(8):163-164.