基于采样点卡尔曼滤波的动力电池SOC估计

高明煜 何志伟 徐 杰

（1.武汉理工大学信息工程学院 武汉 430070 2.杭州电子科技大学电子信息学院 杭州 310018）

1 引言

电池作为备用电源已在通信、电力系统、军事装备、电动汽车等领域得到了广泛的应用。随着环保观念的日渐深入人心，越来越多的系统开始采用电池作为主要动力供给。在这些系统中，动力电池工作状态的好坏直接关系到整个系统的运行可靠性。为确保动力电池组的性能良好，延长电池组使用寿命，须及时、准确地了解电池的运行状态，对电池进行合理有效的管理和控制。而在电池各运行状态如电池荷电状态（State of Charge，SOC）、功率衰落、容量衰落等参数中，电池的SOC参数最为重要，其精确估算是电池能量管理系统中最核心的技术，通过SOC和其他一些相关量的变化，可以判断出电池组中各单体电池的当前状态，决定是否需要进行电池均衡或更换某一单体电池，而不影响整个电池组的整体性能[1]。SOC的作用与燃油汽车系统中的油量表类似，但是，剩余油量可以通过相应的传感器直接测得，而电池的SOC却无法用一种传感器直接测得，它必须通过对一些其他物理量的测量并采用一定的数学模型和算法来估计得到。

一般来说，与电池的SOC有着密切关系的物理量包括电池的端电压、工作电流、电池内阻及其周围环境温度等。基于这些物理量，目前，对单体电池SOC估计的主要方法有开路电压法[2]、内阻法[3]、安时法[4]等。开路电压法进行电池SOC估计时电池必须静置较长时间以达到稳定状态，而且只适用于电池电流非剧烈变化状态下的SOC估计，不能满足在线检测要求。内阻法需要精确测量电池的内阻，由于一般电池内阻在毫欧级，因此对测量仪器的要求非常高，难以在实际中加以应用。安时法易受到电流测量精度的影响，在高温或电流波动剧烈情况下，精度很差。

为了达到更高的SOC估计准确度，目前，国内外对于动态系统中电池SOC的估计采用较多的一种方法是神经网络法[5-6]。神经网络具有非线性的基本特性，同时具有并行结构和学习能力。当网络训练完成以后，对于给定的外部激励，能直接给出相应的输出。利用这样的特点，神经网络法以工作电压、工作温度、充放电倍率等作为输入，以SOC为输出来模拟电池的动态特性，最终达到估计SOC的目的。但是，神经网络输入变量的选择是否合适，变量数量是否恰当，直接影响模型的准确性和计算量；而且需要大量的参考数据进行训练，估计误差受训练数据和训练方法的影响很大。如果用于网络训练的数据不准确或者不完备则对结果影响很大。另外，动力电池工作时，其状态具有非常大的动态性，另一方面，即使同一批电池，其内部参数也不完全一致，因此，采用同种训练参数来适用于不同的电池，效果可能会不理想。

当将电池看作一个动态系统时，卡尔曼滤波方法可以对动态系统的状态做出最小均方意义上的最优估计。卡尔曼滤波已经在目标跟踪、全局定位、动态系统控制、导航、通信等领域有了广泛的应用。卡尔曼滤波方法在电池SOC估计领域的应用研究也越来越受到关注[7]。当采用卡尔曼滤波进行电池SOC估计时，可以将电池SOC看作是系统内部状态向量的一个分量。但是，卡尔曼滤波只能对线性系统进行建模，而电池系统往往比较复杂，采用线性系统对电池进行建模得到的SOC估计精度必定受到限制。这一问题的解决办法之一是采用扩展卡尔曼滤波来进行SOC的估计，并取得了不错的研究结果[8]。但是，EKF为了求取估计误差方差通过非线性函数的传播，需将非线性函数用Taylor级数展开并线性化，一方面增加了计算复杂度，另一方面，在该过程中忽略了高阶项，必定会引起误差。

本文提出将卡尔曼滤波的另一种新推广方法——采样点卡尔曼滤波应用到电池SOC估计中。与扩展卡尔曼滤波不同的是，它通过设计少量的采样点，根据采样点经由非线性函数的传播，计算出随机向量一、二阶统计特性的传播。因此，它比扩展卡尔曼滤波能更好地逼近方程的非线性特性，从而比扩展卡尔曼滤波具有更高的估计精度。首先，文中给出了进行动力电池SOC估计的模型，从而描述电流、电压、温度与其SOC之间的非线性关系；然后，给出了针对该模型利用采样点卡尔曼滤波进行电池SOC估计的关键步骤和算法；进而在实验中对算法的估计精度、鲁棒性及复杂度进行了验证。

2 动力电池SOC估计模型

电池动态系统中的状态变量除了电池SOC外，还可以有很多种，但为了简单起见，本文暂只考虑以电池SOC作为主要的状态变量，并主要考虑放电电流、端电压、工作温度与电池SOC间的关系。

2.1 过程模型

电池的SOC又称电池剩余电量，指的是电池内所剩的容量（安时数）占标称容量（安时数）的百分比，其中标称容量指电池完全充满后在室温下以标准放电速率C/30（C为额定放电电流）进行放电时所能得到的总容量。因此，电池t在时刻的剩余电量z(t) 可以表示为

式中η——放电比例系数，与放电速度、温度等有关；

Qn——电池的标称容量；

i(τ)——电池在τ时刻的即时放电电流。

为了应用卡尔曼方法进行递推估计，上述方程（1）可以离散化为

式中 Δt——离散时间间隔。

在本文中，只考虑放电电流和工作温度对电池SOC的影响，因此，取η=ηi/ηT，其中ηi反映的是放电速率（电流）对电池SOC的影响程度，即室温下放电电流为i时的放电比例系数（在标准放电速率下即i=C/30时，ηi=1）；ηT反映的是电池工作温度对电池SOC的影响程度，即工作温度为T、放电电流为C/30时的放电比例系数（在室温即T=25℃时ηT=1）。图1和图2分别给出了某标称容量为15A·h的磷酸铁锂电池，其不同放电速率及工作温度对电池SOC的影响程度。从图中可以看出，在电池允许工作范围内，电池放电速率越高，总放电容量越低；工作温度越高，总放电容量越高。

图1 不同放电速率下的电池容量Fig.1 Battery capacity under different discharge rates

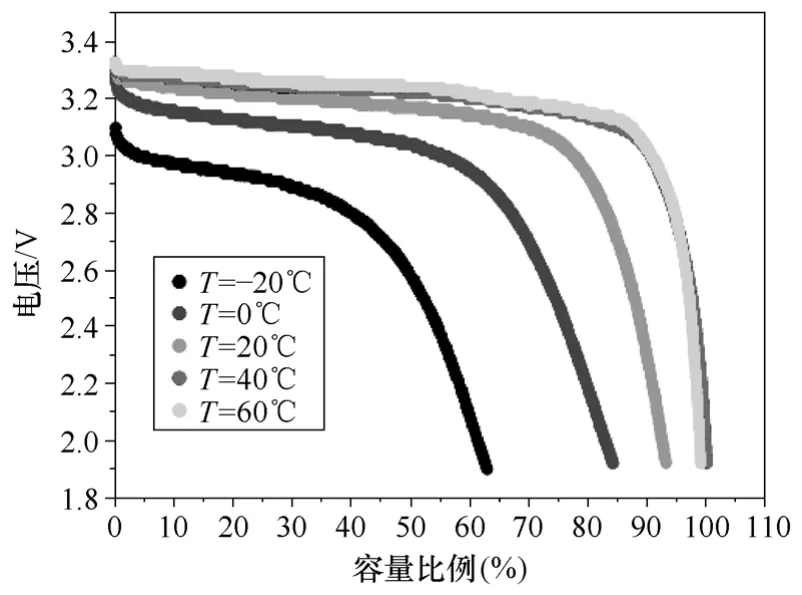
图2 不同温度下所能得到的电池容量比例Fig.2 The ratios of drawn capacity under different temperatures

本文中，ηi和ηT的确定方法分别为：

（2）根据电池在不同工作温度Tk下所能得到的电池容量比例rk，根据最小二乘法在最小均方误差准则下拟合出如下二次曲线：其中p，q，s为所求得的最优系数，则当工作温度为T时

2.2 观测模型

电池的端电压与电池的SOC满足一定的关系，因此，当SOC作为模型状态已知后，电池端电压也可以据此预测出来。在文献[9]中给出了其中的几个模型，分别如下。

Shepherd模型

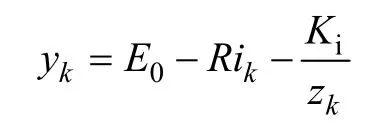
Unnewehr通用模型

Nernst模型

在这些模型中，yk是电池端电压，ik是放电电流，zk是电池SOC，R是电池内阻，Ki是极化电阻，K1～K3是常数。实际上，可以将这些模型结合起来，形成如下的联合观测模型：

令式（3）中的模型参数为矢量p，p=（K0，R，K1，K2，K3，K4）。本文中，p的确定可以由室温下，以标准放电速率对电池进行一次完整放电过程中不同时刻电池端电压yk及对应的电池SOC值，根据最小二乘法拟合得到。

3 基于采样点卡尔曼滤波的电池SOC估计

3.1 采样点卡尔曼滤波

考虑非线性系统：

式中xk——k时刻系统的L维状态矢量；

uk——控制输入矢量；

yk——系统的观测矢量；

wk，vk——处理噪声及观测噪声。

f与g至少有一个为非线性函数，由于f与g的非线性，无法直接使用卡尔曼滤波来进行系统状态的估计。一种常用方法是将它们用Taylor级数进行展开并取其一阶线性量对原函数进行线性近似后再采用卡尔曼滤波进行估计，即采用扩展卡尔曼滤波完成该非线性系统的状态估计过程，这一过程存在两个缺点：①当非线性函数的Taylor 展开式高阶项无法忽略时，线性化会使系统产生较大误差，甚至使滤波器不稳定。②在每个滤波周期需要计算Jacobian 矩阵，对于复杂高阶系统，将大大增加滤波估计的运算量。采样点卡尔曼滤波器则是另一种迭代型最小均方误差估计器，同扩展卡尔曼滤波一样，它仍属于最优高斯近似卡尔曼滤波器框架中。但与扩展卡尔曼滤波器不同的是，采样点卡尔曼滤波器并不直接对过程模型和观测模型进行线性近似，而是利用实际的非线性模型对状态变量的分布进行近似[10]。在采样点卡尔曼滤波中，首先由k-1时刻状态的最优估计xˆk-1，按照一定的分布构建出2L+1个采样点，并赋予每个采样点对应的权值，因此这些采样点完全拥有状态变量的均值和协方差信息。系统的状态估计及观测估计是这些采样点通过实际非线性系统传播后的加权结果。最终直接根据卡尔曼滤波过程对状态估计及观测估计进行更新，完成整个滤波过程。S.J.Juliear等[11]的研究表明：采用这一过程，任何非线性系统的后验均值和协方差都可以精确到Taylor级数展开式中的二阶量，从而使误差只存在于三阶及以上。因此，与扩展卡尔曼滤波相比：采样点卡尔曼滤波器具有更高的估计精度，且无需计算复杂的Jacobian矩阵，体现出很好的优越性。

3.2 基于采样点卡尔曼滤波的电池SOC估计

从前文所述动力电池观测模型表达式（3）可知，动力电池是一个复杂的非线性系统。由于放电电流ik及电池端电压yk不可避免地存在测量误差，另一方面，所拟合得到的相关模型也不可能完全准确地描述复杂的电池动态系统，因此，利用采样点卡尔曼滤波从统计角度对这些不确定性进行处理可能会取得更好的结果。在过程模型和观测模型中分别加入处理噪声项wk及观测噪声项vk，从而形成如式（4）所示的处理方程及式（5）所示的观测方程：

现假定处理噪声wk的方差为Rw，观测噪声vk的方差为Rv，其中Rw与电流测量误差有密切关系，Rv与电压测量误差有密切关系。

基于上述处理方程及观测方程，采用采样点卡尔曼滤波进行电池SOC估计的具体步骤如下：

（1）初始化：设定电池初始SOC为zˆ0，其估计方差为P0，确定合适的Rw及Rv值。

（2）考虑到处理噪声和观测噪声的影响，将状态变量zk-1及其估计方差Pk-1分别进行如下扩展，得到扩展状态变量xk及其协方差Pkx为

扩展状态变量xk的维度为L=3。

（3）根据测量得到的电池端电压yk及放电电流ik，k=1,2,…，按照如下过程进行递推计算。

①计算加权采样点序列

其中，采样点为

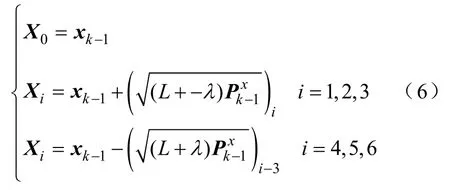
加权系数为

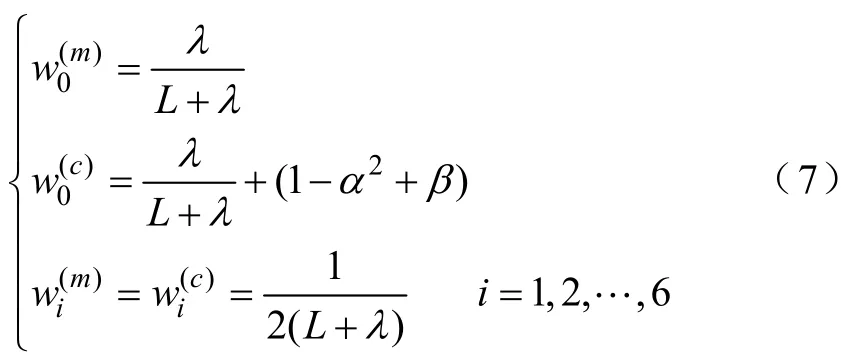
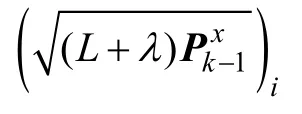
②由采样点，根据处理方程（4）计算状态更新

计算采样点更新Xk|k-1

计算状态估计

计算估计状态的协方差

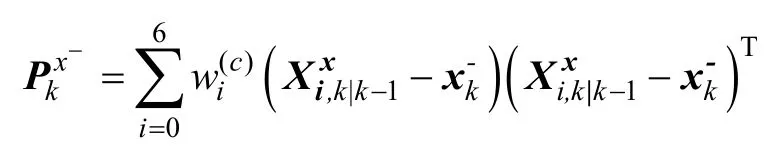
③根据观测方程计算测量更新：

计算测量更新Yk|k-1

计算测量估计yk-

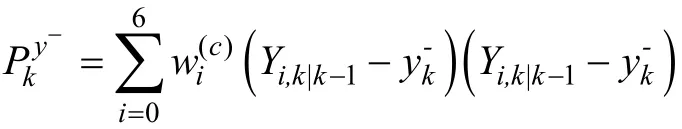
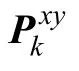
计算卡尔曼增益Kk

计算更新状态xk

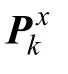
按照上述迭代过程得到的更新状态xk的第一个分量即为k时刻的电池SOC的估计值，的第一个分量则为该估计值的估计方差。因此，采用采样点卡尔曼滤波算法在得到SOC估计值的同时，还可以从其估计方差得到该估计的准确程度。

4 实验分析

4.1 实验数据获取

实验数据通过锂电池试验平台获得，试验平台由可编程直流电子负载模块、数据采集模块、锂电池保护模块、充电模块构成。试验中测试所用电池为浙江万向电动汽车有限公司生产的用于电动汽车的磷酸铁锂电池，电池标准电压为3.3V，标称容量为15A·h。电池放电过程遵循电动汽车性能测试中广泛使用的UDDS模拟行程，利用可编程直流电子负载模拟车辆在城市道路行驶时所需求的负载功率。使用高精度电压、电流和温度采样设备记录锂电池的相关工况，采样频率为1Hz。

图3显示的是某一测试过程中所获得的各采样值，其中，为了使图形更清晰，电流值只给出了一部分，从图中可以看出，放电过程中电流变化非常剧烈。图中放电过程中各个时刻的SOC数值是通过计算锂电池放电到截止电压时所释放的总电量，然后用此总电量作为基准计算得到的；在测试过程中电池温度基本保持不变。

图3 锂电池的放电电流、端电压与实际SOCFig.3 The measured currency,terminal voltage and real SOC of a lithium-ion battery

4.2 实验结果

根据图3中实际测量得到的电池放电电流及端电压，应用本文中基于采样点卡尔曼滤波方法进行电动汽车锂电池的SOC估计结果及误差曲线如图4所示。为便于比较，图5给出了采用扩展卡尔曼滤波进行SOC估计及估计误差曲线。

两种方法所使用的各参数一致，分别为

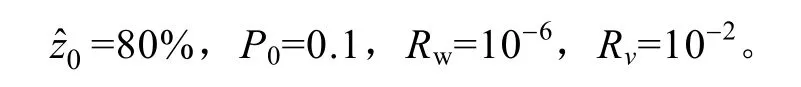
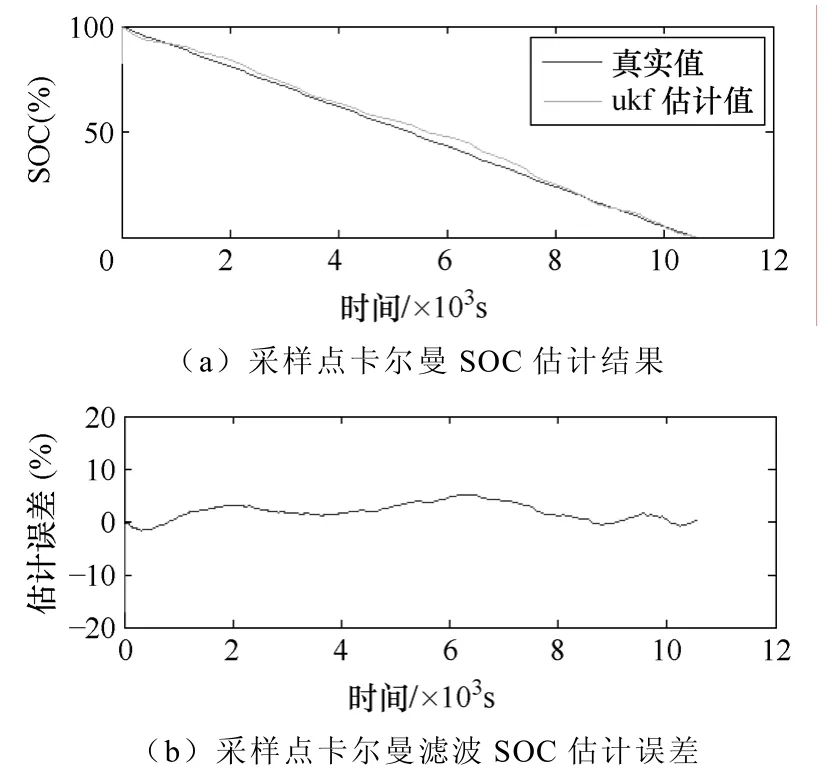
图4 采样点卡尔曼滤波进行SOC估计Fig.4 Results of SOC estimation based on sigma point Kalman filter

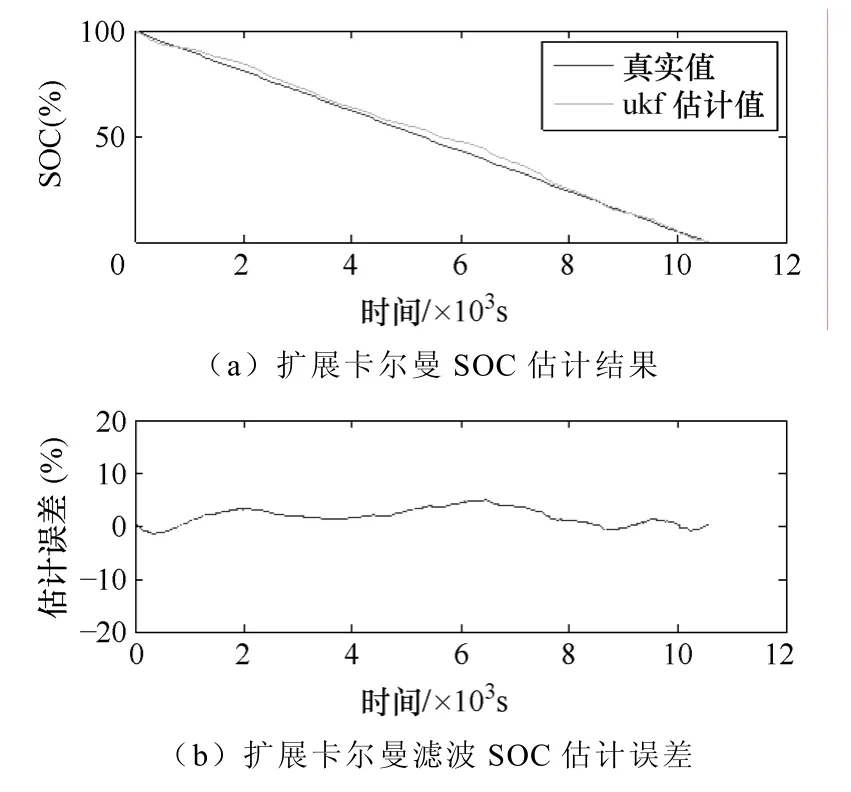
图5 扩展卡尔曼滤波进行SOC估计Fig.5 Result of SOC estimation based on extended Kalman filter

从图4中可看出，虽然算法选定的初始SOC值与真实SOC存在一定偏差，但算法能快速地跟踪上真实SOC值。下表中给出了采样点卡尔曼滤波和扩展卡尔曼滤波两种不同滤波方法性能比较。

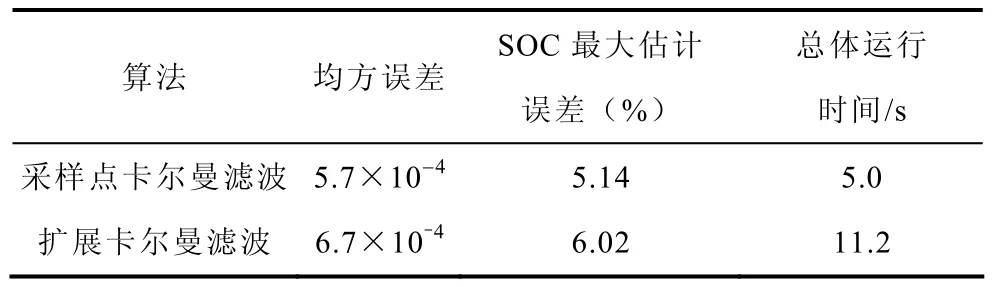
表 算法性能比较Tab.Performance comparison

从实验结果可知，采样点卡尔曼滤波方法不论是均方误差还是最大误差均比扩展卡尔曼滤波要小，具有更高的估计精度，速度比相应的扩展卡尔曼滤波要快1倍以上，其最大误差只有5.14%，完全可以满足实际应用的要求。

图6给出了在不同初始状态估计方差P0情况下电池SOC估计的过程。从图6可看出，随着P0的不断增加，收敛速度会加快，但并不表明P0越大越好，P0比较合适的值应为1～12附近。

图6 P0的选取对算法收敛速度的影响Fig.6 P0 Influence of P0 to the convergence rate

为进一步研究观测模型参数改变对SOC估计的影响，将其修改为p2=[3.3619 -0.0039 0.0001-0.0924 0.0903 -0.0129]，应用到同样的测试数据后，电池SOC估计过程的对比结果如图7所示。从图7可看出，本文算法可以很好地适应观测模型参数的微小变化，对于同类型的不同电池，即使其内部参数存在着一定的差异，仍可以采用同一套模型参数来进行其SOC的精确估计。

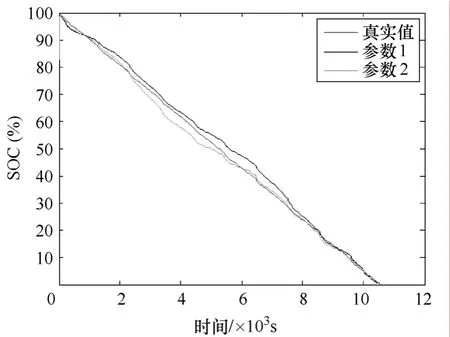
图7 观测模型参数微调对SOC估计的影响Fig.7 Influence of a small adjustment to the parameters of the measurement model

5 结论

本文详细描述了利用采样点卡尔曼滤波算法进行动力电池SOC估计的方法和过程，探讨了如何对电池过程模型进行修改，使其适应不同的温度条件及不同的放电速率。与传统卡尔曼滤波和扩展卡尔曼滤波相比，采样点卡尔曼滤波利用一系列拥有状态变量均值和方差信息的采样点经由非线性系统传播，直接得到电池荷电状态的估计及其估计方差，在避免复杂的求导运算的同时进一步提高了SOC的估计精度。实验表明：采样点卡尔曼滤波算法可以用来进行动力电池SOC的快速精确估计，最大误差在5%左右；模型参数的微小变化不影响SOC的估计精度，可以方便地应用于同种类型不同电池中。

[1] 李槟,陈全世.混合动力电动汽车中电池特性的研究[J].汽车技术,1999(10): 11-14.

[2] Aylor J H,Thieme A,Johnson B W.A battery state of charge indicator for electric wheelchairs[J].IEEE Transactions on Industrial Electronics,1992,39(10): 398-409.

[3] 高明裕,张红岩.蓄电池剩余电量在线测量[J].电测与仪表,2000,37(9): 28-31.Gao Mingyu,Zhang Hongyan.Online measurement of battery remaining capacity[J].Electrical Measurement &Instrumentation,2000,37(9): 28-31.

[4] 李申飞,易菊兰,琚小明.电池电量精确测量方法的研究与实现[J].计算机工程与应用,2009,47(17):244-248.Li Shenfei,Yi Julan,Ju Xiaoming.Research and implementation on accurate measurement of battery capacity[J].Computer Engineering and Applications,2009,47(17): 244-248.

[5] 雷肖,陈清泉,刘开培,等.电动车电池SOC估计的径向基函数神经网络方法[J].电工技术学报,2008,23(5): 81-87.Lei Xiao,Chan C C,Liu Kaipei,et al.Radial-basedfunction neural network based SOC estimation for electric vehicles[J].Transactions of China Electrotechnical Society,2008,23(5): 81-87.

[6] Tsutomu Y,Kazuaki S,Ken-Ichiro M.Estimation of the residual capacity of sealed lead-acid batteries by neural network[C].Proceedinds of the 20th International Telecommunications Energy Conference,1998: 210-214.

[7] Gregory L P.Kalman-filter SOC estimation for LIB cells[C].Proceedings of the 19th International Electric Vehicle Symposium,2002: 527-538.

[8] Gregory L Plett.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs Part1.Background [J].Journal of Power Sources,2004,134(2): 252-261.

[9] ThermoAnalytics Inc..Battery modeling for HEV simulation by ThermoAnalytics Inc.http://www.thermoanalytics.com/support/publications/batterymod elsdoc.html

[10] Rudolph van der Merwe,Eric Wan.Sigma-point Kalman filters for probabilistic inference in dynamic state-space models[C].Proceedings of the Workshop on Advances in Machine Learning,2003：1-27.

[11] Julier S J,Uhlmann J K,Durrant Whyte H F.A new approach for filtering nonlinear systems[C].Proceedings of the American Control Conference,Seattle,Washington,1995: 1628-1632.