Plug-In并联式混合动力汽车实时优化能量管理策略

崔纳新 步 刚 吴 剑 符晓玲 张承慧

(1.山东大学控制科学与工程学院 济南 250061 2.山东大学机械工程学院 济南 250061 3.山东政法学院信息科学技术系 济南 250014 4.昌吉学院物理系 昌吉 831100)

1 引言

混合动力汽车既可以改善燃油经济性，也可以降低排放，被认为是近期最有希望替代传统汽车的方案。目前，外接充电式混合动力汽车（Plug-In Hybrid Electric Vehicle，PHEV）受到汽车企业、研究机构和各国政府的普遍关注。PHEV配有可以从外部电网直接充电的高能量密度电池组，有一定的纯电动行驶里程，长距离行驶耗油量低。作为Plug-In并联式混合动力汽车的核心技术之一，能量管理策略的品质直接影响车辆的动力性、经济性和排放性能。

混合动力汽车能量管理策略在电机和发动机两种功率源之间分配功率和转矩输出，以达到最佳燃油经济性，最大限度地减少废气排放，同时保持电池的健康[1]。传统混合动力汽车的能量管理策略可以分为两类[2]：基于规则的能量管理策略和基于优化的能量管理策略。其中，基于规则的能量管理策略又可以分为基于确定性规则的能量管理策略和基于模糊规则的能量管理策略；基于优化的能量管理策略又可分为实时优化能量管理策略和全局最优能量管理策略。

目前关于PHEV能量管理问题的研究刚刚展开，Banvait对基于确定性规则的PHEV能量管理策略进行了研究[3]。基于确定性规则的能量管理策略静态分配转矩，无法获得最优性能，因此，张博、J.Wu等分别采用矩阵分割算法和粒子群算法优化门限参数[4-5]，在一定程度上改进了静态逻辑门限能量管理策略的性能。S.Stockar等基于庞特里亚金最小值原理[6]针对PHEV提出的全局优化策略可以求得控制变量（如发动机/电机转矩）的全局最优解，然而，全局优化策略要求准确知晓整个行驶工况，在实用时具有很大的局限性，其结果一般只能作为能量管理的参考。本文对应用于传统混合动力汽车上的等效燃油消耗最小策略进行改进，提出了适用于PHEV的实时优化能量管理策略。最后，在电动汽车仿真软件ADVISOR平台上进行仿真实验，研究了该能量管理策略对Plug-In并联式混合动力汽车的燃油经济性能的影响。

2 Plug-In并联式混合动力汽车结构

Plug-In并联式混合动力汽车有内燃机和电机两个动力源。他们既可以独立工作，也可共同驱动车辆。当电池电量充足时，优先考虑使用动力电池的电量来驱动电机，实现纯电动模式运行，从而降低排放和油耗；当电池电量不足时，发动机工作并带动电机给电池充电；当需要较大功率驱动时，发动机和电机同时工作。Plug-In并联式混合动力汽车驱动系统结构如图1所示[7-8]。图中，B为蓄电池，E为内燃机，Y为油箱，M为电机，Z为功率转换器，T为传动装置（包括制动、离合器和齿轮箱），P为充电器。

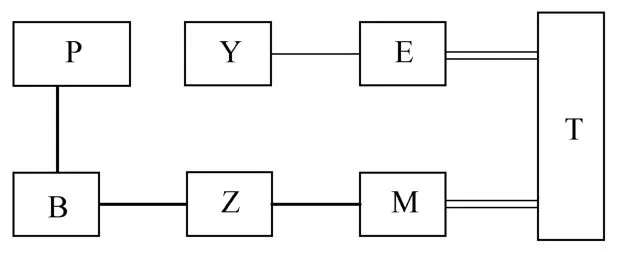
图1 Plug-In并联式混合动力汽车驱动系统结构图—电力连接 —液流连接 =械连接Fig.1 The drive system structure of plug-in parallel hybrid electric vehicle

3 基于确定性规则的能量管理策略

为充分利用电网充入能量，PHEV通常先工作于电量消耗模式（Charge-Depleting，CD），直到电池SOC降低到设定值soc1，才进入电量保持模式（Charge-Sustaining，CS）[9]。当PHEV工作于电量消耗模式时，如果车辆需求功率不大于电机所提供的峰值功率时，发动机关闭，由电机驱动车辆运行；如果车辆需求功率大于电机所提供的峰值功率，起动发动机辅助电机驱动，虽然此时发动机并未运行在高效区，但由于其输出能量很小，故整车燃油消耗仍相对较低[10]。

当PHEV工作于电量保持模式时，最简单的方法是套用传统混合动力汽车的基于确定性规则的能量管理策略，通过判断选定的几个控制变量（驱动系统请求转矩、转速和SOC值）与门限值的关系，决定发动机的启停，并根据预先设定的规则在发动机与电机之间分配转矩，从而使发动机工作在高效区，同时保持SOC位于一定的范围内。

为了制定基于确定性规则的能量管理策略，首先对门限值参数进行说明，见表1。

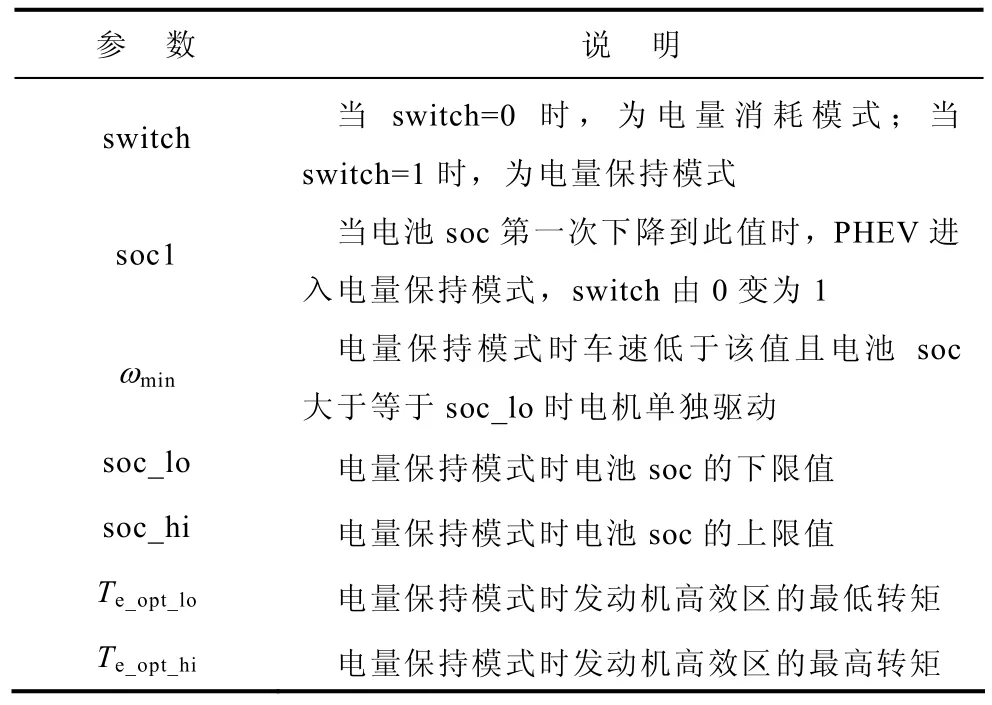
表1 门限值参数说明Tab.1 Threshold parameter description

定义Tr为驱动系统请求转矩，ωr为请求转速，Te为发动机转矩，Tm为电机转矩，Tmc_max为电机在当前速度下的最大转矩，Te_max为发动机在一定速度时的最大转矩，Tchg为电池的充电转矩，Tm_gen_max为电机再生制动的最大转矩。其中，Tchg可以由下式计算

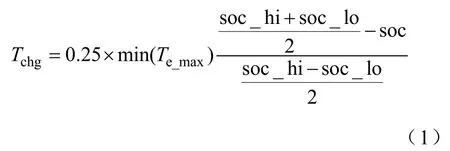
具体的控制规则见表2。

表2 控制规则Tab.2 The control rules

基于确定性规则的能量管理策略简单有效，实用性强，但门限值的确定需要依赖设计人员的过程经验；静态分配转矩，燃油经济性难以达到最优。

4 基于实时优化的能量管理策略

4.1 等效燃油消耗最小原理

等效燃油消耗最小策略是将电机消耗的能量等效成发动机油耗，并与发动机的实际油耗相加，在任一时刻使总油耗最小的算法。该算法能够实现实时优化，不需要路况信息，便于实车应用。

由图1所示PHEV驱动系统，可得如下关系：

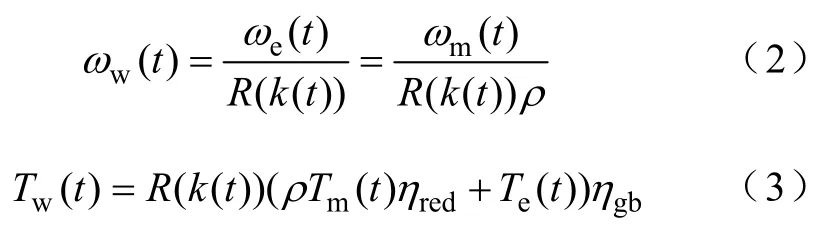
式中ωw(t)，ωe(t)，ωm(t)—车轮、发动机和电机

t时刻的转速；

Tw(t)—车轮需求转矩；

Te(t)，Tm(t)—发动机和电机t时刻的转矩；R(k(t))—k(t)挡的传动比；

ρ—电机减速比；

ηred—电机减速齿轮传动效率；

ηgb—变速箱的传动效率。

机械约束条件如下：

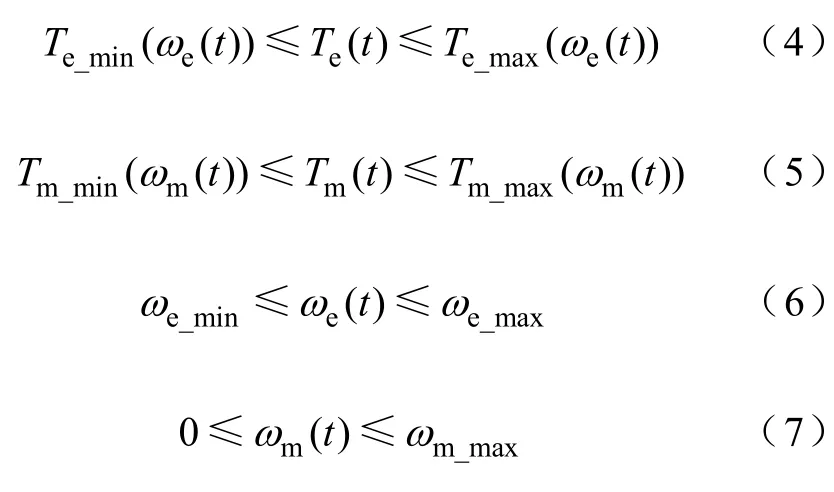
式中

Te_min(ωe(t))，Te_max(ωe(t))—发动机转速为ωe(t)时的最小和最大转矩；

Tm_min(ωm(t))，Tm_max(ωm(t))—电机转速为ωm(t)时的最小和最大转矩；

ωe_min，ωe_max—发动机转速的最小和最大值；

ωm_max—电机转速的最大值。

发动机t时刻的燃油率为Me(Te(t)，ωe(t))，电池t时刻吸收或释放的能量由式（8）转换成燃油率

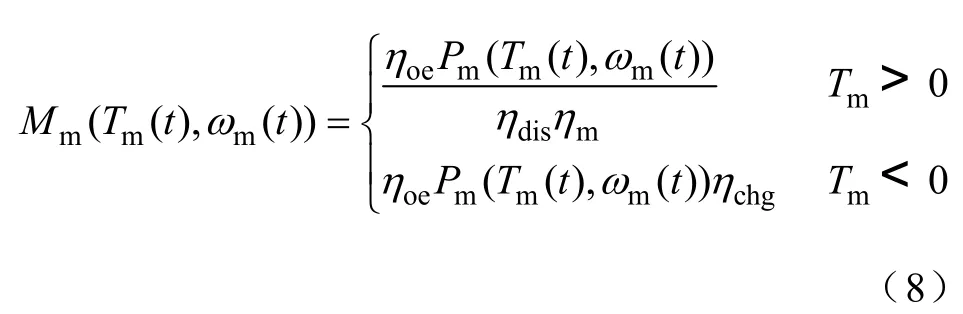
式中Pm(Tm(t)，ωm(t))—电机的功率；

ηdis，ηchg—电池的放电、充电效率；

ηm—电机的平均效率；

ηoe—油-电平均转换效率，可表示为

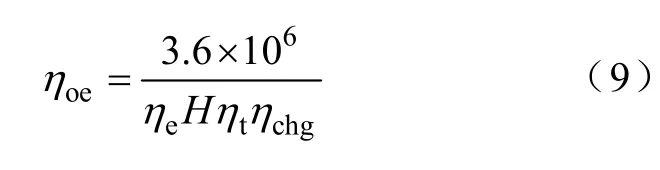
式中ηe—发动机平均效率；

H—燃油的热值；

ηt—油-电转换支路的机械传动效率平均值。

t时刻，总的燃油消耗率为

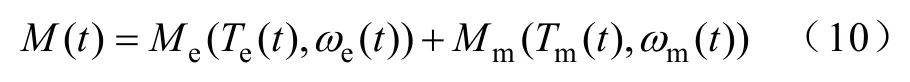
等效燃油消耗最小就是使t时刻总的燃油消耗率最小，即

4.2 电池能量观测单元

等效燃油消耗最小策略原是针对传统混合动力汽车提出的。传统混合动力汽车利用发动机带动电机对电池充电，也就是油转变为电存储在电池中，但PHEV电池中的电能大部分来源于外部电网。为计算PHEV的燃油经济性，需区分动力电池中来自电网的电能和来自燃油的电能。由于在电量保持阶段电池SOC上下波动，因此不能利用SOC来判断来自电网的电量是否已经耗尽。故本文设计了电池能量观测单元，电池能量观测单元的输出值是电池放出的能量累积和，其原理如图2所示。图中，P为电池放电功率，T为工作周期时间，Eout为总能量输出。

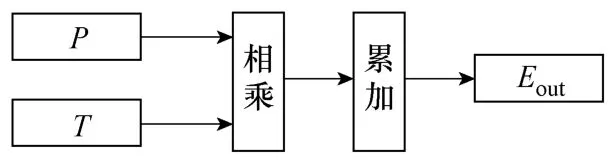
图2 电池能量观测单元原理图Fig.2 The schematic of battery energy observation unit

电池能量观测单元的输出值Eout达到设定值Eset时，表明来自外部电网的电能已经耗尽，以后电池放出的电能都来自油电转换。确定设定值Eset的具体方法将在第5节介绍。

4.3 改进等效燃油消耗最小的能量管理策略

PHEV动力电池充电有外部电网充电和发动机带动电机对电池充电两种途径。当电池SOC第一次降至soc1时，PHEV开始进入电量保持模式，电池中还有来自外电网的电能，此时消耗的电能来自上一次外部电网对电池充电，根据等效燃油消耗最小原理，此时不适用等效燃油消耗最小策略。

在电量保持模式阶段，发动机有时带动电机对电池充电，电池SOC值会上下波动，因此不能以SOC值作为判断来自外电网的电能是否已经消耗尽的标准。本文利用设计的电池能量观测单元的输出值来判断来自外电网的电能是否已经消耗尽。当电池能量观测单元输出值Eout大于设定值Eset时，说明电池中来自外电网的电能已经消耗尽，如果电池继续放电，消耗的电池电量来自油电转换，此时适用等效燃油消耗最小策略。综上所述，结合基于确定性规则的能量管理策略得到如表3所示的能量管理策略。

表3 能量管理策略Tab.3 The energy management strategy

5 仿真实验及结果分析

仿真所用的Plug-In并联式混合动力汽车模型的主要部件参数见表4。

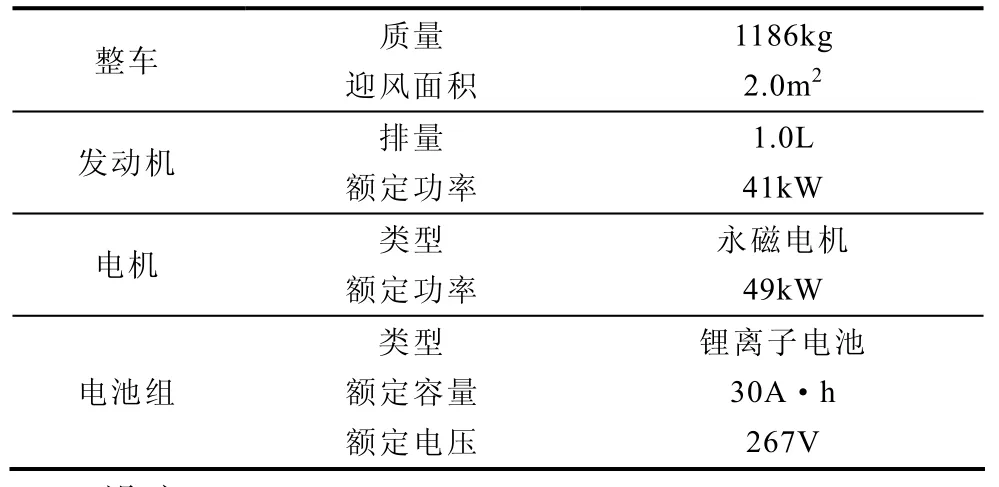
表4 模型的主要部件参数Tab.4 The main component parameters of model

设定soc1=0.5，soc_lo=0.4，soc_hi=0.6，SOC的初值soc_init为0.95。

电池能量观测单元设定值Eset的确定方法如下：

由电池SOC的定义可知

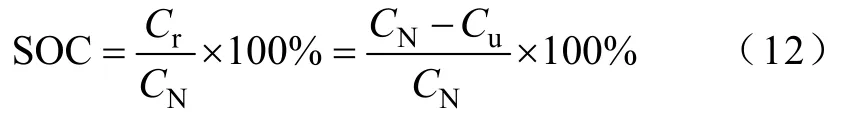
式中Cr—电池剩余容量；

Cu—已消耗电量；

CN—电池额定容量。

式中Ibat—t时刻的放电电流；

T—放电总时间。

为了简化计算，假设电池电压保持在额定电压。由下式计算电池总能量

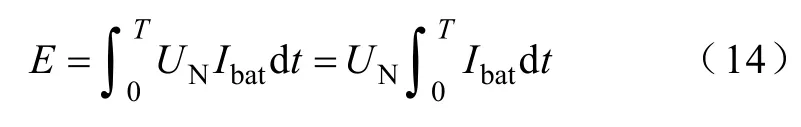
式中E—总能量；

UN—电池额定电压。

由式（11）～式（13）可以得到，SOC由soc_init降到soc_lo时电池放出的能量为Eset=E×

在ADVISOR平台上分别对基于确定性规则的能量管理策略（策略A）和本文提出的基于等效燃油消耗最小的实时优化能量管理策略（策略B）进行了测试。燃油经济性指标采用百公里耗油量表示，其数值越小，燃油经济性越好。在城郊循环路况WVUSUB的仿真结果见表5（一个WVUSUB循环路况的行程约为12km）。由表5可知针对不同的循环路况个数（不同行驶里程），策略B与策略A相比，燃油经济性都有显著的提高。

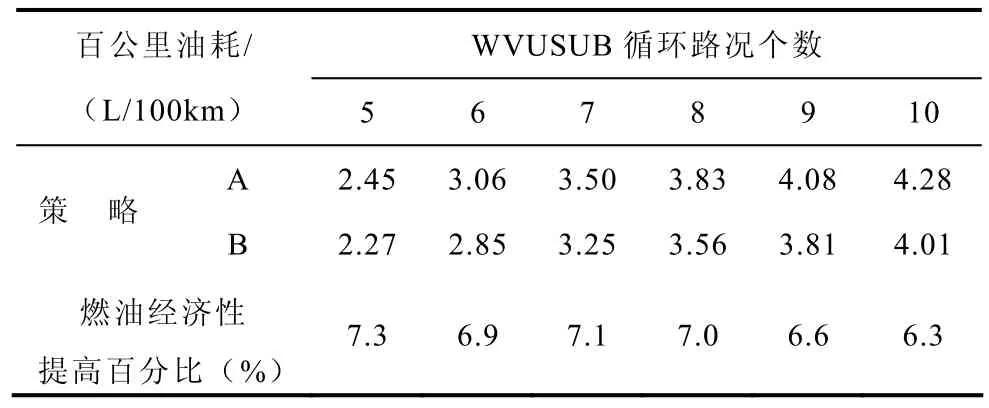
表5 WVUSUB循环路况上的仿真结果Tab.5 The simulation results of WVUSUB cycle

六个WVUSUB循环路况如图3所示，相应地策略A与策略B的SOC变化情况如图4所示，电机和发动机输出转矩Tm、Te分别如图5和图6所示。

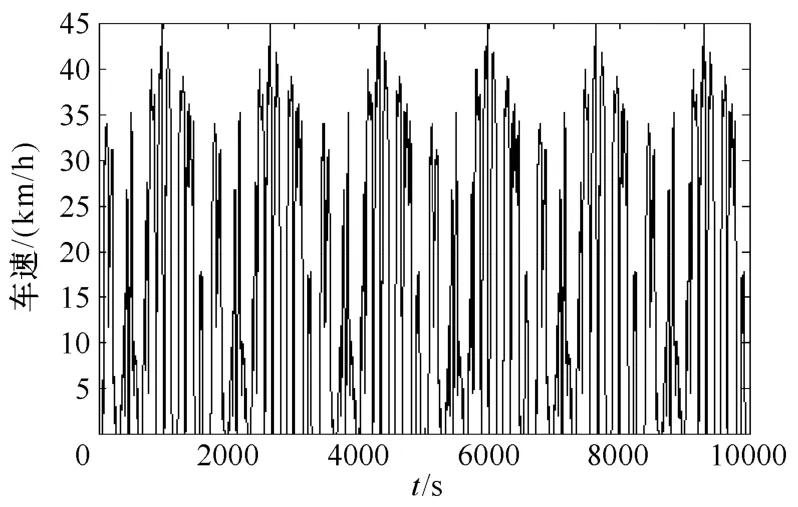
图3 六个WVUSUB循环路况Fig.3 6 WVUSUB drive cycles

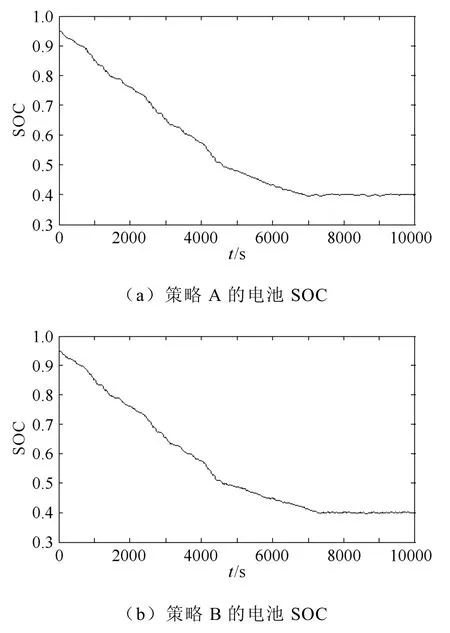
图4 策略A、B的电池SOCFig.4 Battery SOC of A strategy and B strategy

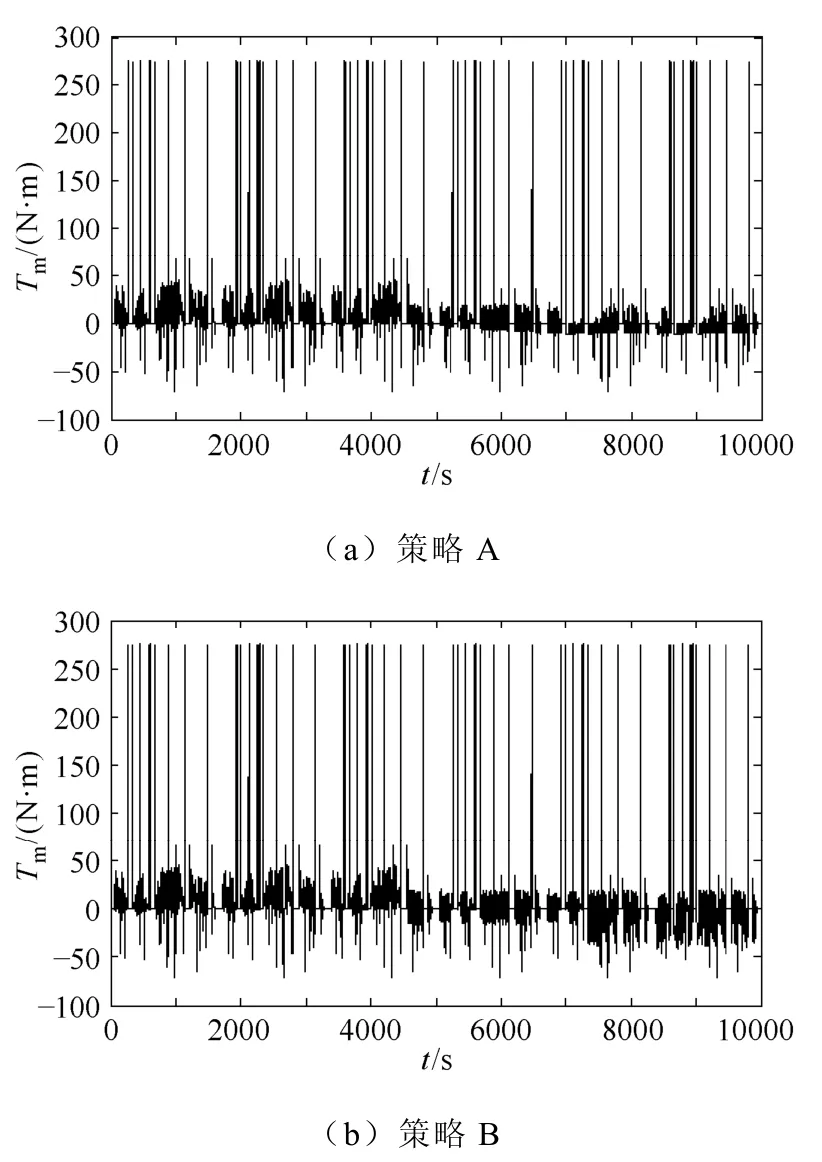
图5 应用策略A、B时的电机输出转矩Fig.5 The motor output torque for A,B strategy

本文还在MANHATTAN循环路况上进行了仿真实验。仿真结果见表6，一个MANHATTAN循环路况行程约为3.33 km，针对不同的循环路况个数，策略B与策略A相比，燃油经济性都有不同提高。

图6 应用策略A、B时的发动机输出转矩Fig.6 The engine output torque for A,B strategy

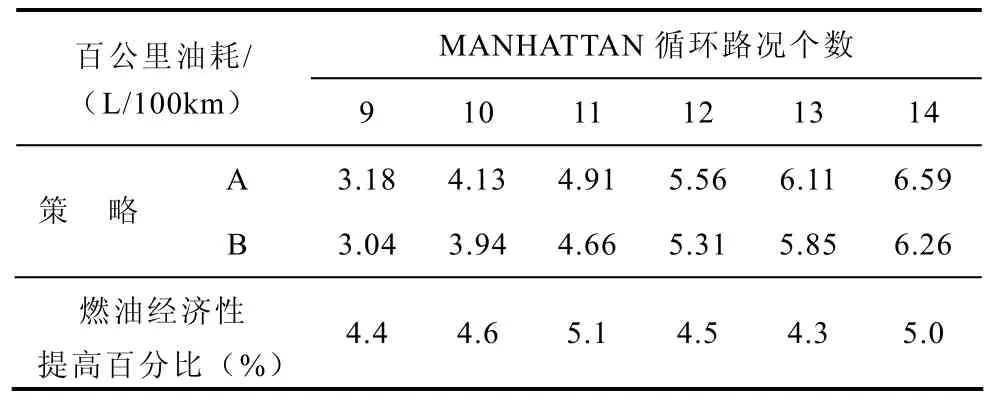
表6 MANHATTAN循环路况上的仿真结果Tab.6 The simulation results of MANHATTAN drive cycle

6 结论

本文结合PHEV的特点，设计了能量观测单元，并利用能量观测单元把等效燃油消耗最小策略应用于PHEV的能量管理中。在多种循环路况上的仿真结果表明，本文提出基于等效燃油消耗最小的实时优化能量管理策略能够在发动机和电机之间合理的分配转矩，有效地提高燃油经济性。

[1] Gong Qiuming,Li Yaoyu,Peng Zhongren.Trip based optimal power management of plug-in hybrid electric vehicle with advanced traffic modeling[J].SAE International Journal of Engines(S1946-3936),2009,1(1): 861-872.

[2] Salmasi F R.Control strategies for hybrid electric vehicles: evolution,classification,comparison,and future trends[J].IEEE Transactions on Vehicular Technology(S0018-9545),2007,56(5): 2393-2404.

[3] Banvait H,Anwar S,Chen Yaobin.A rule-based energy management strategy for plug-in hybrid electric vehicle (PHEV)[C].Proceedings of the American Control Conference,St.Louis,MO,USA,2009: 3938-3943.

[4] 张博,李君,高莹,Plug-in混合动力汽车能量管理策略优化设计[J].农业机械学报,2009,40(9): 20-25.Zhang Bo,Li Jun,Gao Ying.Optimization of plug-in hybrid electric vehicle energy management control strategy[J].Transactions of the Chinese Society for Agricultural Machinery,2009,40(9): 20-25.

[5] Wu Jian,Cui Naxin,Zhang Chenghui,et al.PSO algorithm-based optimization of plug-in hybrid electric vehicle energy management strategy[C].Proceedings of the 8th World Congress on Intelligent Control and Automation,2010: 3997-4002.

[6] Stephanie Stockar,Vincenzo Marano,Giorgio Rizzoni,et al.Optimal control for plug-in hybrid electric vehicle applications[C].Proceedings of the American Control Conference,Marriott Waterfront,Baltimore,MD,USA,2010: 5024-5030.

[7] Emadi A,Young Joo Lee,Rajashekara K.Power electronics and motor drives in electric,hybrid electric,and plug-in hybrid electric vehicles[J].IEEE Transactions on Industrial Electronics (S0278-0046),2008,55(6): 2237-2245.

[8] 陈清泉,孙逢春,祝嘉光.现代电动汽车技术[M].北京: 北京理工大学出版社,2002.

[9] 杨金星,周荣,乔维高.Plug-in 混合动力电动汽车的研究分析[J].汽车工程师,2009,(10): 23-25.Yang Jinxing,Zhou Rong,Qiao Weigao.Study on plug-in hybrid electric vehicle[J].Auto Engineer,2009,(10): 23-25.

[10] Gong Q M,Li Y Y,Peng Z R.Trip-based optimal power management of plug-in hybrid electric vehicles[J].IEEE Transactions on Vehicular Technology,2008,57(6): 3393-3401.