QC-LDPC码在OFDM-IDMA 系统中的性能研究
余格非,栗铁桩,张晓克
(重庆通信学院,重庆 400035)
0 引言
OFDM-IDMA(orthogonal frequency division multiplexing-interleave division multiple access)是近几年才被提出的新技术,它融入了以往多址接入技术的优点,表现出了巨大的研究潜力,因而受到国内外许多专家学者的关注。Mahafeno等[1]研究了准静态瑞利衰落信道环境下的OFDM-IDMA系统性能,同时将它和IDMA(interleave division multiple access)系统做了比较研究,证明了OFDM-IDMA具有更好的抗ISI(inter-symbol interference)性能。YangKai和Wang Xiandong[2]提出和分析了应用于超宽带无线通信环境中的OFDM-IDMA下行链路模型,并与相似系统结构的MC-CDMA系统进行了仿真比较研究。国内,也有许多学者对IDMA技术进行了大量的研究工作[3-5],但是对OFDM-IDMA系统的研究还非常少,目前只有清华大学的李云洲等人在系统频谱效率方面对OFDM-IDMA系统进行了探讨,并在最大比合并接收算法下,研究了系统的频谱效率与天线数的关系[6]。从国内外的研究现状来看,各国实验室对OFDM-IDMA系统的研究主要集中在系统结构和方案的设计、系统性能分析以及与传统多址方案(特别是OFDM-CDMA)的比较研究等方面,还没有深入到OFDM-IDMA系统的信道编码研究方面。本文对基于QC-LDPC(quasi cyclic low density parity check codes)编码的OFDM-IDMA系统展开研究,设计了一个三者融为一体的新方案并对其系统性能进行研究,其目的是寻求一个从多址接入技术、调制技术到纠错编码方案等方面,满足下一代无线移动通信高速率、高可靠性需求的整系统解决方案,同时为相关标准的确立提供理论依据和参考。
1 OFDM-IDMA系统结构
1.1 OFDM信号模型
OFDM系统信号模型框图如图1所示。在发射端,串行输入的二进制信号经过信道编码、符号映射后,通过串/并转换,成为并行信号,经过信号映射模块,输入到 IFFT(inverse fast-Fourier-transformation)模块,在生成的时域信号之前为了对抗符号间干扰[7],插入循环前缀(cyclic prefix,CP),此后信号分别经过并/串转换和D/A转换滤波后再发射到无线信道中。而在接收端,接收机对接收到无线传输的信号后执行与发送端相反的过程,对通过估计出的信道系数进行均衡处理后系统可以检测出发送的符号,然后进行符号解映射和信道译码,就可以恢复出发送的二进制序列。
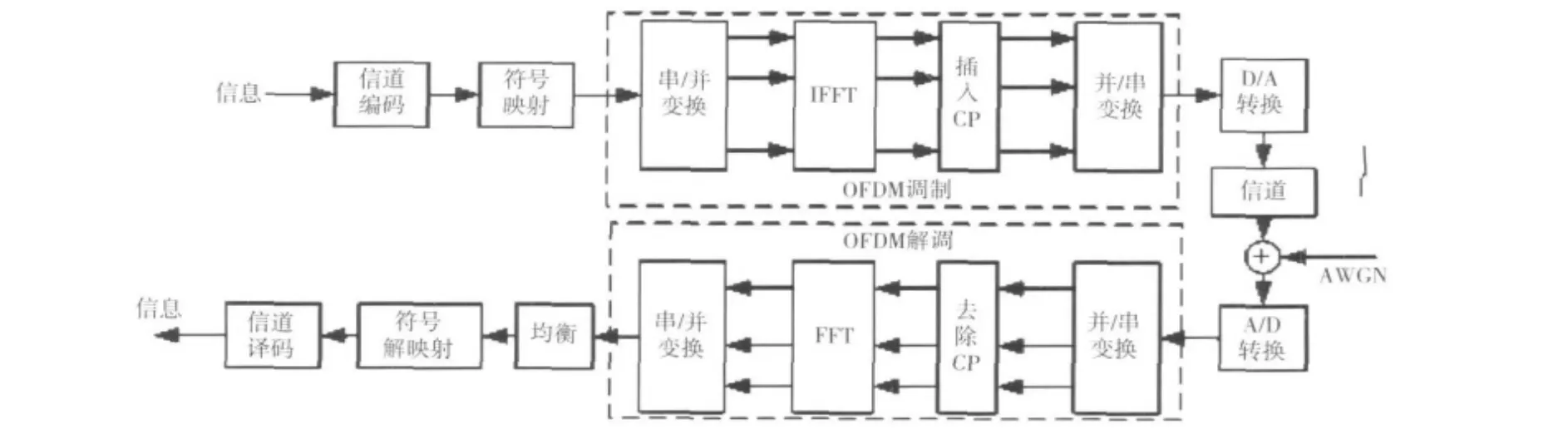
图1 OFDM系统信号模型Fig.1 Signalmodel of OFDM system
1.2 IDMA系统结构
IDMA系统的发送和接收结构原理如图2所示。IDMA系统采用交织器作为区分用户的唯一手段,不同的用户通常采用不同的交织序列,这样CDMA系统中扩频码所使用的全部带宽都可以释放出来用于信道编码[8]。可见,IDMA是CDMA的一种特殊形式,所以IDMA系统继承了CDMA系统抗干扰性及抗多径衰落等优点。但IDMA因为其自身的结构组成原理,所以还具有许多优势,即采用一个简单的码片到码片的迭代多用户检测的接收结构,就可以使其具有更高的频谱利用效率、更优良的多用户通信性能及较低的接收机复杂度等。
如图2所示,IDMA系统的发送端考虑了K个仿真用户,假设 dk= [dk(1),…,dk(i),…,dk(I)]T(I为信息码元的长度)为第k个用户的输入信息码元序列,经过前项纠错码编码器CFEC产生编码序列为 bk= [bk(1),…,bk(l),…,bk(L)](L 为编码长度),再经过重复码编码器CREP进行扩频操作,每个码元bk(l)被重复S次编码成低码率码序列ck=[ck(1),…,ck(j),…,ck(J)]T(J=L × S,为低码率码编码长度,也是发送码片序列的长度),编码器CFEC和CREP就构成了一个低码率码编码器C,最后经过交织器{πk}重新生成发送序列xk=[xk(1),…,xk(j),…,xk(J)]T,在 CDMA 系统中,通常称发送序列xk(j)中的码元为“片”(Chips)。
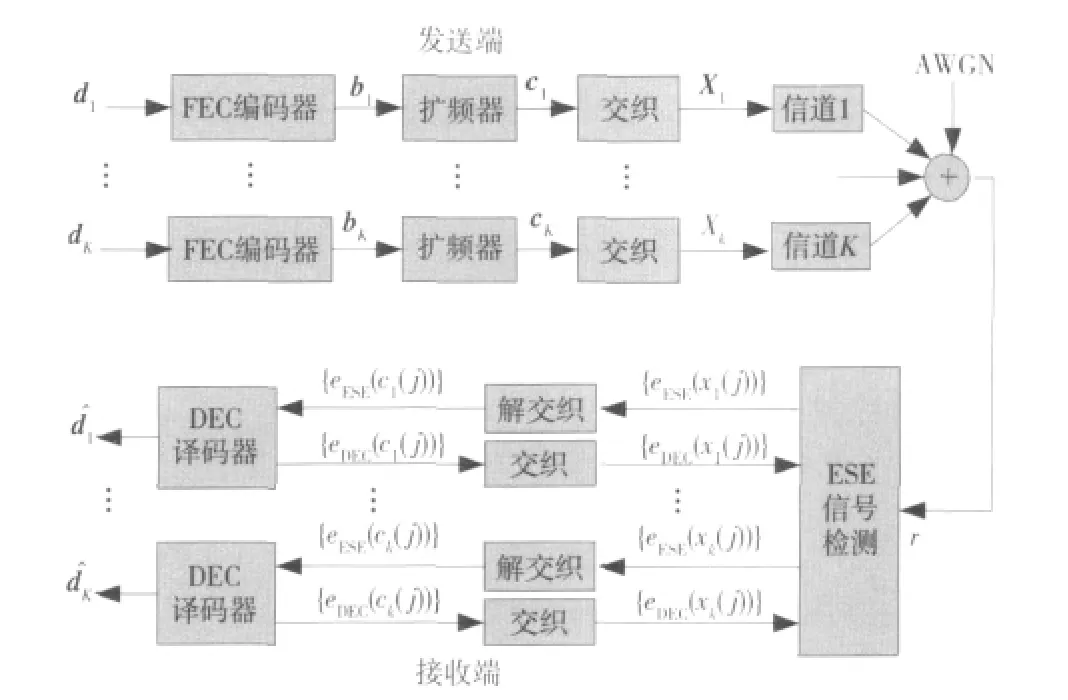
图2 IDMA系统的发送和迭代接收结构Fig.2 Transmittion and iterative scheme of IDMA system
IDMA技术中一个最重要的原则就是对不同用户的交织器{πk}采用不同的映射规则,交织器映射规则的产生必须是随机和独立的。交织器的使用打乱了编码序列的顺序,使相邻的码片近似无关,从而使片到片的多用户检测变得较为容易。
IDMA系统在接收端采用一个次优的turbo型迭代译码结构,包括了一个基本信号检测器(elementary signal equipment,ESE)和K个单用户的后验概率(a posteriori probability,APP)译码器(DECs)。多址接入和编码限制的问题可以分解为ESE和DECs单独处理。ESE和DECs模块的输出值是通常所说的外信息,定义为

(1)式中,用下标来区分分别由ESE和DECs模块产生的外信息,表示为eESE(xk(j))和eDEC(xk(j))。并且由ESE和DECs模块产生的外信息来完成一个全局的片到片的Turbo型迭代接收过程,经过M次迭代以后,K个用户的DECs分别产生相应的信息序列dk的硬判决值。
1.3 OFDM-IDMA系统模型
仿真用户数为K的OFDM-IDMA系统上行链路发送及接收结构如图3所示,在发送端,假设第k个用户产生的数据流为dk,通过前向纠错编码和重复编码后,产生片序列ck={ck(j)}。然后,在每个用户特定的交织器作用下,并经过符号映射后,得到符号序列xk=[xk(1),…,xk(j),…,xk(J)]T(其中 J为帧长),然后,通过IFFT将这些符号调制到不同子载波上。
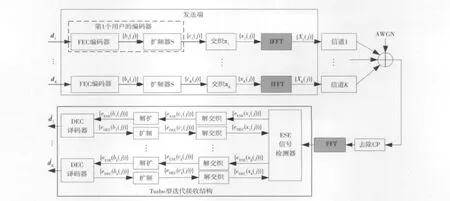
图3 OFDM-IDMA系统的发送接收框图Fig.3 Transmitter and receiver structure of IDMA system
在接收端,OFDM解调在迭代多用户检测之前完成。这里假设CP的持续时间大于多径信道的最大时延,则在去掉循环前缀和OFDM解调之后的得到的接收信号可以为

(2)式中:Z(j)是方差为σ2的复高斯白噪声z(j)的FFT变换,即Z(j)=FFT(z(j));Hk(j)为第j个子载波的衰落系数,其表达式为

单径复信道的CBC检测算法在文献[4]中进行了详细描述。对于OFDM-IDMA系统,在频率选择性信道中,OFDM子载波上的衰落系数{Hk(j)}对不同的j是不一样的。
2 QC-LDPC码型构造
准循环LDPC(QC-LDPC)码是一类特殊的LDPC码。准循环LDPC码是由其奇偶校验矩阵来定义的。它的奇偶校验矩阵是由一些零阵和循环置换阵构成[9-12]。令P是一个b×b的置换阵:

Pi为单位阵I循环移动i次而得到的循环置换阵,其中0≤i≤b。同时,P意味着零矩阵。令H为cb×tb的矩阵定义为

LDPC码的构造在本质上等价于构造一个稀疏的校验矩阵H。LDPC码可以通过图论法、有限几何法、组合设计法和代数法等方法来构造。本论文中的LDPC码采用了基于有限几何的构造法生成,此种方法构造出的LDPC码的生成矩阵和校验矩阵可以具有循环或者准循环的结构。下面简要介绍基于准循环结构的LDPC码的构造算法。
准循环LDPC码由于其结构的特殊性,只要有一个小环,就至少存在b个同样大小的环,小环的存在对码的性能影响很大,因此构造时要考虑避免小环的存在。准循环LDPC码环的分布只与ai,j的取值有关(ai,j为各个循环子矩阵循环右移的位数)。因此对准循环LDPC码的环的分析比较简单。
各个小矩阵循环右移的位数可写成一个矩阵

在该矩阵上按行列交替顺序可以画一个环路,若奇数节点上的数值和与偶数节点上的数值和相同(模b),则该环路构成一个环,否则不构成环[11]。一般情况下,相同码长和码率的消去4环后随机构造的准循环LDPC码的性能基本相同,并且消去4环最简单,这样只需保证(6)式中任意一个矩形的2个对角线元素和相等(模b)。准循环LDPC码就可以通过消4环后随机构造再择优选取而得到[11],具体构造算法如下:
步骤1将所有子矩阵循环右移的位数初始化为0。
步骤2从第2行第2列开始按先列后行的顺序,在1到b-1之间随机产生数,每个新产生的随机数与已经产生的所有随机数进行比较,如有相同就重新产生一个该位置的随机数并重新进行比较,直到重新产生的随机数与己经产生的所有随机数都不同为止。
步骤3从第2行开始与后面各行开始逐行检查两行所构成的所有矩形的2个对角线元素的模b和是否相等,无需检查第1列,若发现有相等的,返回步骤2。
步骤2保证了包含第1行和第1列元素所有矩形的对角线元素模b和不会相等,步骤3保证了其他矩形的对角线元素模b和不会相等,因此该算法生成的准循环LDPC码不会存在4环的可能。当然随机数产生的同时,也可以考虑其他矩形的对角线元素模b和是否相等,但程序的编写比较复杂,而且当b值比较大,而r和c值比较小时,上述算法的重复次数还是相当少的。这样就可以产生准循环LDPC码的校验矩阵各个子矩阵循环右移的位数。
3 基于QC-LDPC编码的OFDM-IDMA系统结构
基于QC-LDPC码编码的OFDM-IDMA系统结构框图如图4所示。
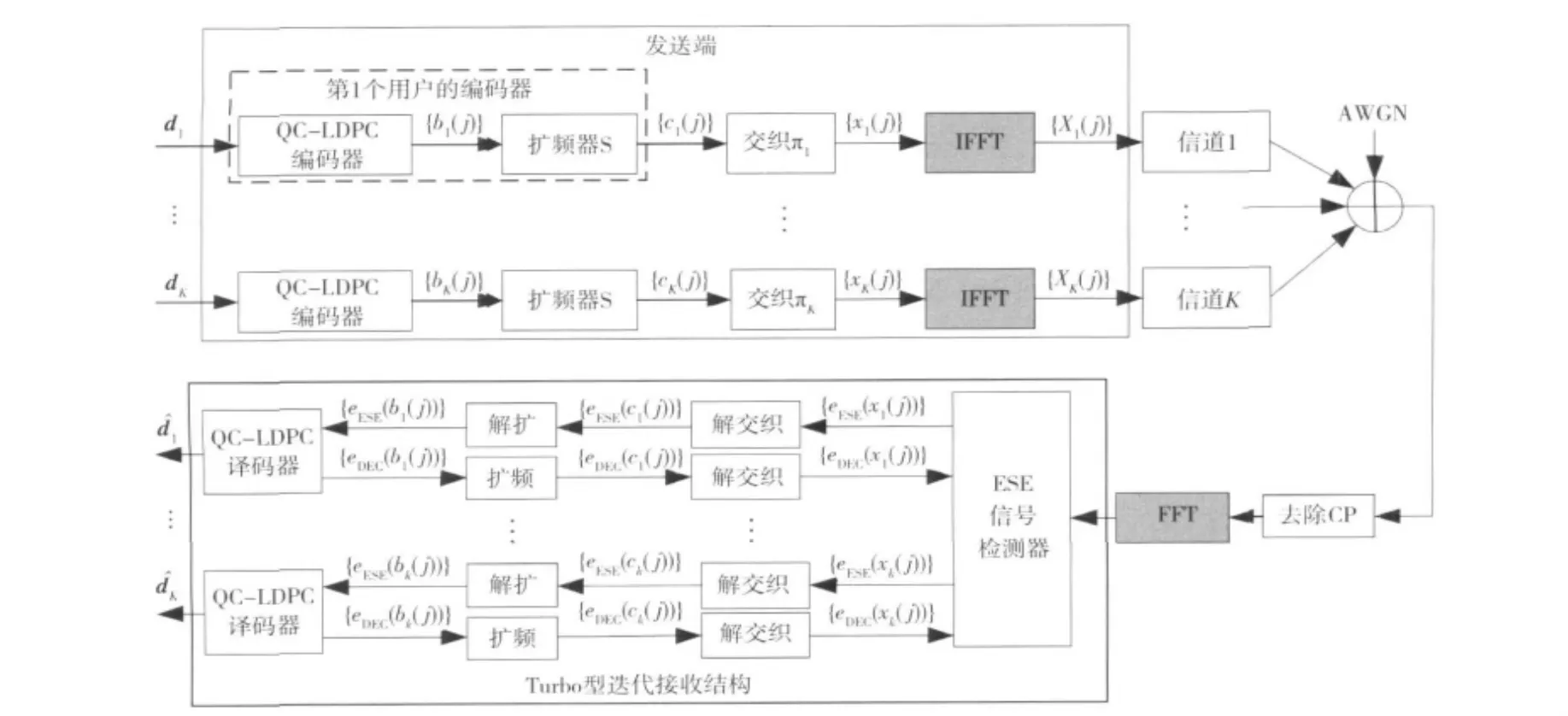
图4 基于QC-LDPC编码的OFDM-IDMA系统结构Fig.4 OFDM-IDMA system model with QC-LDPC
假设发送端有K个用户接入,以第一个用户为例,首先产生离散的二进制数字信号序列d1,然后经过QC-LDPC编码器编码产生编码序列b1,经过扩频器后产生低码率序列c1,接下来经过随机交织器打乱原来的序列,再经过符号映射(BPSK或QPSK)后,产生发送序列 xk=[xk(1),…,xk(j),…,xk(J)]T,最后,通过IFFT将这些符号调制到不同子载波上。
在接收端,K个用户的发送信号序列经过AWGN信道后进入接收端以前,首先需要去除循环前缀,然后再进行FFT变换,产生r序列:
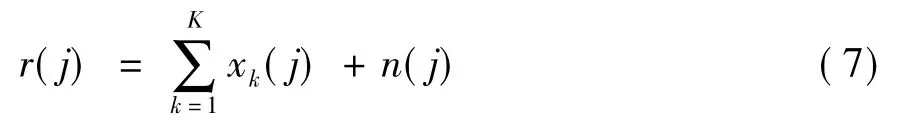
(7)式中,n(j)为满足均值为0,方差为1的高斯白噪声。
上述接收信号送入ESE模块进行处理后分别产生K个用户的接收序列,接收序列的值是对发送序列的概率估计,即前面所说的外信息。以第1个用户为例,经过 ESE模块后产生的外信息{eESE(x1(j))}经过解交织器恢复原顺序,产生的解交织序列{eESE(c1(j))}送入译码器进行译码,译码器译码后产生外信息{eDEC(c1(j))}经过交织器交织后才返还给ESE模块,完成一次迭代接收的过程。经过n次迭代以后,译码器才能产生发送端二进制离散数字序列的硬判决值。
需要说明的是:每个用户接收端和发送端必须具有相同的交织器,解交织器与交织器必须相对应;译码器除包含解扩、QC-LDPC译码和扩频操作,还分别与发送端的扩频器和QC-LDPC编码器相对应。
4 QC-LDPC编码的OFDM-IDMA系统仿真与研究
4.1 仿真参数
本文仿真了AWGN信道下,不同码率和帧长的QC-LDPC在OFDM-IDMA系统下的性能,并与基于卷积码编码的OFDM-IDMA系统的性能进行了比较。
码率Rc分别采用0.5,0.75和0.875的QC-LDPC(1 200,600),QC-LDPC(4 088,3 068)和 QC-LDPC(8 176,7 156),系统最大迭代次数为5次,译码均采用BP译码算法且迭代次数为20次。仿真了单用户和8个用户的情况,每个用户的扩频序列长度为8,子载波数为32个,调制方式采用BPSK调制。
帧长分别采用 1 020 bit,2 044 bit,4 088 bit,8 176 bit。译码均采用BP译码算法且迭代次数为50次,译码均采用BP译码算法且迭代次数为50次。分别仿真了单用户和8个用户的情况,每个用户的扩频序列长度为8,子载波数为32个,循环前缀长度为8,调制方式采用BPSK调制。
在与基于卷积码的OFDM-IDMA系统性能进行比较时,系统仿真中最大迭代次数为5次,QC-LDPC码采用QC-LDPC(2 044,1 020),译码算法为BP译码且迭代次数为50次;卷积码采用(31,27)系统递归型卷积码,译码采用软进软出的Map译码算法。2种编码系统的仿真用户数分别为1个和5个,编码码率 Rc均为0.5,扩频序列长度为8,帧长为2 044 bit。
4.2 仿真结果与分析
图5给出了不同码率的QC-LDPC编码的OFDM-IDMA系统性能仿真图,图6给出了QC-LDPC编码的OFDM-IDMA系统在不同帧长条件下单用户的性能仿真曲线图。从图5可以看出,无论是单用户还是多用户,随着码率的增加,系统误码率明显下降,性能显著提高,但要达到高质量通信要求则需要在发送端加大发送功率。从图6中可以看出,单用户条件下,各曲线的下降趋势均比较明显,表现出了良好的编码性能。短帧和中长帧条件下的系统具有更佳的性能,而帧长为8 176 bit的长帧情况下,系统表现出的性能要稍差于其他情况。图7说明了多用户情况下,短帧和中长帧的系统性能比较接近,但是帧长为4 088 bit的长帧情况下的系统性能要比其他情况要差,同时所有帧长下的性能均比单用户时有所恶化。

图5 不同码率的QC-LDPC编码的OFDM-IDMA系统性能仿真图Fig.5 Performance comparison of OFDM-IDMA with QC-LDPCswith different rates

图8为在AWGN信道下,我们所设计的基于QC-LDPC编码的系统与基于卷积码编码的系统性能对比仿真曲线图,如图8所示,5个用户的情况下,基于QC-LDPC编码的OFDM-IDMA系统在信噪比Eb/N0=4.2 dB以后,性能就明显优于相同用户数的基于卷积码的系统,而且曲线下降迅速。在误比特率达到10-6时,单用户情况下的基于QC-LDPC编码的系统比基于卷积码编码的系统可以多获得约2.8 dB的编码增益,5个用户时也可以多获得约1.6 dB的编码增益。可见,所设计的基于QC-LDPC编码的OFDM-IDMA系统的性能远优于采用卷积码的系统,因此更能适应未来高可靠性数据传输的需求。
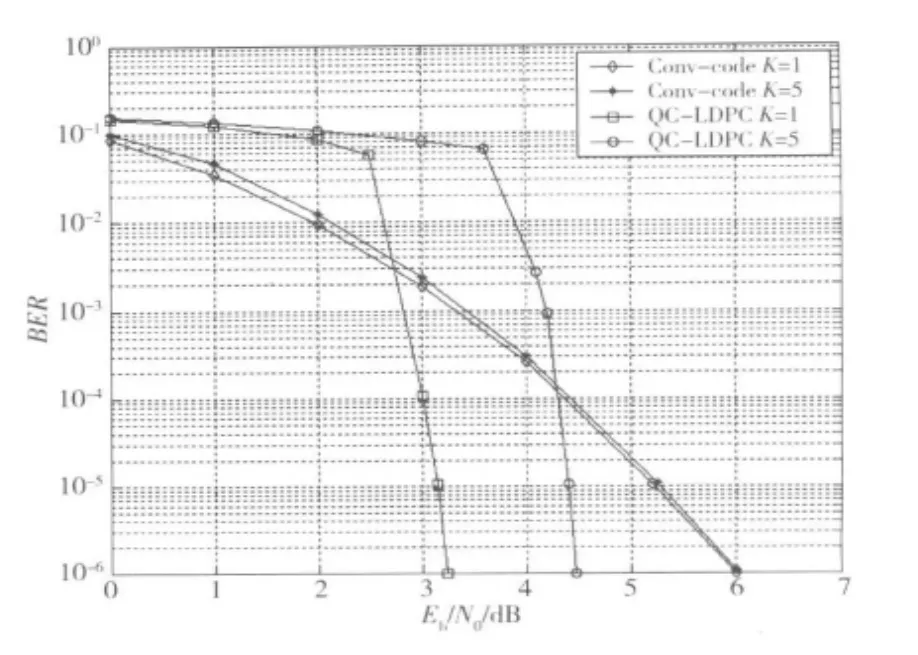
图8 基于QC-LDPC编码的系统与基于卷积码编码的系统性能比较仿真图Fig.8 Performance comparison of OFDM-IDMA with QC-LDPC and with convolutional codes
5 结论
本文设计了一种新的基于QC-LDPC码的OFDM-IDMA系统,并研究了该系统在不同码率、不同传输帧长条件下的性能,仿真结果表明随着码率的增加,系统的误码率曲线急剧下降,性能明显改善,而对于不同帧长的情况,短帧和中长帧情况比长帧表现出更好的纠错性能。通过与基于卷积码的OFDM-IDMA系统的性能比较,结果表明了本文所设计的系统比卷积码编码的OFDM-IDMA系统能够获得更大的编码增益,更加接近多址接入的信道容量限,因此更能适应未来高可靠性数据传输的需求。
[1] MAHAFENO I,LANGLAISC,JEGO C.OFDM-IDMA versus IDMA with ISIC for quasi-static Rayleigh fading multipath channels[C]//Proc.4th International Symposium on Turbo Codes & Related Topics,Munich,Germany: [s.n.],2006.
[2] YANG Kai,WANG Xian-dong.A Multicarrier Chip-interleaved Multiuser UWB System [C]//Acoustics,Speech,and Signal Processing,2005.Proceedings.(ICASSP'05).IEEE International Conference,[s.l.]:IEEE Press,2005(3):iii/325-iii/328.
[3]LIPing,LIU L H,WU K Y,et al.Interleave division multiple access(IDMA)communication systems[C]//Proc.3rd International Symposium on Turbo Codes& Related Topics,[s.l.]:IEEE Press,2003:2157-2161.
[4]LIPing.Interleave-division multiple access and chip-bychip iterative multi-user detection[J].Communications Magazine,IEEE,2005,43(6):S19-S23.
[5]LIPing,LIU L,WU K Y,etal.Interleave-divisionmultiple-access[EB/OL].[2011-01-09](2006-12-17)http://www.ee.cityu.edu.hk/~ liping/Research/Journal/idma2.pdf.
[6]ZHOU S,LI Y,ZHAO M,et al.Novel techniques to improve downlink multiple access capacity for B3G[J].IEEE Commun Mag,2005,43:61-69.
[7]李向宁,谈振辉.OFDM基本原理及其在移动通信中的应用[J].重庆邮电大学学报:自然科学版,2003,15(2):25-30.
LIXiang-ning;TAN Zhen-hui,OFDM Principle and Its Applications in Mobile Communication[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2003,15(2):25-30.
[8] 罗尧,王琳,凌珺.基于LDPC编码的交织多址接入(IDMA)系统[J].重庆邮电大学学报:自然科学版,2006,18(5):581-584.
LUO yao,WANG Ling,LING jun,Interleave Division Multiple Access System Using LDPCCodes[J].Journalof Chongqing University of Posts and Telecommunications:Natural Science Edition,2006,18(5):581-584.
[9]FOSSORIER Marc PC.Quasi-cyclic Low-density Paritycheck Codes form Circulant Permutation Matrices[J].IEEE Transactions on Information Theory,2004,50(8):1788-1793
[10]SEHOM,KYEONGCHEOL Y,JAEYOEL K.Quasi-cyclic LDPC Codes for Fast Encoding[J].IEEE Transactions on Information Theory,2005,51(8):2894-2901.
[11] FOSSORIER M.Quasi-cyclic Low Density Parity Check Codes[C]//Proc.2003 IEEE Int Symp Information Theory.Yokohama,Japan:[s.n.],2003:150.
[12] SRIDHARAN A,COSTELLO Jr D J,SRIDHARA D,et al.A Construction for Low-density Parity Check Convolution Codes based on Quasi-cyclic Block codes[C]//Proc.IEEE Int Symp Information Theory(ISIT2002).Lausanne,Switzerland:IEEE Press,2002:481-485.

