局部应变法预测飞机结构带孔部件疲劳寿命

童第华, 陈志伟

(1.北京航空材料研究院,北京 100095;2.北京航空工程研究中心,北京 100076）

局部应变法预测飞机结构带孔部件疲劳寿命

童第华1, 陈志伟2

(1.北京航空材料研究院,北京 100095;2.北京航空工程研究中心,北京 100076）

介绍了应用Levenberg-Marquardt迭代法计算局部应力和局部应变的工作。Levenberg-Marquardt迭代法是求解超越方程的一种常用数学方法,但是缺点是程序比较复杂,计算效率较低,因此本文目的是找到一种程序实现简单、计算效率高、计算精度满足要求的计算方法,选择了二分法,并且对比分析了二分法和Levenberg-Marquardt迭代法求解局部应变与应变寿命方程的效率和精度,从而得出应用二分法来进行求解是简单并且可以被工程应用的;最后结合某飞机结构一种带孔部件的实例,应用局部应力应变法给出了该部位的寿命预测值,通过和试验寿命值的对比,得出了考虑平均应力修正的应变寿命方程才更符合工程要求。

局部应力应变法;Levenberg-Marquardt迭代法;二分法;应变寿命方程;平均应力修正

金属在较高的循环应变作用下发生的疲劳失效,称为应变疲劳。金属材料的应变疲劳寿命一般都较短,故将应变疲劳称为低周疲劳,即短寿命疲劳。局部应力应变法结合材料的循环应力应变曲线,通过弹塑性有限元分析或其他计算方法,将构件上的名义应力谱转换为危险部位的局部应变(应力）谱,然后根据危险部位的局部应力应变历程估算寿命[1]。

结构在其服役期间总体上处于弹性范围内,但某些疲劳危险部位在大载荷情况下却进入弹塑性状态,应力和应变关系不再是线性关系,塑性应变成为影响其疲劳寿命的主要因素。局部应力应变法在疲劳寿命估算中考虑了塑性应变的影响和载荷顺序的影响,因而用它估算结构的疲劳裂纹形成寿命通常可以获得比较符合实际的结果[2]。

本研究就局部应力应变法展开研究,应用Levenberg-Marquardt迭代法和二分法来求解局部应力、局部应变和应变寿命公式,并对两种方法的计算结果进行比较分析;进一步分析了应变寿命公式平均应力修正的必要性;结合某飞机结构一种带孔部件的模拟试件,给出预测的疲劳寿命,并与试验寿命进行比对分析。

1 局部应力应变法估算结构疲劳寿命的步骤[3]

用局部应力应变法估算结构疲劳寿命,首先估算疲劳危险点的弹塑性应力应变历程,然后对照材料的疲劳性能数据,按照疲劳累积损伤理论,进行循环续循环的疲劳损伤的累积,最后得到构件的疲劳寿命,其步骤如图1。

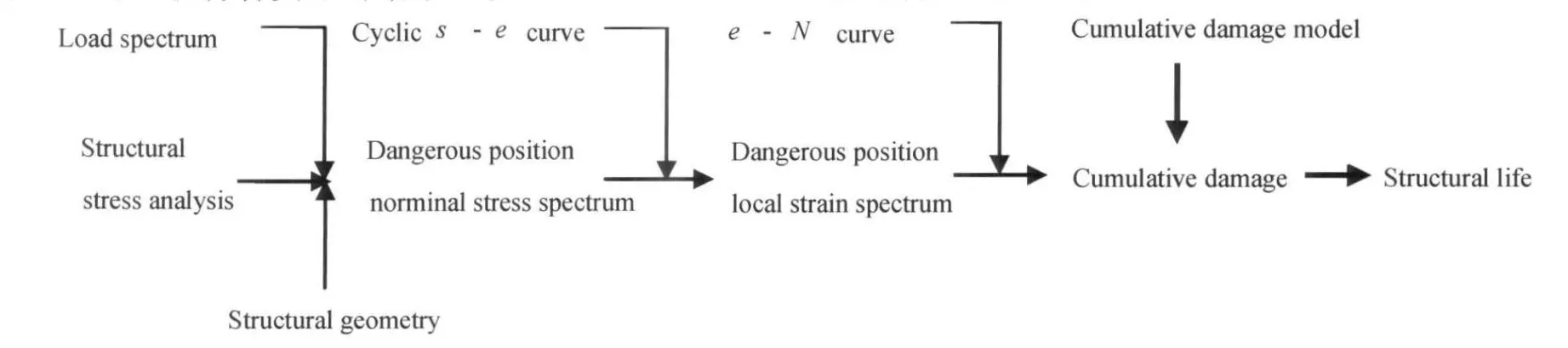
图1 局部应力应变法寿命估算的步骤Fig.1 Process of local stress-strain method

2 局部应变和局部应力的求解

本研究主要采用Neuber法来计算缺口根部的局部应力和局部应变[4]。Neuber提出的计算缺口根部弹塑性应力应变的方程为:

式中KT为理论应力集中系数;Kσ=σ/S为应力集中系数,σ为缺口根部的局部应力,S为名义应力,在试验件处于弹性时,Kσ=KT;Kε=ε/e为应变集中系数,ε为缺口根部的局部应变,e为名义应变,在试验件处于弹性时:

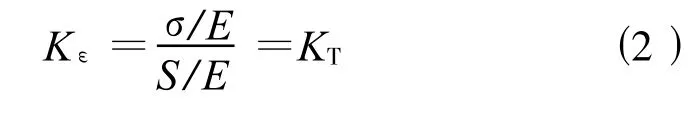
在工程实际中,通常结构整体上处于弹性,即名义应力S和名义应变e之间为弹性关系S=Ee,将此带入式(1）得:

式中C被称之为Neuber常数;E为弹性模量。

Morrow[5]等认为,在循环加载条件下,切口根部的局部应力范围 Δσ和局部应变范围 Δε,也可以用式(3）计算,于是:

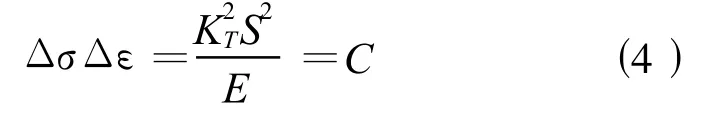
材料的稳态循环应力-应变曲线,可用下式表示:

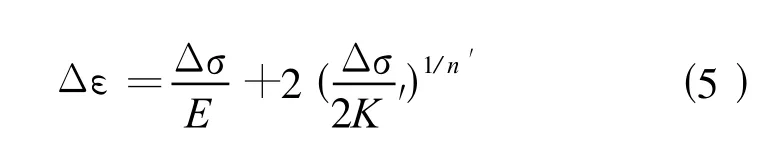
式中K′为循环强度系数,n′为循环应变硬化系数。

将式(4）和式(5）联立求解,从名义应力即可得到局部应力和应变(Δσ和 Δε）之值,这样问题就转化为对(4）和(5）这个超越方程组精确求解的问题,本文后面会对这个问题进行详细的阐述。

3 应变寿命的求解

在所有的应变寿命公式中,Manson-Coffin公式[6]使用最为广泛,其表达式为:

由于大多数给出的Manson-Coffin公式的参数是在Rε=-1下得到的,而实际疲劳载荷几乎都是非对称应变循环,因此在使用Rε=-1下的 Δε-N曲线进行疲劳寿命估算时,需要对 Δε-N曲线进行修正。一些学者在这方面做了很多工作,提出了一些很有价值的考虑平均应力修正的应变寿命公式[7],如Morrow平均应力修正公式:

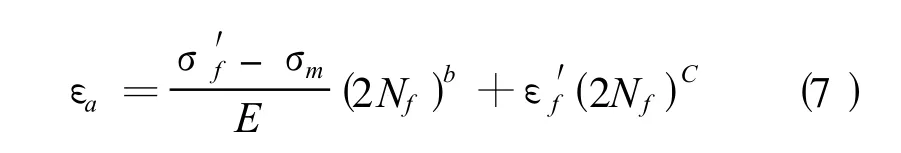
本研究就根据Morrow方法对Rε=-1的 Δε-N曲线进行修正。

通过上节的分析我们可以得到每个循环的局部应力和局部应变值,将局部应变值带入式(7）即可求出当前应变幅值下的寿命Nf,那么现在的问题就是精确求解这个超越方程。求解超越方程(4）,(5）和(7）的方法也有很多,被广泛应用的是二分法(区间对分）和迭代法,下面就对这两种数值算法进行对比分析。

4 超越方程的数值解法

4.1 Levenberg-Marquardt法

在求解 Δσ和 Δε以及应变寿命方程的过程中,一方面需要求解超越方程,另外由于载荷谱是一个较长较复杂的载荷历程,所以必须借助计算机对很长的峰谷历程逐个循环求解。

对下列一般非线性方程组(8）:

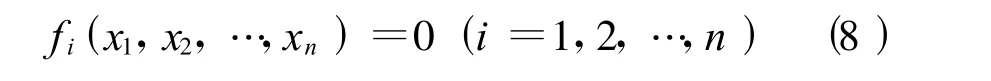
求解的方法有很多,最常用的是采用迭代方法逐步逼近近似求解。迭代求解该问题的方法,一般可利用成熟的软件包求解。本文就利用了MATLAB软件包中Levenberg-Marquardt法[8]求解局部应力和局部应变。

Levenberg-Marquardt方法是一种牛顿类型的方法。在普通的梯度算法中,收敛的方向始终是待解方程函数的梯度方向。而在Levenberg-Marquardt算法中,采用了一个方向矢量不断调整计算的收敛方向,可以获得更好的收敛性。其求解的主要过程为:设是的Jacobian矩阵,即式(9）,方程未知量的迭代法则可以用式(9）表示。

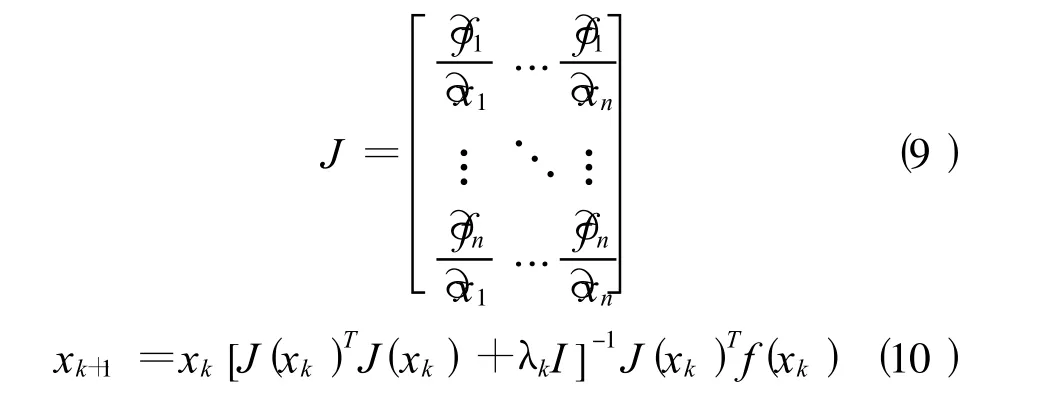
式(10）中为程序自动调整的试探性参数,为单位矩阵。

整个计算过程在MATLAB中进行,算法的每次迭代都对进行自适应调整,当接近一个解时,逐渐减小,迭代式(10）演变成Gauss-Newton法;当远离解时,λ逐渐增大,迭代式(10）则演变成梯度下降法,可以进行全局搜索,所以Levenberg-Marquardt算法同时具备了牛顿法的局部收敛性和梯度法的全局搜索性的优点。由于Levenberg-Marquardt算法中 [J(xk）TJ(xk）+λkI]是正定的,所以式(10）的解总存在,保证了算法的稳定性,算法流程图如图2。实际计算中,迭代增量s小于容许误差限(e=1.00E-10）即认为收敛,输出计算终值。

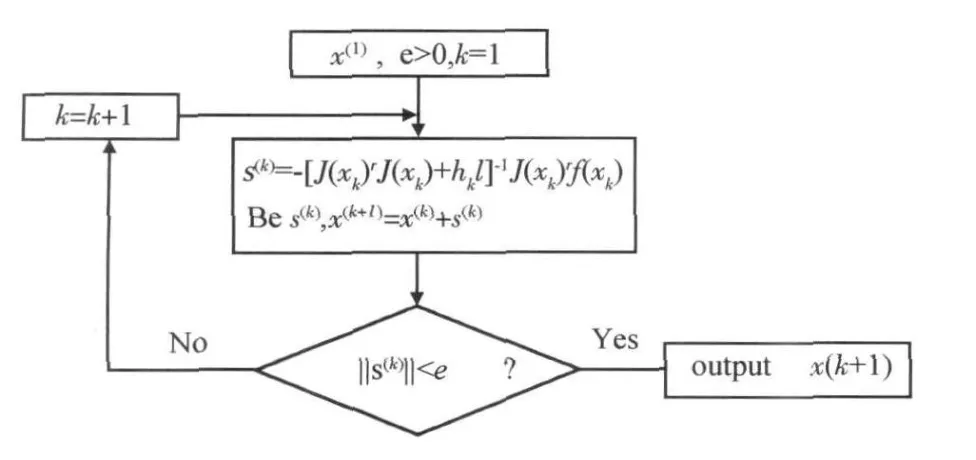
图2 Levenberg-Marquardt算法流程图Fig.2 Levenberg-Marquardt algorithm process chart

与其它迭代算法一样,Levenberg-Marquardt算法的计算结果依赖于初值的选取,合理的选取初值是保证计算结果快速收敛到所需精度的关键,本文用下面的方法巧妙的解决了这个问题。

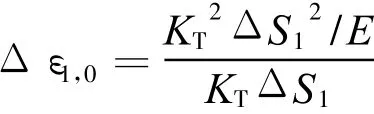
4.2 二分法

在应用Levenberg-Marquardt法求解上述超越方程的时候,我们发现Levenberg-Marquardt法的求解精度很高,但不足的是程序实现比较复杂,并且随着求解方程数量的增加计算效率显著下降,为此下面介绍下一种程序实现简单、计算效率高的计算方法—二分法。

应用二分法来计算时,首先需要定义一个含根的区间[a,b]。不失一般性,取为a=1,b=109。还需要明确f(Nf）的表达式:

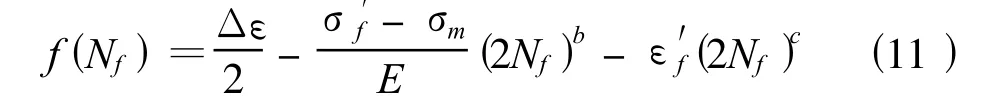
式中的 σ′f,E,b,c,ε′f均为材料参数。图 3给出求解上面复杂超越方程的二分法计算流程图。

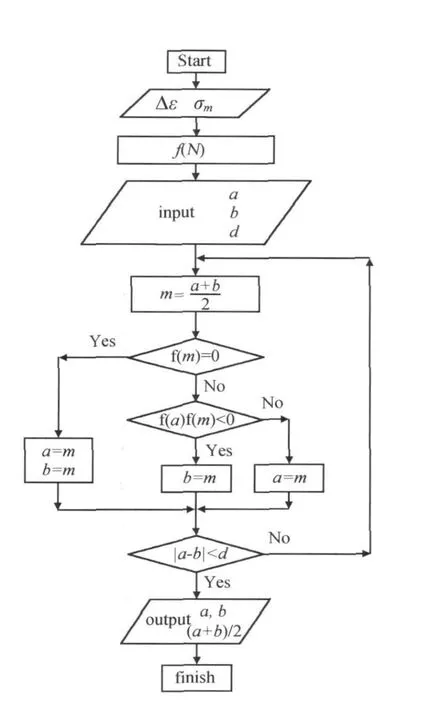
图3 二分法计算流程图Fig.3 Dichotomy calculation process chart

5 实验与计算结果

某型飞机一个带孔部件的模拟试件的具体材料数据如下:板宽W=12mm,孔直径 D=3.5mm。材料的性能常数为:弹性模量E=69000MPa,拉伸强度 σb=505MPa,循环强度系数K′=723.4MPa,应力集中系数Kt=2,循环硬化系数 n′=0.0845。应变疲劳参数为 σ′f=859.56MPa,b=-0.1023,c=-0.615, ε′f=0.88。表1给出了某型飞机一个带孔部件的模拟试件在某基准谱下试验结果。

我们根据式(4）和式(5）利用二分法和Levenberg-Marquardt迭代法求出的 Δε,将其带入到式(11）中就可求出当前应变幅下的寿命Nf。

例如,对于第一个循环,根据表2中求出的Δε,将其带入Manson-coffin公式,分别根据二分法和Levenberg-Marquardt迭代法来计算寿命Nf,其结果比较见表3。

表1 一个带孔部件模拟试件在某基准谱下试验结果Table 1 The test results of a hole part simulation specimen at X reference spectrum

表2 应用二分法和迭代法的Δε计算结果Table 2 The Δε calculate results of application dichotomy and iterative

表3 应用二分法和迭代法的寿命计算结果Table 3 The life calculate results of application dichotomy and iterative

从表2和表3中可以看出应用二分法和Levenberg-Marquardt迭代法计算出的局部应变结果和寿命结果都十分接近,也说明了计算结果是十分接近真值的,是可以被工程应用的,但是Levenberg-Marquardt迭代法的计算效率明显不如二分法,同时二分法程序编写简单,精度也满足要求,易于被工程上所应用,在此后计算寿命时,采用的就是二分法。

下表4是针对一个带孔部件在考虑了平均应力影响和未考虑平均应力影响应用二分法计算的寿命结果。

表4 平均应力修正对寿命预测值的影响Table 4 The average stress amend impact on the prediction life

从表4中我们可以看出,未考虑平均应力修正的计算模型,计算出的疲劳寿命值,远远高于试验寿命,而考虑了平均应力修正的计算模型,计算出的疲劳寿命和试验得到的疲劳寿命相近。这是因为此处实际随机谱的每个循环的平均应力虽不同但几乎都是正的,全部为正的平均应力对实际的计算结果产生很大的影响;而未考虑平均应力修正的计算模型,相当于把平均应力都当0来处理,这明显不符合实际情况,所以说考虑了平均应力修正的计算模型才更符合工程要求。

6 结论

(1）应用局部应力应变法来求解疲劳寿命时,缺口根部的局部应力和局部应变的计算精度直接影响最后计算寿命的精度,本文采用 Levenberg-Marquardt迭代法和二分法来求解非线性方程组,利用这两种算法编程求解的精度都达到了满意效果。

(2）求解应变-寿命曲线超越方程,必须采用计算机编程。二分法程序编写简单,通过二分法和迭代法的计算结果比较,证实其精度和效率也满足要求,易于工程应用。

(3）未考虑平均应力修正的应变寿命方程,计算出的疲劳寿命跟实际构件的试验寿命相差较大,而考虑了平均应力修正的应变寿命方程,计算结果与实际构件的试验寿命符合得较好。

(4）应用局部应力应变法来预测本文X型飞机结构一个带孔部件的寿命值时,取得了良好的效果,计算精度满足了工程要求。

[1]陈富来,帅健,丁可勤.烟气轮机叶片寿命的影响因素和评估方法[J].石油化工设备技术,2006,27(6）:43-48.

[2]舒陶,任宏光,郭克平.局部应力应变Neuber法与有限元求法的比较[J].弹箭与制导学报,2009,29(1）:267-270.

[3]姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2003.168-170.

[4]尚德广,李明,王大康,等.随机加载下缺口局部应力应变的弹塑性有限元计算[J].机械强度,2001,3(25）:25-27.

[5]聂宏,常龙.基于局部应力应变法估算高周疲劳寿命[J].南京航空航天大学学报,2000,32(1）:30-33.

[6]蔡力勋,叶裕明,高庆,等.Zr-4合金薄片材料的应变疲劳与寿命估算[J].西安交通大学学报,2004,38(1）:97-100.

[7]王东海,任慧龙,邹勇.平均应力修正对船体结构疲劳损伤计算的影响[J].哈尔滨工程大学学报,1998,19(1）:30-34.

[8]MORE.Jorge J.The Leven berg-Narquardtal gorithm:Implementation and theory[J].Lecture Notes in Mathe matics.1978,630:105-116.

Fatigue Life Evaluation on Plane Structural Parts with Holes through Local Strain Method

TONG Di-hua1, CHEN Zhi-wei2
(1.Beijing Institute of Aeronautical Materials,Beijing 100095,China;2.Beijing Aeronautical Technology Research Center,Beijing 100076,China）

The thesis introduces the work of calculating local stress and local strain by application of Levenberg-Marquardt's iteration method.As an usual mathematical method to solve super equation,Levenberg-Marquardt's iteration method has some disadvantages such as complicated program,low computing efficiency.Therefore,the paper aims to find out a comparatively simple,high efficient and high precision computing method.Through comparing and analyzing the efficiency and precision of dichotomy and Levenberg-Marquardt's iteration method by which solving strain life equation and local strain range,the thesis proves that the application of dichotomy is simple and applicable for the engineering.At last,through combination with the case of plane's drilled component,applying local stress strain method to calculate the parts'predictive life and comparing that result with the experimental life value,the paper concludes that strain life equation which concerns mean stress correction more fit for engineering requests.

local stress and local strain;Levenberg-Marquardt's iteration method;dichotomy;strain life equation;mean stress correction

10.3969/j.issn.1005-5053.2011.5.017

V223;V215.5

A

1005-5053(2011）05-0086-05

2011-02-23;

2011-07-05

童第华(1985—）,男,博士研究生,(E-mail）Tongdi133@163.com。

book=90,ebook=253