厚板射流冲击下淬火冷却的换热系数建模计算

邓运来, 贺有为, 曹盛强,2, 张新明

(1.中南大学材料科学与工程学院,长沙 410083;2.广西南南铝加工有限公司,南宁 530031）

厚板射流冲击下淬火冷却的换热系数建模计算

邓运来1, 贺有为1, 曹盛强1,2, 张新明1

(1.中南大学材料科学与工程学院,长沙 410083;2.广西南南铝加工有限公司,南宁 530031）

建立一种多喷嘴同时喷射淬火冷却的数学模型,通过实测冷却曲线分析计算厚板驻点区与紊流区换热系数分布规律,基于ABAQUS模拟软件模拟验证模型。结果表明:驻点与紊流点处的换热系数随时间分布是不均匀的,在10～20s内出现峰值,随后呈上下波动变化的规律;实测(或计算）试样心部与表面的冷却曲线与模拟的吻合较好,验证了多喷嘴同时喷射下的换热系数分布模型。

铝合金厚板;换热系数;ABAQUS模拟;射流冲击

中厚板生产过程中辊底喷淋淬火的换热过程极为复杂,在单射流及多射流作用下,表征换热冷却快慢的表面换热系数在喷射面上分布也极为复杂[1～3]。R.Gardon和 J.Cobonpue等[4]对圆形射流冲击换热的研究主要集中在平均换热系数和冲击面上点对点局部换热系数的变化,并且主要关注了冲击高度与射流直径之比对传热效果的影响。J.C.Akfirat等[5]在R.Gardon的基础上进行进一步的研究,他们测定了局部换热系数沿轴向和径向的变化规律,根据实验数据进行分析得出湍流度的变化发展是影响换热分布的主要原因,他们还发现了局部换热系数可能存在的二次峰值现象。而对于多射流,D.M.Kercher等[6]研究关于小尺寸矩阵冲击射流,研究喷嘴直径(D）在0.25～3.0mm之间,喷嘴间距与直径比(Xn/d）和冲击高度与直径比(Z/d）对换热的影响,得到换热系数主要取决于射流Re数和喷嘴间距与直径比Xn/d。国内许多学者[7～9]也研究了单射流及多射流下的换热过程,从流体力学角度出发建立Re数和Nu数与换热系数的关系,研究驻点区与紊流区换热模型,但模型都较为复杂,对于工程上生产航空航天用铝合金厚板的研究参考意义受到一定限制。

本研究以两组不同的喷嘴直径(D）、喷射压力(P）及相邻喷嘴距离(L）单面喷射7050铝合金厚板测得试样心部冷却曲线,建立换热系数分布模型并根据模型求得换热系数和表面温度随时间分布曲线。为验证所求的换热系数分布模型,本文基于ABAQUS模拟软件模拟分析了厚板单面喷射淬火过程的温度场,取试样表面与心部的冷却曲线分析其相对误差,以此来验证模型的正确性。

1 实验方法

在箱式电阻炉内将7050铝合金试样(规格为250mm×200mm ×100mm）加热至470℃后开始保温,使试样各部位温度均匀。K型热电偶安装在距驻点区和紊流区50mm远的心部(分别标记为TA和TB）。设置数据采样周期为0.2s。保温时间达要求后,将试样转移到自行设计的淬火装置中,转移时间在5～8s内。转移到装置上要保持试样淬火冷却端面中心与喷嘴中心在同一直线上,试样喷射表面与喷嘴的射流出口端面的距离(H）为25mm。通过电磁流量计调节好喷水流量进行喷射淬火。试样S1表面为射流冲击面,S2面用绝热板绝热,其余四个侧面在喷射淬火过程中用罩子盖住。本实验淬火装置的工作原理如图1所示。以L=50mm,D=4.0mm,P=200KPa(第一组）和 L=100mm,D=6.0mm,P=500KPa(第二组）两组参数单面喷射厚板淬火,所测得两组喷射工艺下TA和TB处冷却曲线如图2所示。

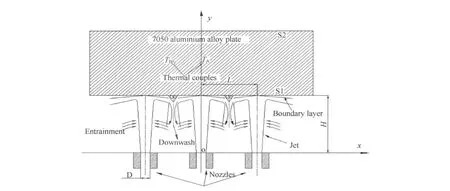
图1 3个喷嘴喷射工作原理图Fig.1 Schematic diagram of three nozzles jet impingement

图2 实测驻点区与紊流区心部冷却曲线Fig.2 Measured center cooling curve of stagnation and turbulent zone

2 换热系数求解模型的建立

2.1 换热系数反求模型建立

图3 无限大平板传热模型Fig.3 Heat model of infinite plate

本模型假设为无限大平板传热,视为无内热源、非稳态一维导热,从一维导热方程出发,利用分离变量法求出方程的解析解。引入新的变量过余温度θ(x,t）=T(x,t）-Tf。模型的假设为:假设传热如图3所示,为无限大平板传热;初始试样各处温度一致,均为470℃;冷却介质温度Tf在冷却过程中一直不变。建立的一点计算换热系数模型如下[10,11]:无内热源、非稳态导热数学模型

对于淬火一维传热模型进行求解,其边界条件和初始条件为:

边界条件为:

Tf,Tw,T0,T,θ分别为环境温度、表面温度、平板初始温度、板内温度和过余温度;

a,k,hw,t分别为热扩散率、热传导率、换热系数、淬火时间;

λn,δo,A分别为超越方程的前n级解、四分之一板厚、热交换表面面积。

根据1/4处C点温度曲线,结合式(2）和(3）计算出表面换热系数和表面温度随淬火时间的关系,其计算的结果见下图6和图7所示。

2.2 喷射面上换热系数分布

以圆形断面的喷嘴对7050铝合金厚板喷射淬火冷却时,冷却水介质受到射流冲击作用,其在喷射面上流动的方式是以圆形区域向四周展开的[12]。表征冷却快慢的表面换热系数在喷射面上随时间与空间的分布呈不均匀[2]。为了近似模拟研究厚板真实的冷却特性,在研究单喷嘴喷射下换热系数分布的空间模型时,本工作引入“正态分布模型”来研究换热系数在喷射面上的分布 。如图4所示,假设在试样的喷水端面上某个时刻的换热系数以喷淋区中心为旋转对称中心,在喷淋表面上呈二维分布。图4所示的平顶部分表示3倍喷嘴直径区域,该区域为射流强烈冲击影响区。而平顶外领域为二维面上服从正态分布的区域。其物理意义是喷淋水柱直接作用的部分区域上换热系数是相同的,其它换热面领域是不同的。

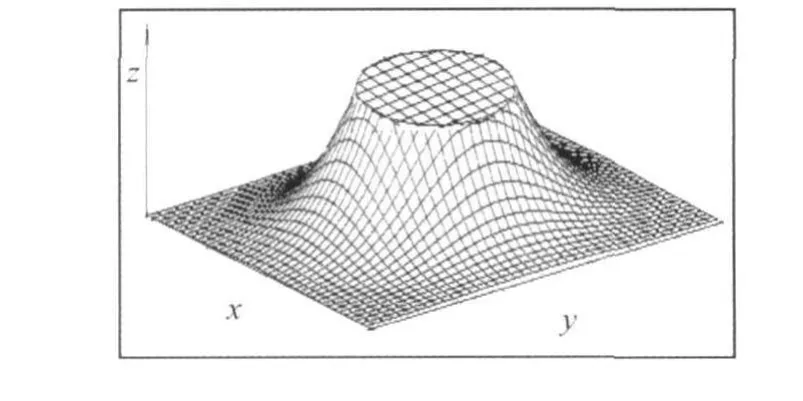
图4 淬火面上换热系数的二维分布Fig.4 The 2-d distribution of heat transfer coefficient at the quenching surface

如图4所示,以淬火面中心点为原点建立平面坐标系,边界为[-a,a](a是试样的半径或横截面边长）,淬火端面中心点换热系数为h0。淬火面中心接触水柱的强烈激冷区域是半径为r且换热系数大小为h0的圆面,并假设其余面上换热系数为类似正态分布,则换热系数的二维分布函数如式(4）所示。

结合本试验,厚板在三个喷嘴同时喷射淬火的条件下,当淬火介质水离开喷嘴后,受到水冲击压力的作用,冲击射击到喷射面上与喷射物体进行热交换。根据流体力学和高压水冲击原理[13],设计合理的水流冲击喷射面上换热系数分布划区模型。如下图5a,b所示,表示 L=100mm,D=6.0mm下中低压及高压的换热系数分布模型。中低压下喷射,因喷射水介质沿着喷射面运动,压力不大,紊流区基本可视为一条线,紊流影响区(E区）是一个很小的面,服从抛物线分布,另驻点区域内,冷却水以一个圆形的面展开形成强烈冲击区(C区）和射流影响区(D）区。高压下,紊流区受到沿各方运动的水的互相强烈干扰,形成一个小紊流区域(E区）。同理,可以设计L=50mm,D=4.0mm的喷射面上换热系数分布。

图5 喷射面上的换热系数分布模型(a）中低压;(b）高压A-驻点;B-紊流点;C-强烈冲击区;D-射流影响区;E-紊流影响区Fig.5 The model of heat transfer coefficient distribution at spraying surface(a）medium and low pressure;(b）high pressureA-stagnation point;B-turbulent point;C-intense impact t zone;D-jet affected zone;E-turbulence affected zone

3 模型求解验证及讨论分析

3.1 换热系数与时间关系曲线

测得图2所示驻点区与紊流区心部冷却曲线,建立温度与时间的关系数据。根据冷却曲线和上节建立的换热系数反求模型计算出表面驻点和紊流点(分别为图5中A与B处标识）处的换热系数随时间分布的关系曲线,见图6所示。从图6中可以看出,不同的喷射参数L,D,P对厚板表面的冷却是不同的,但总体表现为换热系数随时间的变化是在一定的时间内(10～20s）出现峰值,淬火后期(60s后）换热系数上下波动变化。而根据模型及计算出的换热系数计算得到表面温度的分布如下图7c,d所示,从图7c,d中可以看出,表面温度出现“回升”现象。这是因为淬火过程中,先后经历汽膜沸腾、过渡沸腾、成核沸腾和强制对流换热四个过程[13]。开始淬火时,试样端面温度较高,水被迅速汽化成气泡,积聚增大,这些蒸汽膜使得试样内部热量无法及时排除,导致换热系数较小。当随着淬火时间的增加,端面温度骤降后,进入过渡沸腾阶段,气泡聚合成汽膜的趋势降低,换热系数增大。当某一时刻,换热进入了核态沸腾阶段,此阶段下气泡会二次形核、长大,吸收大量的热量,新的液体也会不断流向原来的气泡位置,出现了强烈的换热效应,换热系数迅速增大,出现了峰值。而随后当端面温度下降到低于100℃时,处于强制对流换热,换热系数开始变小。但同时材料导热快慢与传导系数、比热容及密度有关,试样上端不断地有热量沿着喷射端面传递,新的液体介质不断流入,使得表面温度回升。

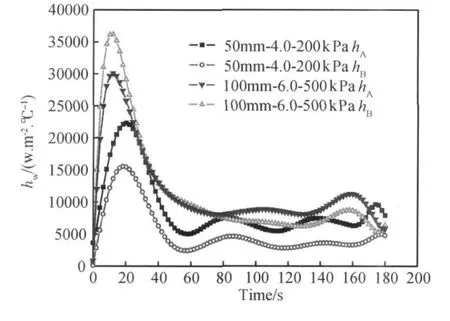
图6 换热系数与时间关系曲线Fig.6 Rlation curves of heat transfer coefficient and time

从图6中还可以看出,不同L,D,P下喷射厚板淬火冷却,表面驻点与紊流点冷却是不同的。以第一组工艺喷射冷却,驻点A处换热系数hA在18s时出现峰值,峰值为22311W.m-2.℃-1,较紊流点B处的hB(hB的峰值为15346 W.m-2.℃-1）大。而第二组工艺喷射冷却的紊流点换热系数峰值比驻点的大。这是因为受射流冲击作用,当L/D=25时,换热系数在喷射面上的分布是驻点处最大,远离驻点则变小,当两股射流在紊流处干扰较小时,则紊流点处的换热系数峰值就小;当L/D=16.7时,换热系数除了呈图4的二维分布外,在紊流处,两股射流冲击强烈,产生涡流互渗,强烈的干扰速率场使得层流向湍流过渡,这时紊流点的换热系数峰值就比驻点的大。

3.2 模型求解验证及分析

基于有限元软件ABAQUS6.8平台对单面喷射7050铝合金试样进行温度场模拟,模拟参数中的导热系数λ、比热容 c和密度 ρ均随温度变化[15],见表1。初始温度整体为470℃,淬火水介质温度为21℃,网格单元为C3D8RT实体三维8节点热力耦合减缩积分单元,为适应步长设定出最大和最小温差分别为10℃,1℃[16],淬火时间为180s。

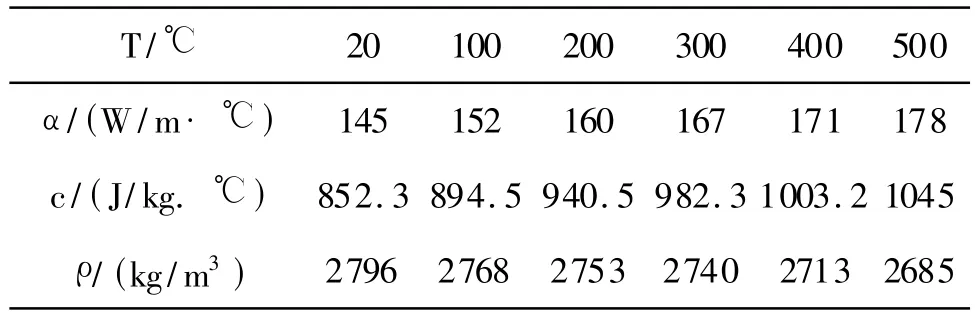
表1 各热物性参数随温度变化[15]Tab.1 Thermal properties parameters change with temperature

建立的换热系数在喷射面上分布的模型经ABAQUS有限元软件包的FILM[17]接口编写程序后输入,空气换热系数随表面温度变化按文献[18]加载。模拟求得的试样驻点区与紊流区心部及表面的冷却曲线见下图7所示。相对误差分析定义为下式5所示。

如图7a和b所示,表示以第一组和第二组试验参数喷射厚板冷却的心部实测与模拟的冷却曲线。从图7a和b中可以看出,以第一组工艺喷射淬火,驻点区心部较紊流区心部冷却快,而第二组工艺喷射下,紊流区心部冷却较驻点区的快。比较实测与模拟的心部冷却曲线,当以第一组工艺喷射时,前60s淬火的实测与模拟的冷却曲线吻合最好,淬火后期驻点区A处的实测与模拟的相对误差增大,最大的相对误差为11.2%;而以第二组喷射工艺喷射时,实测与模拟的冷却曲线见下图7b所示,淬火前140s实测与模拟的曲线吻合最好,淬火140s后驻点区心部的相对误差有所增大,但紊流区的相对误差较小。根据所建立的模型计算表面冷却曲线与模拟的冷却曲线见图7c和d所示。从图7c和d可以看出,以第二组喷射工艺喷射冷却,所计算的驻点A处和紊流点B处的表面冷却曲线与模拟的表面冷却曲线吻合最好,最大的相对误差出现在淬火120s和140s处,相对误差总体小于6%。而以第一组喷射工艺淬火冷却,驻点A处与紊流点B处的计算与模拟相对误差在淬火60s后吻合较好,在20～40s间误差相对较大。但总体上无论是以第一组还是第二组工艺喷射计算表面温度与模拟的吻合较好。

以本工作建立的换热系数计算模型所求得的换热系数作为加载,基于计算机模拟软件ABAQUS模拟得到的冷却曲线与实测(或计算）的分析可知,建立的数学模型可以应用于多喷嘴同时喷射厚板淬火的研究领域并指导生产,也可以为计算机模拟厚板淬火过程的温度场及残余应力/应变场所需换热系数的加载提供参考。

图7 驻点区与紊流区心部及表面冷却曲线比较Fig.7 Compared the heart and surface cooling curves in stagnation and turbulent point(a）L=50mm in heart;(b）L=100mm in heart;(c）L=50mm at surface;(d）L=100mm at surface

4 结论

(1）建立多喷嘴同时喷射下换热面上换热系数分布模型,根据模型分析多喷射同时喷射下换热系数随时间的分布规律是:驻点A处和紊流点B处的换热系数随时间在10～20s内出现峰值,随后呈上下波动变化规律;淬火过程中,驻点A处与紊流点B处的换热系数分布不同。

(2）通过模拟分析试样单面淬火的温度场,比较分析试样表面及心部的冷却曲线得到,无论是心部还是表面温度的实测(计算）与模拟的数据都比较吻合。依此验证了所建立的换热系数分布模型的正确性,为工程研究提供参考。

[1]MANSOO C,HAN S Y.Measurements of impinging jet flow and heat transfer on a semi-circular concave surface[J].Heat and Mass Transfer,2000,1811-1822.

[2]周定伟,马重芳,任玉涛.圆形浸没射流冲击下有关压力梯度的理论分析[J].西南交通大学学报.1999,33(7）:54-57.

[3]BUDDHIKA N.A numerical study of heat transfer performance of ossillatory impinging jets[J].International Journal of Heat and Mass Transfer,2009,(52）:396-406.

[4]GARDON R,COBONPUE J.Heat transfer between a flat plate and jets of air impinging on it[J].Internationnal Developments in Heat Transfer.ASME,New York.1962.454-460.

[5]GARDON R,AKFIRAT J C.The role of turbulence in determining the heat transfer characteristics of impinging jets[J].Int J Heat Mass Transfer,1965.8:1261-1272.

[6]KERCHER D M,TABAKOFF W.Heat transfer by a square array of round air jets impinging perpendicular to a flat surface including the effect of spent air[J].Transactions of the ASME Journal of Engineering for Power,1970:73-82.

[7]马重芳,陈永昌.自由表面二维射流冲击在小尺寸加热面上的局部换热特性[J].北京工业大学学报,2000,26(3）:59-62.

[8]赵耀华,马重芳.圆形自由射流冲击任意热流密度平板时的换热分析[J].北京工业大学学报,1989,15(3）:7-13.

[9]陈庆光,徐忠,张永建.湍流冲击射流流动与传热的数值研究进展[J].力学进展,2002,32(1）:92-108.

[10]张靖周,常海萍.传热学[M].北京:科学出版社,2009:70-88.

[11]廖凯,吴运新,张园园.铝合金厚板淬火表面换热系数的离散解析求法[J].材料热处理学报,30(1）:192-196.

[12]牛珏,温冶,王俊升.圆形喷口紊流冲击射流流动与传热过程数值模拟[J].冶金能源,2007,26(1）:16-20.

[13]薛胜熊.高压水射流技术与应用[M].北京:机械工业出版社.1998:8-20.

[14]俞景禄,魏季和.冶金中的传热传质现象[M].北京:冶金工业出版社,1981:296-299.

[15]MUAMMER K,JOHN C,TAYLAN A.Prediction of residual stresses in quenched aluminum blocks and their reduction through cold working processes[J].Journal of Materials Processing Technology,2006,174:342-354.

[16]李辉平,赵国群,贺连芳.时间步长对淬火过程温度场和组织场模拟精度的影响.金属热处理[J].2007,32(2）:60-64.

[17]ABAQUS Analysis User's Manual,User Subroutines,FILM,Section 25.2.6.

[18]郭世贵.7050铝合金材料喷淋淬火的试验与模拟研究[D].长沙:中南大学.2010.

Model Calculation of Heat Transfer Coefficient of Quenched Cooling under Jet Impingment Plate

DENG Yun-lai1, HE You-wei1, CAO Sheng-qiang1,2, ZHANG Xin-ming1
(1.School of Materials Science and Engineering,Central South University,Changsha 410083,China;2.Guangxi Alnan Aluminium Fabrication CO.LTD,Nanning 530031,China）

The quenched cooling heat transfer process of the thick plate by multi-nozzle jet impinging is extremely complicated,thus it is difficult to establish a model of the surface heat transfer coefficient distribution,which reveals the speed of the heat transfer on the jet impinging surface.In this paper,the mathematical model of multi-nozzle jet simultaneously impinging quenched cooling has been established,coefficient distribution law at the stagnation and turbulent zone has been calculated by actual measurement of the cooling curve and has been verified based on the ABAQUS simulation software.The results show that the coefficient distribution at the stagnation and turbulent zone is uneven over time,and the peak appeared within10 to 20 seconds,and then comes to the variation of the next waves.The actual measurement(or calculation）of the cooling curves at the sample's center and surface is at a very good match state with that of simulation,therefore it verifies the heat transfer coefficient distribution model under the multi-nozzle jet simultaneously impinging.

aluminum alloy plate,heat transfer coefficient,ABAQUS simulation,jet-impinging

10.3969/j.issn.1005-5053.2011.5.005

TG 249.1;TG146.2

A

1005-5053(2011）05-0023-06

2010-11-12;

2011-03-31

国家重点基础研究计划资助项目(2005CB623700）

邓运来(1969—）,男,博士,副教授;主要从事有色金属材料成型技术的研究,(E-mail）dengylcsu@126.com。