基于UKF和线性优化的改进粒子滤波算法＊

黄双华 白海东），2） 柯 斌 江艳阳）

（海军工程大学1） 武汉 430033）（武汉军械士官学校2） 武汉 430075）（海司四部雷达处3） 北京 100000）

1 引言

针对非线性问题，常用的算法有扩展卡尔曼滤波（EKF）、不敏卡尔曼滤波（UKF）、粒子滤波等，其中粒子滤波不受线性化误差和高斯噪声假定的限制，适用于任何环境下的任何状态模型和量测模型。

1993年由Gordon［1］等提出的一种新的基于SIS的Bootstrap非线性滤波方法，奠定了粒子滤波算法的基础。近年来提出的许多非线性滤波新方法，都是基于SIS滤波思想，根据重要性函数的不同选择和重采样方法的不同，可以对粒子滤波器进行改进。

本文将对重要性函数选择的改进方法和一种新的重采样方法结合起来，提出了基于UKF［2］和线性优化［3～4］的粒子滤波算法。

2 粒子滤波

2.1 粒子滤波算法概述

粒子滤波算法是一种基于Monte Carlo仿真的最优回归贝叶斯滤波算法，这种滤波方法的基本思想是用随机样本来描述概率分布，这些样本被称为“粒子”，然后在测量的基础上，通过调节各个粒子权值的大小和样本的位置，来近似实际的概率分布，并以样本的均值作为系统的估计值。随着样本（粒子）数目的增加，粒子的概率密度函数逐渐逼近状态的概率密度函数，粒子滤波估计即达到了最优贝叶斯估计的效果。

2.2 重要概率密度函数

在粒子滤波中，重要性概率密度函数［5～6］分布与目标概率分布是否接近，将直接影响到跟踪的精度。最优的重要概率密度函数就是后验分布函数p（xk｜z1：k）本身，但是通常情况下很难直接从p（xk｜z1：k）抽样得到样本。在标准粒子滤波算法中，为了求解方便，一般取重要概率密度函数为先验概率分布，即：q（xk｜xik－1，zk）＝p（xk｜xik－1）。

2.3 重采样

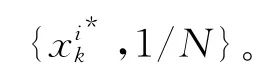
2.4 标准粒子滤波算法存在的问题

标准粒子滤波算法存在的最大问题是粒子退化现象。粒子退化意味着大量的计算资源都被用来更新那些对q（xk｜z1：k）的估计几乎没有作用的粒子上。

针对此问题，最直接的方法就是使用大量的粒子数目，因为粒子滤波的理论基础是大数定理，采样足够多的粒子，必可以使样本均值以概率1趋于数学期望。但实际上，这是不现实的，随着粒子数的增大会增加系统的资源开销，影响算法的实时性。因此通常采样的两种方法是：改进重要概率密度函数和改进重采样方法。

3 改进的粒子滤波

3.1 不敏卡尔曼滤波［7］（UKF）

UKF对状态向量的PDF进行线性化，表现为一系列选取好的δ采样点。这些δ采样点经过任何非线性系统的传递后得到的均值和协方差都能够精确到真实后验分布的二阶矩，因此可以很容易的应用该算法得到极为接近真实后验分布的重要概率密度函数。

3.2 线性优化

线性优化重采样克服了标准粒子滤波算法中重采样过程中由于去掉权值小的粒子的同时，只是简单的复制权值大的粒子而导致的粒子多样性的丧失。线性优化重采样的基本思想是：在需要复制某个粒子时，通过将该粒子和被抛弃的粒子进行适当的线性组合而产生一个新的采样点。

线性优化重采样具有的优点是：不存在重复的粒子，保证了粒子的多样性，小权值的粒子未被完全抛弃，仍以一定的概率参与对状态向量的估计。

3.3 UKF和线性优化的粒子滤波

将UKF和线性优化重采样的思想结合起来，产生本文的改进粒子滤波算法。该算法步骤为：

1）初始化：k＝0。

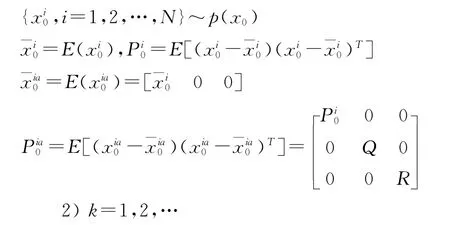
重要性采样：i＝1，2，…，Ns，使用UKF算法更新粒子。选取粒子：

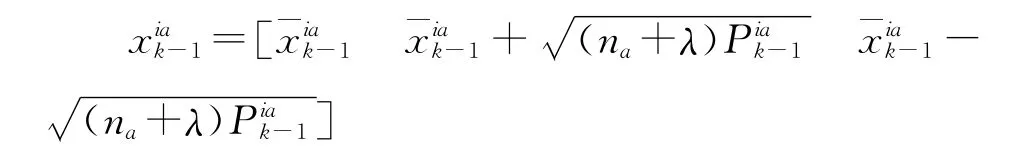
其中，na＝nx＋nw＋nv

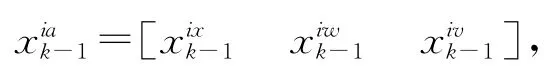
时间更新：

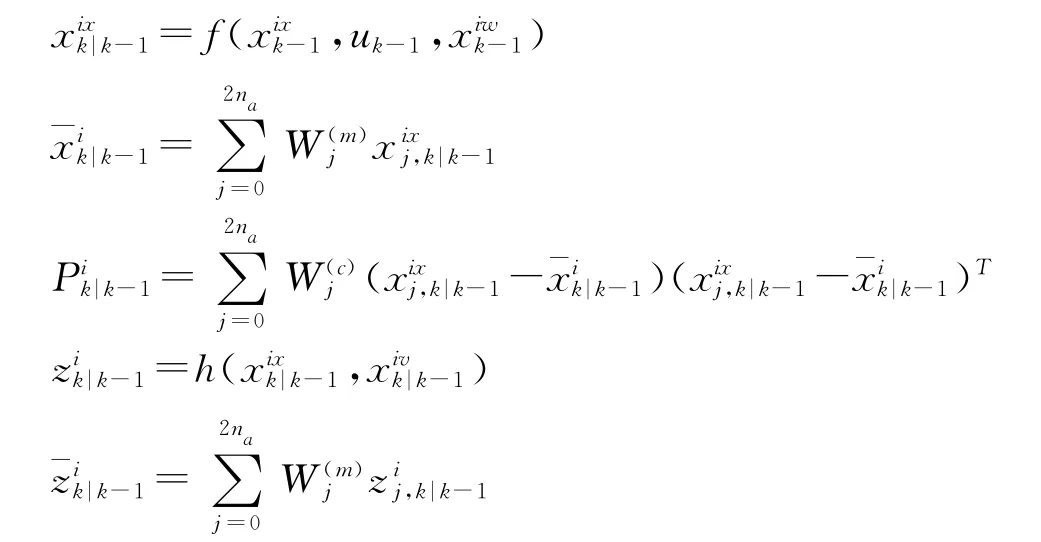
测量更新：

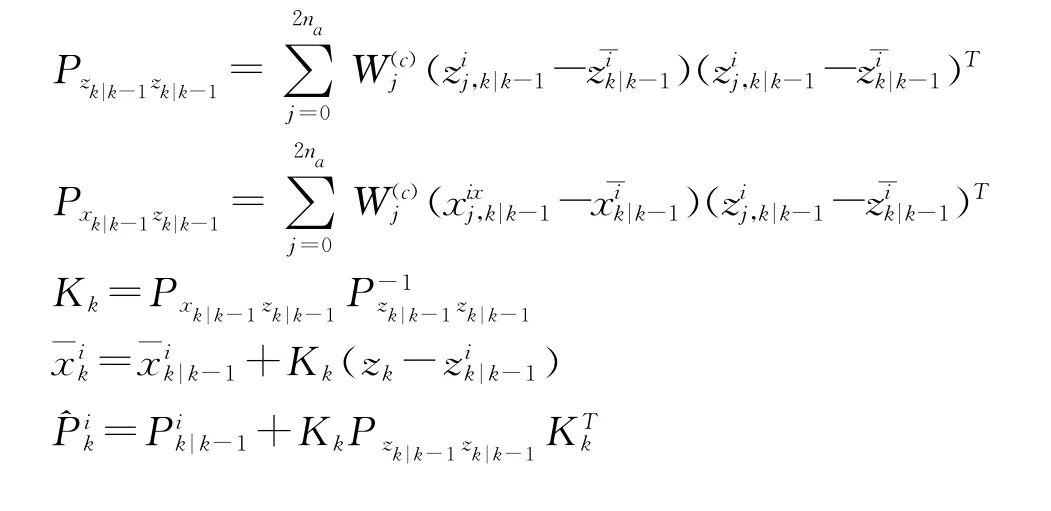
采样粒子：

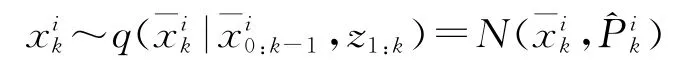
其中，N（·）表示高斯函数。计算权值：

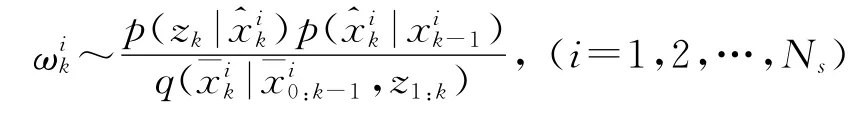
3）线性优化重采样：

比较粒子的权值：

按照xn＝xα＋L（xα－xβ）进行线性优化以产生新的粒子。式中xn表示新粒子，xα表示复制组的粒子，xβ表示抛弃组的粒子，L为（xα－xβ）的合适步长。L按下式选取：

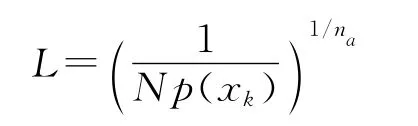
4）输出：

协方差估计：

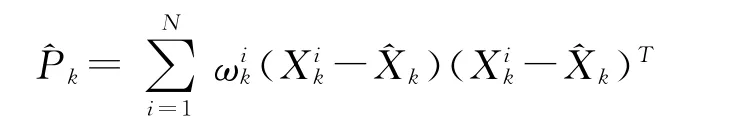
5）判断是否结束，是则退出本算法，否则返回到步骤2）。

4 仿真验证

本文应用标准粒子滤波算法和改进的粒子滤波算法分别对单变量非静态增长模型（UNGM模型）进行仿真分析，该模型的状态方程和量测方程如下：

状态方程：

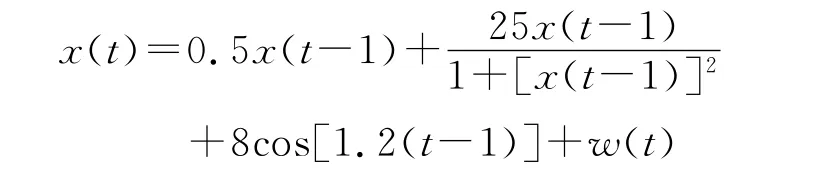
式中，w（t）、v（t）为零均值高斯噪声。

取N＝100，初始值：Q＝1，R＝1，P＝2，x＝0.1。进行100次Monte Carlo仿真，得到的状态估计曲线图如下。

由图1和图3可以看出改进的粒子滤波算法较标准粒子滤波算法有非常明显的改进效果。图2和图4分析可知，改进的粒子滤波算法较UPF

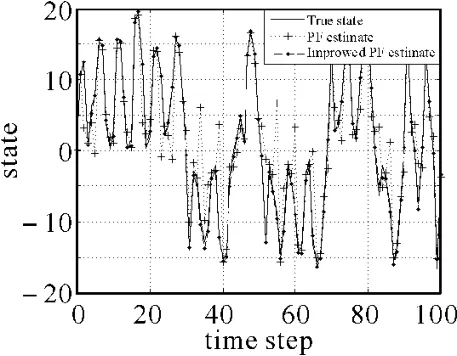
图1 PF与Improved PF的状态估计

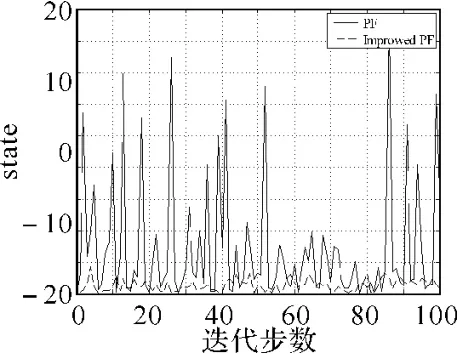
图2 PF与Improved PF的均方误差曲线

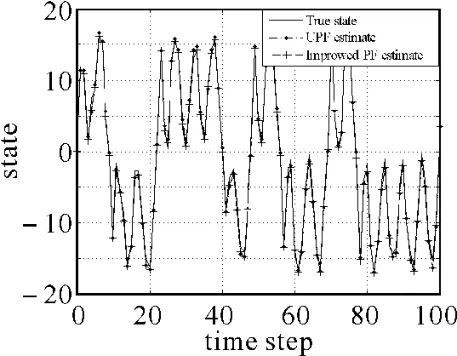
图3 UPF与Improved PF的状态估计

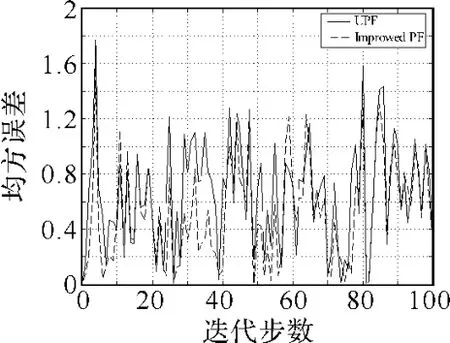
图4 UPF与Improved PF的均方误差曲线

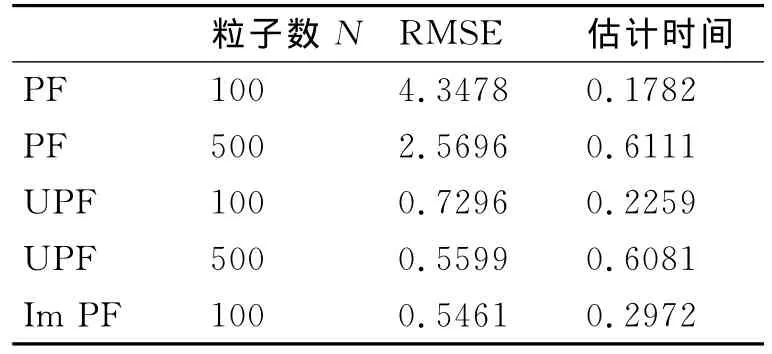
表1 三种粒子滤波器的性能比较

5 结语

本文通过结合不敏卡尔曼滤波算法和线性优化的思想，提出了一种新的改进粒子滤波算法，通过仿真验证了算法的有效性和实时性。

［1］Gordon N，Salmond D.Novel approach to nonlinear and non-Gaussian Bayesian state estimation［J］.Proc of Institute Electric Engineering，1993，140（2）：107～113

［2］Julier S J，Uhlmann J K，Durrant-Whyten H F.A New Approach for Filter Nonlinear System［DB／OL］.［2009-02-21］.http：／／ieeexplore.ieee.org／servlet／opac？punumber＝5209213

［3］朱志宇.粒子滤波算法及其应用［M］.北京：科学出版社，2010，6

［4］邹国辉，敬忠良，胡洪涛.基于优化组合重采样的粒子滤波算法［J］.上海交通大学学报，2006，40（7）：1135～1140

［5］Doucet A.On Sequential Simulation-based Method for Bayesian Filtering［R］.Technical Report Dept Engi CUED-F-TR310.Cambridge：Cambridge University，1998

［6］Liu J S，Chen R.Sequential Monte Carlo Methods for Dynamic Systems［J］.Journal of the American Statistical Association，1998，93（443）：1032～1044

［7］何友，修建娟，张晶炜，等.雷达数据处理及应用［M］.北京：电子工业出版社，2009

［8］杨璐，李明，张鹏.一种新的改进粒子滤波算法［J］.西安电子科技大学学报（自然科学版），2010，37（5）：862～865

［9］王来雄，黄土坦.一种新的粒子滤波算法［J］.武汉大学学报（工学版），2006，39（1）：118～120

［10］曲彦文，张二华，杨静宇.改进的无迹粒子滤波算法［J］.控制理论与应用，2010，27（9）：1152～1158

［11］张念慈，钟珞，余昌瑾.改进的粒子滤波算法在多目标跟踪中的应用研究［J］.计算机与数字工程，2009，37（12）

［12］饶文碧，王君，雷育华.基于粒子滤波的机动目标跟踪算法仿真研究［J］.计算机与数字工程，2009，37（3）

［13］胡士强，敬忠良.粒子滤波算法综述［J］.控制与决策，2005，20（4）：361～365