低复杂度多进制LDPC码译码算法研究*
杨雪飞 李 瑞
(海军装备研究院1) 北京 100161)(海军装备部2) 北京 100161)
1 引言
自从LDPC(Low-Density Parity-Check)码被重新发现以后,它就以接近香农限的优越性能受到极高的重视[1]。多进制LDPC码比RS码更胜一筹之处在于它的FFT-QSPA译码算法比RS码的AHD BM (Algebraic Hard-Decision Berlekamp-Massey)算法和 ASD KV(Algebraic Soft-Decision Kotter-Vardy)算法更有效率。RS码由于构造简单、代数结构已知、良好的最小距离,仍然是最好的一类多进制码型。不过目前仍然没有一种有效的软判决译码算法在实际应用的复杂度内达到较大的编码增益。本文针对低复杂度的多进制LDPC码编译系统给出了一种联合构造—编码—译码的方案,即使用准循环结构的校验矩阵,由此带来编码的优势—只需采用简单的循环移位累加寄存器(CSRAA)单元来进行编码,其复杂度与码字的校验比特成正比;译码采用性能和复杂度折衷的FFT-QSPA算法。
2 具有准循环结构的多进制LDPC码的构造
多进制LDPC码的构造主要是校验矩阵H的设计与构造,本文介绍有限域法,这种方法构造的码具有循环或者准循环结构[7~11]。
令α为GF(q)域本原元,那么α-∞=0,α0=1,α,…,αq-2是 GF(q)域的全部元素。非零元素αi(0≤i≤q-2)的位置向量z(αi)=(z0,z1,…,zq-2),其中zi=αi,其余q-2个元素为0。
在GF(q)域下,用有限几何和有限域方法构造多进制LDPC码需要构造一个基矩阵W。

W须满足乘α-行约束1)和2):1)对于0≤i<m,0≤k,l<q-1并且,k≠l,αkwi与αlwi至少有n-1个位置不同;2)对于0≤i,j<m,i≠j,且0≤k,l<q-1,αkwi与αlwj至少n-1个位置不同。
对W的每一个wi,j进行水平和垂直方向的扩展[13],得到 Ai,j:

从而得到校验矩阵m(q-1)×n(q-1)维矩阵H:
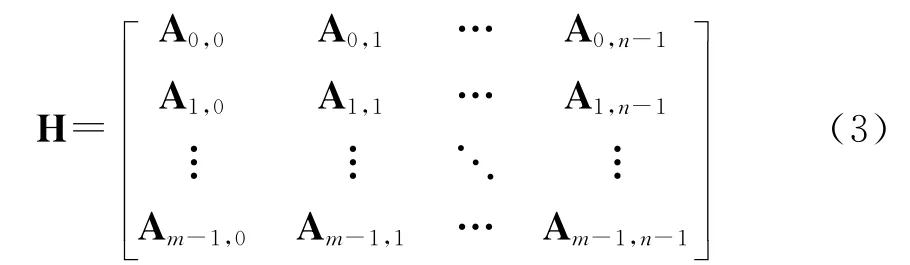
使用有限域构造满足乘α-行约束1)和2)的基矩阵时,可以用加群、乘群和循环群来构造。以加群构造为例,令α为GF(q)域本原元,构造如下基矩阵W:

3 低复杂度多进制LDPC译码算法
3.1 基本概念与初始化过程
如图1所示,多进制LDPC译码因子图包含变量节点(顶部圆块)、校验节点(底部圆块)、置换节点和重排节点。其中置换节点将置信度向量进行循环移位,重排节点将置信度向量按照对应的a∈GF(q)递增顺序排列。

图1 多进制LDPC译码因子图
定义如下变量:{Vpv}v=1,…,dv表示进入度为dv的变量节点的置信度,{Uvp}v=1,…,dv表示从这一变量节点出来的置信度。下标pv表示置信度由转置节点传递到变量节点,vp则表示其反方向;同样{Upc}c=1,…,dc表示进入度为dc的校验节点的置信度,{Vcp}c=1,…,dc表示进入这一校验节点的置信度。


其中vi,c,vi,s是两个独立的高斯白噪声。

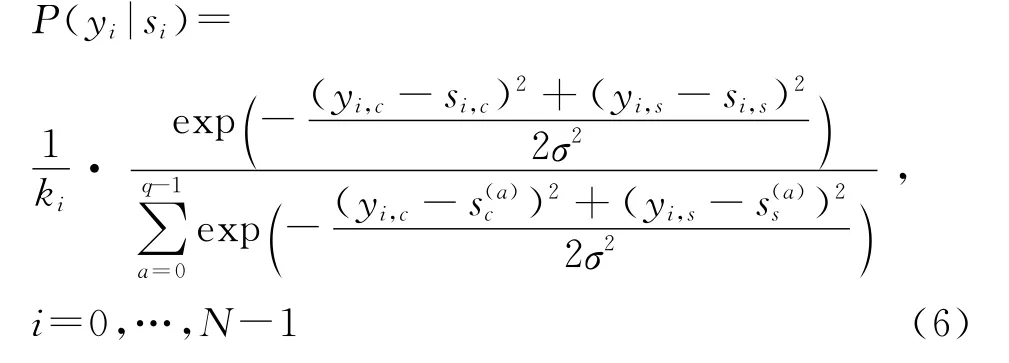
其中ki=P(si)/2πσ2P(yi),为一常数。
当采用BPSK调制时,映射方式是si=2ci-1(i=1,…,N),初始化概率为:
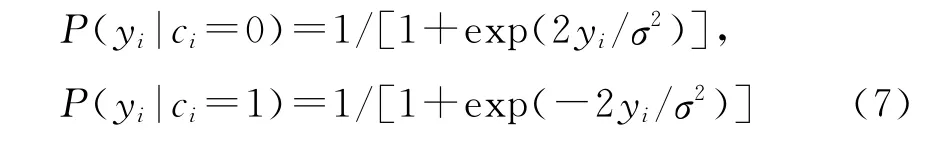
3.2 低复杂度的FFT-QSPA算法
采用BPSK调制时,根据接收信道值yi计算信道的转移概率,得到初始化概率:


其中ak是a二进制表示的第k个比特,置信度L=(L1,L2,…,LN)。
令 U[i1,…,ip]为p维张量,其中(i1,…,ip)∈{0,1}p。U[i1,…,ip]在 GF(2p)中 FFT 运算规则如式(9)所示:
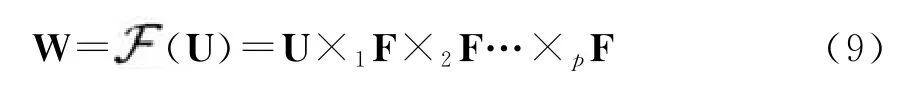
张量乘法Z=U×kF定义如式(11)和式(12)所示:

采用对数域运算的FFT-QSPA算法具体步骤如下:
第一步:初始化
令Uvp=L,其中L元素的取值由式(8)得到;
第二步:校验节点更新
(S1):移位步骤
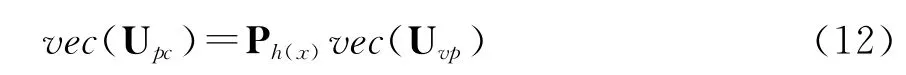
Ph(x)实际上就是将所有的值进行循环移位。对于反方向的移位步骤,可以用P-1h(x)表示;
(S2):重排
将置信度按照对应的a∈GF(q)递增顺序排列;
(S3):FFT

第三步:变量节点更新

第四步:尝试译码
此时硬判决

3.3 复杂度分析
对于(N,K)规则 GF(q)-LDPC码,使用本文给出的基于查找表法的低复杂度多进制LDPC的FFT-QSPA译码算法时,乘除运算均转化为加法运算,每次迭代的每一步骤运算量如表1所示。

表1 每次迭代运算量
4 仿真与分析
本文的仿真基于AWGN信道,发送端采用BPSK调制,所构造的多进制LDPC码与RS码在码率和码长相当的情况下进行比较,多进制LDPC码使用给出的低复杂度FFT-QSPA算法进行译码,最大迭代次数为50次,RS码采用硬判决算法进行译码。
用有限几何方法在GF(28)下构造校验矩阵H,选取dv=dv=16,那么H的零空间给出码率为0.68、最小距离为17的(255,175)QC-LDPC码。由图2可以看出,在BER为10-5处,(255,175)GF(28)-LDPC码比(255,175)RS码有1.55dB的编码增益;在BLER为 10-2处,(255,175)GF(28)-LDPC 码 比(255,175)RS码有1.76dB的编码增益。

图2 (255,175)GF(28)-LDPC码与(255,175)RS码的性能曲线
用有限域方法在GF(24)下构造校验矩阵H,选取dv=3、dc=6,那么H的零空间给出码率为0.57、最小距离为4的(90,51)QC-LDPC码。由图3可以看出,在 BER 为10-5处,(90,51)GF(24)-LDPC码比(90,50)RS码有3dB的编码增益;在BLER为10-2处,(90,51)GF(24)-LDPC码比(90,50)RS码有2.79dB的编码增益。

图3 (90,51)GF(24)-LDPC码与(90,50)RS码的性能曲线
从图2和图3可以清楚地看到,多进制LDPC码与RS码在具有相同码率,相同比特帧长的情况下,性能均要比RS码优越。

表2 每次迭代的计算次数
GF(qm)-LDPC码使用FFT-QSPA译码算法时,由表1可知每次迭代的计算次数为o(Ndvqmlogqm)。表2给出了多进制LDPC码与RS码译码时每次迭代的计算次数。5次迭代时(255,175)RS码每次迭代的计算次数是(255,175)LDPC码的2.5倍,(90,50)RS码是(90,51)LDPC码的24倍。50次迭代时,(90,50)RS码每次迭代的计算次数是(90,51)LDPC码的2.4倍。50次迭代时,(255,175)LDPC采用有限几何方法在 GF(28)域下构造,行重较大,因此计算量大于(255,175)RS码,可以通过减少迭代次数来降低计算次数,当迭代次数下降到5次时,仿真表明其性能损失较小且仍然比RS码性能优越。因此,译码算法的复杂度还与校验矩阵H的构造有关,N与dv也是制约其复杂度的因素。如果要获得低复杂度,译码算法不但要考虑译码本身的复杂度,还要考虑校验矩阵H的构造,才能得到一种低复杂度的译码算法。
5 结语
多进制LDPC码译码算法复杂度是制约其实用的一个重要因素,为了降低多进制准循环低密度奇偶校验(QC-LDPC)码译码的复杂度,给出了一种低复杂度多进制LDPC码的译码算法,其准循环结构校验矩阵的构造采用的是基于有限域和有限几何的方法,这些方法可以实现多进制LDPC的线性编码。通过仿真验证本文构造的多进制QCLDPC码不但明显优于相同参数的RS码,更重要的是复杂度大大降低。
[1]R.G.Gallager.Low density parity check codes[J].IRE Trans.Inform.Theory.,1962,1(8):21~28
[2]M.C.Davey,D.J.C.Mackay.Low-density parity check codes over GF(q)[J].IEEE Commun.Lett.,1998,2(6):165~167
[3]D.J.C.Mackay,M.C.Davey.Evaluation of Gallager codes of short block length and high rate applications[J].Proc.IMA International Conf.Mathematics its Applications:Codes,systems Graphical Models,2000:113~130
[4]H.Song,J.R.Cruz.Reduced-complexity decoding of Q-ary LDPC codes for magnetic recording[J].IEEE Trans.Magn.,2003,39(3):1081~1087
[5]H.Wymeersch,H.Steendam,M.Moeneclaey.Logdomain decoding of LDPC codes over GF(q)[J].Proc.IEEE Int.Conf.Commun.,2004:772~776
[6]D.Declercq,M.Fossorier.Decoding algorithms for nonbinary LDPC codes over GF(q)[J].IEEE Trans.Commun.,2007,55(4):633~643
[7]Lingqi Zeng,Lan Lan,Ying Yu Tai,et al.Construction of Nonbinary Quasi-Cyclic LDPC Codes:A Finite Field Approach[J].IEEE Trans.Commun.,2008,56(4):545~554
[8]Shumei Song,Bo Zhou,Shu Lin,et al.A Unified Approach to the Construction of Binary and Nonbinary Quasi-Cyclic LDPC Codes Based on Finite Fields[J].IEEE Trans.Commun.,2009,57(1):84~93
[9]Lingqi Zeng,Lan Lan,Ying Yu Tai,et al.Construction of Nonbinary Cyclic,Quasi-Cyclic and Regular LDPC Codes:A Finite Geometry Approach[J].IEEE Trans.Commun.,2008,56(3):378~387
[10]Bo Zhou,Jingyu Kang,Ying Yu Tai,et al.High Performance Non-Binary Quasi-Cyclic LDPC Codes on Euclidean Geometries[J].IEEE Trans.Commun.,2009,57(5):1298~1311

