罗兰C地波传播的ASF修正研究＊

徐务农 边少锋 陈永冰

（海军工程大学电气与信息学院1） 武汉 430033）（海军902厂2） 上海 200083）

1 引言

罗兰C系统通过测量频率为100kHz的地波信号从发射台到用户接收机之间的传播时间TOA（圆圆定位）或时间差TD（双曲线定位）来测定它们之间的距离或距离差，从而实现用户定位。罗兰C导航仪的定位解算是建立在地波信号以固定速度（在海水中的传播速度）、以最短路径（大圆距离）传播的假定基础之上的。由于罗兰C地波信号的传播路径并不是大圆弧，传播介质也并不全为海水，因此，这两条假设都带来了误差，这种误差称为传播误差。目前，与传播路径有关的传播误差成为罗兰C定位误差的主要成分。对传播误差进行理论和实测研究，对提高罗兰C的定位精度具有重要的意义。

2 地波传播时延与ASF

根据电磁波传播理论，对于任何地波路径，信号电场的垂直分量可表示为［1］：

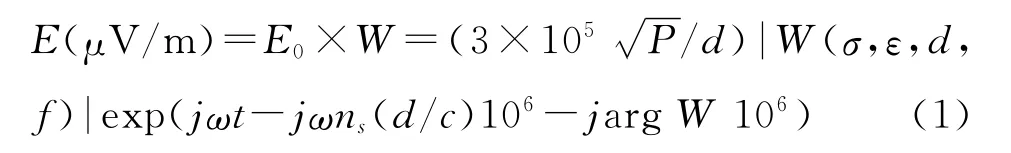
罗兰C地波信号从发射台到用户接收机的传播时间为：

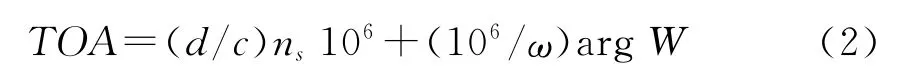
记PF为一次相位因子，即信号在大气中传播的时延；SF为二次相位因子，即海水相对大气的附加时延；ASF为附加二次相位因子，即大地相对海水的附加时延。则PF＝（d／c）ns106，SF＋ASF＝（106／ω）argW，从而

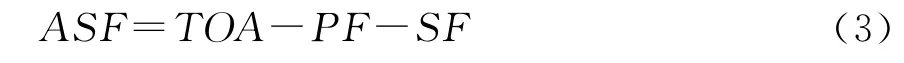
其中，E0为电场的复振幅，对应的相位为一次时延；W为地波衰减函数，对应的相位为二次时延（SF＋ASF）；c为自由空间中的光速（299792.458km／s）；d为 地 波 传 播 路 径 的 长 度（km）；ns为沿地波路径地表面附近大气折射指数；P为发射天线的辐射功率（kW）；σ为大地电导率；ε为相对大地介电常数；f为罗兰C信号的频率。

3 地波衰减函数的计算

由于PF和SF可以准确预算，由式（3）可知，要得到ASF，关键是要得到地波信号的传播时延TOA，而计算传播时延的核心是求解地波衰减函数。地波衰减函数与地面电导率和相对介电常数以及传播路径上大气折射指数有关，也与地面曲率和地形等因素有关。在工程计算中，按传播路径上介质电特性分布和地形高程变化，把传播路径分为均匀光滑路径、分段均匀光滑路径和非均匀光滑路径。对于均匀光滑路径，采用留数级数法计算，近距离用平面模型，远距离用球面模型。100kHz电波平面模型和球面模型的分界距离取为70km，可以保证两种模型的计算结果在分界处能够光滑衔接［2］。对于分段均匀光滑路径，按电特性和地形特征把路径分成若干段，用等效电参数法把地形的影响等效为电参数的影响，然后采用米林顿法计算。对于复杂的非均匀光滑不规则路径，则用积分方程方法来处理。

2）｜q｜≤1时，地波衰减函数W的计算公式为：

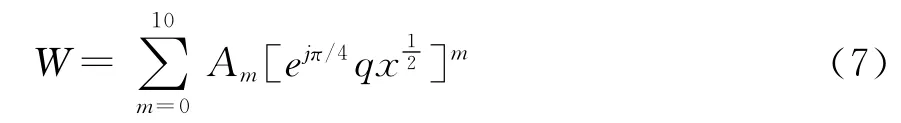
式中，K1为空气中的波数2π／λ（1／km）；λ为真空中的波长（m）；ae为等效地球半径（km）。

3.1 均匀光滑路径上地波衰减函数的计算

当d＜70km时，地面近似为光滑平面地，按照q绝对值大小采用不同的计算公式。

1）｜q｜＞1时，地波衰减函数W的计算公式为：

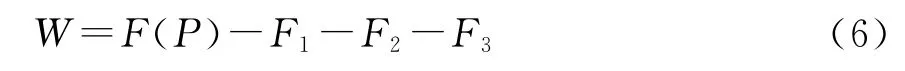
式中，

其中，Am（m＝0，1，…，10）的表达式亦见文献［2］

当收发两点距离d＞70km时，将地面视为光滑球面，地表附近的大气取为标准大气。参数F用Fock的绕射公式来计算：

式中，N是一个足够大的正整数，由级数求和的计算精度而定。由于级数的收敛性，距离越大，级数收敛越快，需要的N越小。这里N无需大于100，就能保证级数的计算精度优于10－6，并可保证与近距离计算结果光滑连续［3］。ts是模方程的第s个复数根。

3.2 分段均匀光滑路径上地波衰减函数的计算

对于分段均匀光滑路径，工程计算上多采用米林顿经验公式。设混合路径可以划分为n段，各段地面距离分别为d1，d2，……，dn，大地电导率分别为σ1，σ2，……，σn，相对介电常数分别为εr1，εr2，εm，则混合路径的地波衰减因子W为：

式中，其中，Δi＝Zi／η为第i段路径上的归一化表面阻抗，Zi为第i段路径上的表面阻抗，η为空气中的波阻抗。W（∑di，Δi）为路径∑di上，电参数为Δi时，按均匀光滑地球的表达式进行计算的地波衰减因子。

3.3 非均匀光滑路径上地波衰减函数的计算

当传播路径是地面电参数和地形特征都有复杂变化的非均匀光滑不规则路径时，地波衰减函数需要用积分方程方法进行数值求解。积分方程法的思路是，首先在均匀光滑路径模型的基础上，仍然近似地认为垂直电偶极子的赫兹矢量只有垂直于地面的分量，同时应用列翁托维奇近似边界条件，借助格林定理和收发天线互阻抗概念，得出实际传播路径主区地波衰减函数的二维积分方程，然后采用稳定相位法将二维积分方程近似地化为一维积分方程，再用迭代法逐步逼近求解［4～5］。

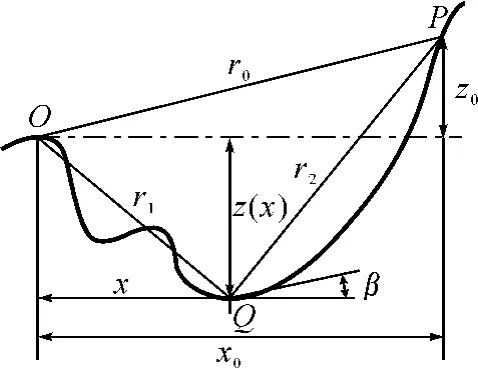
图1 地形剖面和水平投影示意图

非均匀光滑路径的地形剖面示意图如图1所示，在不均匀不光滑的地面上有一垂直电偶极子，场源发射天线在地面上的投影点记为原点O，地面上的接收点记为P，地面上任一积分动点记为Q。

非均匀光滑路径的积分方程推导比较复杂繁琐，在此只给出接收点处于地面时的一维积分公式［6～7］。

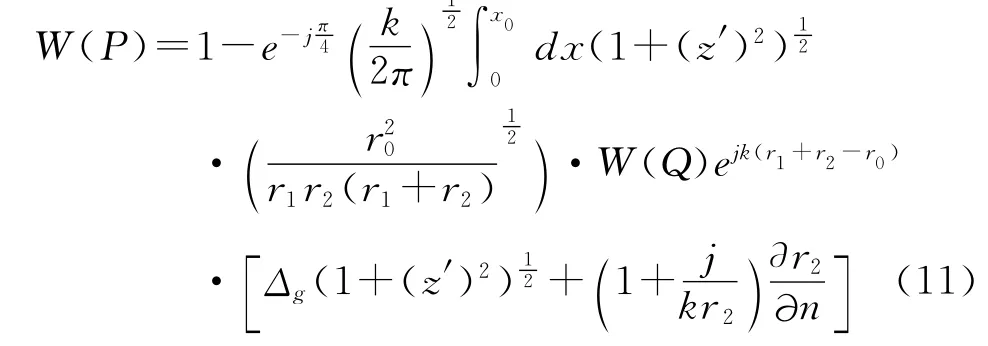
其中，Δg是地面的归一化表面阻抗。z′是地形标高的导数。

4 地波传播ASF的测量

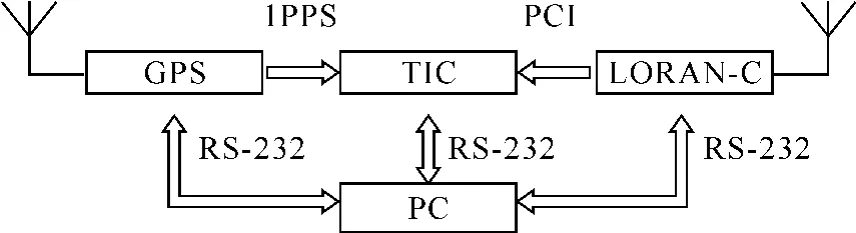
图2 ASF测量框图

ASF测量系统的组成框图如图2所示。用GPS共视法进行时间基准的同步，GPS输出的1pps秒信号作为TIC（时间计数器）的开门信号，罗兰C的PCI信号作为关门信号。ASF的测量框图如图3所示，图中有关参量的含义如下［8］：Master Xmit为主台发射时刻；Station Xmit为副台发射时刻；Emission Delay（ED）为发射延迟，为固定值；Emission Delay Correction（EDC）为发射延迟修正［9］，由罗兰 C 管理机构发布；Master Offset from 1PPS为发射时刻与1PPS之间的偏差；Raw TOA为粗TOA，即接收机测得的伪TOA；Predicted All Seawater Path TOA为接收点到副台之间的路径为全海水路径时的TOAsea，即PF＋SF；Received Delay为接收延迟，可精确测得［10］。由图3，可得到如下关系：

式（13）给出的是副台的ASF表达式。对于主台的ASF，表达式为：

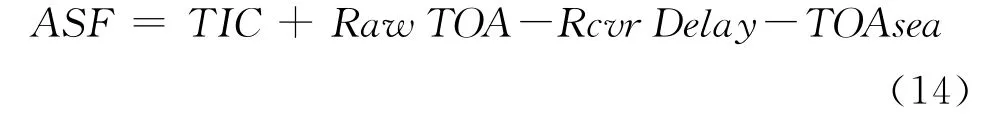
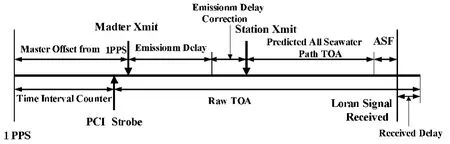
图3 ASF示意图

5 计算及实测结果

表1 传播时延实测值与理论计算值比对

表1给出了部分接收点上，用米林顿法和积分方程法计算出的ASF理论预测值和实测值（单位为微秒）。从表中可以看出，用积分方程法比用米林顿法计算出的ASF值更加符合实测的ASF值，这是因为相比于米林顿法，积分方程法可以有效反映地形对地波传播二次时延的影响。

6 结语

罗兰C信号地波传播的ASF修正有理论预测和实测两种途径。理论预测法需要罗兰C信号覆盖区内的大地电特性数据和大地高程数据以及大气气象数据，但ASF的理论预测精度必须经过实际测量的检验和修正。ASF的测量不可能在广阔的覆盖区内大范围高密度实施，在实际测量ASF时，如何选择测量区域、测量线路和测量密度，在一定程度上又需要理论计算来指导。研究表明，采用理论预测和实测修正相结合的方法，建立罗兰C覆盖区ASF修正数据库是可行的，经ASF修正后的定位精度可得到显著的提高。

［1］海杭.罗兰C使用手册［M］.南京：东南大学出版社，1996：33～34

［2］SJ 20839-2002.长波地波传输信道计算方法［S］.北京：信息产业部，2002：3～6

［3］潘威炎.长波超长波极长波传播［M］.成都：电子科技大学出版社，2004：127～129

［4］熊皓.电磁波传播与空间环境［M］.北京：电子工业出版社，2004：110～117

［5］熊皓.无线电波传播［M］.北京：电子工业出版社，2000：331～363

［6］王东文.不光滑不均匀地面地波传播的积分方程方法［J］.电波与天线，1985（4）：21～35

［7］王东文.复杂地面条件下低频地波传播的三维预测［J］.电波科学学报，1988，3（1）：50～63

［8］Richard H.A Preliminary Study of LORAN-C Additional Secondary Factor（ASF）Variations［R］.Washington，D.C：Proceedings of the 29st Annual ILA Convention and Technical Symposium，2002

［9］宁民，齐鹏辉，李晓强.罗兰C发射台的发射延时测量［J］.导航，2007（1）：43～46

［10］吴海涛.Cs Sync 1000型罗兰C接收机系统时延的测量方法［J］.电子测量与仪器学报，2002，16（3）：22～27