EDA-VNS混合算法在求解同序Flowshop问题中的应用＊-

张 强 王少参 李四超

（海军驻郑州地区军事代表室1） 郑州 450015）（郑州机电工程研究所2） 郑州 450015）

1 前言

自20世纪50年代Johnson发表了第一篇Flow-shop问题论文之后，众多学者开展了关于Flow-shop问题的研究［1］。随着问题规模的不断增大，问题的复杂性呈指数级别增长，传统的分支界定法、构造式启发式算法等精确算法已经无法适应问题规模的增长。与此同时，许多启发式算法诸如遗传算法、蚁群算法和粒子群算法等被应用于Flow-shop问题的求解。

估计分布算法（Estimation Distribution Algorithms，EDA）由 Mühlenbein和 Paaβ［2］提出的，该算法开始于随机产生的种群，通过初始种群的适应度得到一个估计概率。然后，通过该估计分布产生新的个体，这个过程一直重复直至满足结束条件。EDA算法已经被应用于0-1背包问题（Knapsack Problem），旅行商问题（Traveling Salesman Problem）和车间作业调度问题（Job-shop Scheduling Problem）等组合优化问题［3］。

从生物进化角度看，遗传算法模拟了个体之间微观的变化，而分布估计算法则是对生物群体整体分布的建模和模拟［4］。但是，有些较优解群体性表现不强，分布估计算法对这些解搜索不太理想，为了改进EDA的性能，Lozano建议在EDA过程中混合局部搜索算法［6］。本文用 VNS（Variable Neighborhood Search，变邻域结构搜索）算法与EDA结合，来提高EDA算法的性能。

2 用EDA算法求解FSSP

本文提出一种新的概率模型，基于该概率模型对EDA算法进行了改进。下面讨论我们提出的EDA算法在求解FSSP中的应用。

2.1 解的编码和初始解

在诸多文献中，直接用任务序列来表示一个解，本文也采用这样的方式来表示解。为了保证种群中解的广泛性，我们用根据均匀分布来随机产生初始解。

2.2 选择

本文采用的选择策略具体描述如下：

（1）对种群中的每一个个体p，计算其适应度f（p）＝1／TFP（p）；

（2）将每个个体的适应度按升序排列，即适应度高的个体排在前面；

（3）父代的选择基于prob（r）＝2r／p（p＋1），其中r表示个体在已经排列好的适应度集合中的位置。

2.3 概率模型和新个体的产生

概率模型的确定是EDA算法的重要内容，它决定的EDA算法的效果。主要步骤是为父代种群的子集Q建立一个估计分布，在本文的算法中，进行估计分布模型确定的时候既考虑了当前Q中任务在整个任务序列排列又考虑了Q中任务序列的相似性。

假定：

ηjk：在Q被一个参数δ1扩展后，工件j在位置k上或位置k之前出现的次数，ηjk表征了任务序列的重要性。

μj［k－1］：在Q被一个参数δ2扩展后中，工件j在位置k－1之后出现的次数，μj［k－1］表征了任务序列的相似性。我们倾向于保留相似性很大的任务序列。

我们注意到δ1和δ2两个参数是为了增强解的分散性，实际上，这两个参数延缓了算法的收敛速度。

Ωk；到位置k尚未分配位置的工件集合。

我们定义πjk为工件j在k位置的概率，πjk＝ηjk×μj［k－1］／∑l∈Ωk（ηlk×μl［k－1］）。 根 据 这 个 概率，对每一个位置k，我们从尚未分配位置的工件集合Ωk中选择一个工件，直至Ωk为空，产生一个新个体。

2.4 取代

取代是EDA算法中的最后一个步骤，取代的主要操作是更新种群。因此在每一代迭代中，都要根据Q产生子代个体几个O，有许多种方法来确定O中的个体是否被留下。

在我们的算法中，我们用O中的个体与当前种群中最差的个体比较，如果新个体优于当前最差个体，并且新个体的任务序列在种群中是唯一的，此时新个体取代当前种群中的最差个体。

2.5 停止规则

停止条件表示搜索在该条件下终止，有多种停止规则可以使用。例如：最大迭代次数、计算时间限制、若干代没有改进结果等等，我们选用最大迭代次数和计算时间限制来作为停止条件。

3 混合EDA算法求解PFSP

为了提高EDA算法的性能并避免搜索过程陷入局部最优，一个成功的方法就是在EDA算法中加入局部搜索的方法。我们将VNS算法作为一个改善策略与EDA结合用于解决PFSP。

我们在种群的子集Q中应用VNS算法，通过解的质量得到一个改进概率，如果这个改进概率满足条件，就用VNS算法生成一个新的个体。

我们选择两种邻域结构来实现，一种是交换局部搜索，一种是插入局部搜索。第一种邻域结构的构建是通过交换两个不同位置i，j的元素来实现的；第二种邻域结构的构建是通过将i位置的元素插入到j位置之前实现的。（i≠j1≤i，j≤n）设定pc＝exp（－｜RD｜）为应用VNS算法的概率。RD＝（f（xcurrent）－f（xbest））／f（xbest）。对每一个个体，如果pc大于或等于（0，1）之间产生的随机数，我们就用VNS算法产生一个新个体。VNS算法的流程图如图1所示。

4 计算结果

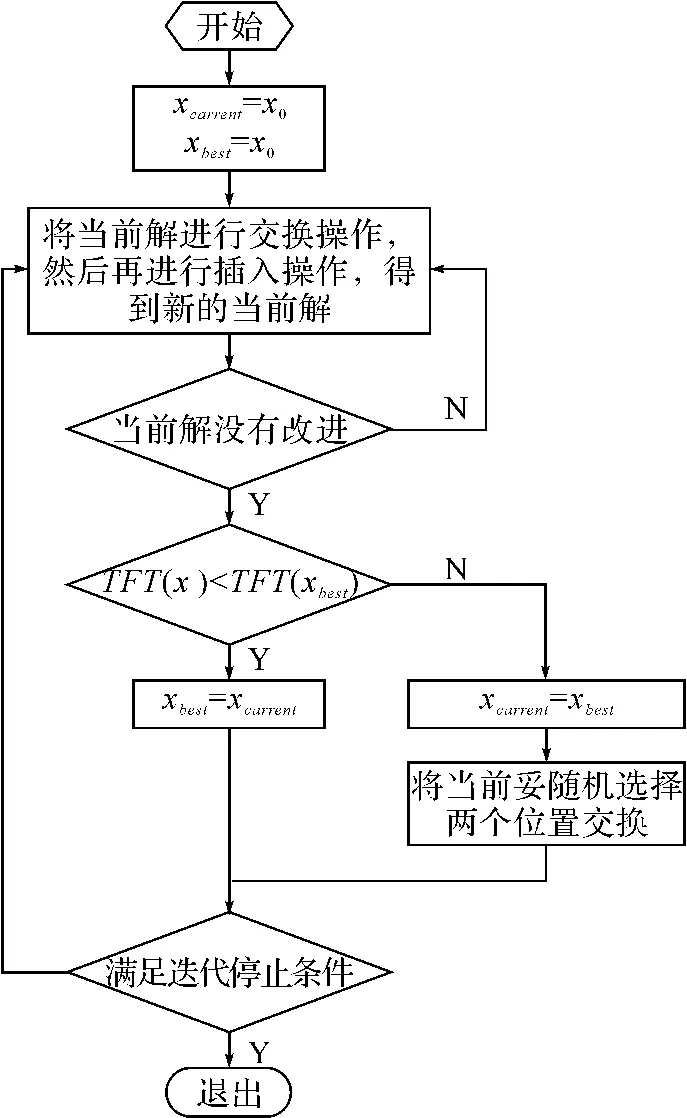
图1 VNS流程图

算法用Visual-Studio2005的c＃进行程序编写，在处理器为2.4G，内存为1G的PC上运行。EDA—VNS混合算法的参数如下：P＝60，δ1＝δ2＝4／n，Q＝O＝3。用 Taillard提出的Flow-shop问题基准实例20×5，20×10和20×20作为算法的求解对象［7］，并将EDA-VNS混合算法和遗传算法的计算结果进行比较。

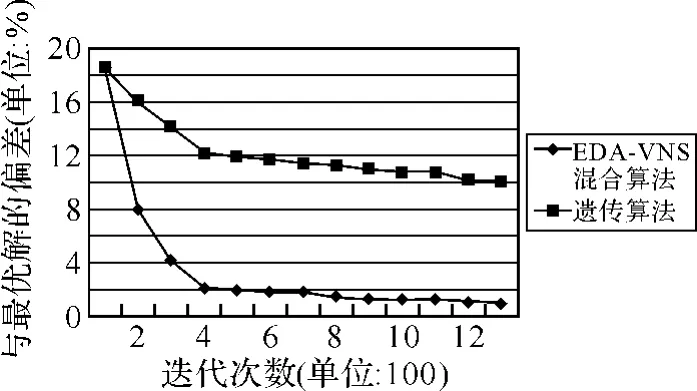
图2 EDA-VNS混合算法和遗传算法计算20×5实例的计算结果

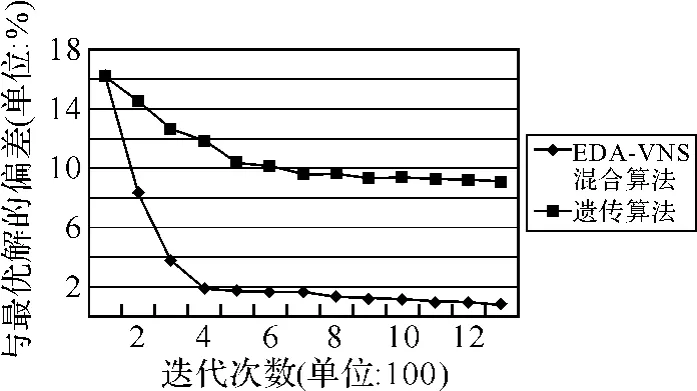
图3 EDA-VNS混合算法和遗传算法计算20×10实例的计算结果

图2，图3和图4是EDA-VNS混合算法和遗传算法分别计算Flow-shop问题基准实例20×5，20×10和20×20的结果对比。从图可以看出，EDA-VNS混合算法在求解Flow-shop问题方面比遗传算法更加有效，在第400代后，EDA-VNS混合算法就得到了质量相当不错的解，而遗传算法在1300代的时候与最优解还有一定的偏差。

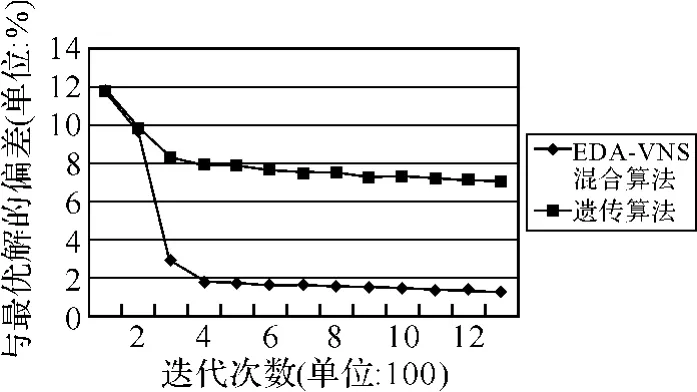
图4 EDA-VNS混合算法和遗传算法计算20×20实例的计算结果

5 结语

本文针对EDA在求解Flow-shop问题时微观概念上的较优解搜索能力不强的缺陷，将VNS算法与EDA集合，配合EDA搜索问题的全局最优。经试验验证，EDA-VNS在求解Flow-shop问题上有良好的性能。

［1］Misuo Gen，Runwei Cheng.Genetic Algorithms and Engineering Design［M］.John Wiley ＆Sons Inc，1997

［2］Mühlenbein H.PaaβG.From recombination of genes to the estimation of distribution.Binary parameters［J］.In：Lecture notes in computer science 1411：parallel problem solving from nature，PPSN，1996 Ⅳ：178～187

［3］Larraanaga，P.，Lozano，J.A.，（Eds）.Estimation of Distribution Algorithms：a new tool for evolutionary computation 2002［M］.Boston／Dordrecht／London：klower Academic publishers，2002

［4］周树德，孙增圻.分布估计算法综述［J］.自动化学报，2007，33（2）：113～124

［5］卢申朋，冯好娣，刘宏.一种有到达时间的多处理器混合流水车间调度的遗传算法（英文）［J］.计算机与数字工程，2008，36（10）

［6］Lozano JA，et al.Towards a New Evolutionary Computer Advances on Estimation of Distribution Algorithms［M］.Berlin：Springer，1996

［7］Taillard E.Benchmarks for basic scheduling problems［J］.European Journal of Operational Research，1993，64：278～285