涡轮弯扭叶片气动设计工程方法研究
赵大勇
(中航工业沈阳发动机设计研究所,沈阳 110015)
涡轮弯扭叶片气动设计工程方法研究
赵大勇
(中航工业沈阳发动机设计研究所,沈阳 110015)
采用弯扭叶片设计是提高燃气涡轮效率的主要手段之一,而构建弯扭叶片积叠线的参数化模式是设计涡轮弯扭叶片的重要基础。为了满足各种涡轮叶片弯扭设计的工程需要,提出了采用圆弧型、抛物线型、分段样条曲线积叠线规律的涡轮弯扭叶片设计方法,编制了积叠线生成代码,并推荐了各方法的应用条件和方式;提出的回归正交设计方法可以对分段样条曲线积叠线的涡轮弯扭叶片进行寻优设计。所提出的弯扭叶片工程设计方法已经在多个涡轮气动设计中得到应用。
弯扭叶片;优化;涡轮;气动设计;积叠线;航空发动机
0 引言
随着航空发动机性能不断提高,对涡轮叶片气动设计要求也越来越高。为了提高涡轮效率,满足总体性能指标,涡轮叶片设计不断采用新技术,包括需要冷却的低压涡轮导叶和动叶,大展弦比的涡轮叶片,具有大扩张角端壁的涡轮导叶等。设计方法经历了初步(1维)设计方法、轴对称通流(2维)设计
方法、求解3维非稳态N-S方程的CFD方法[1]。在涡轮3维气动设计中,根据研究对象不同可细分为单排叶片、单级涡轮和多级涡轮的3维计算分析;根据冷却不同可分为无冷气涡轮流场、加源项方式的有冷气流场和冷却孔分网格考虑冷气的流场分析;进一步引入时间项,可分为稳态流场和非稳态流场分析。
涡轮叶片弯扭设计使叶片3维成型设计迈上了1个新台阶,采用弯扭叶片是提高涡轮效率的主要手段之一。近20年来,弯扭叶片设计已经被广泛研究[2-3],在国内外多型航空发动机上得到应用,如湍达系列发动机等[4]。构建弯扭叶片积叠线是涡轮弯扭叶片设计的重要基础。目前国内弯扭叶片设计中,设计师一般根据经验设计积叠线形式。由于积叠线空间解范围很大,所以设计结果随机性很大,所得设计解是否为最优解或较优解很难评判;而且需要花费大量时间。涡轮弯扭叶片研究公开发表的论文多采用标准叶型(如NACA65叶型)进行机理性研究,没有构建叶片积叠线的参数化程序,设计结果受设计工程师经验和人工因素的影响较大,而且积叠线的构建形式也相对单一,限定了叶片的可能形式,对其后叶片优化设计工作有较大影响。在弯扭叶片设计中对采用的叶片积叠线设计方法进行总结,编制程序代码,定义积叠方式,并界定各种方法的适用情况和方法,对消除设计师人工随机性影响尤为重要,而且可以提高效率,缩短设计周期,对设计解的覆盖面有保障,大幅提高获得较优解的几率,达到提高涡轮工作效率的目的。
1 涡轮弯扭叶片积叠线参数化设计方法
某一涡轮叶栅出口能量损失典型分布如图1所示。根据低压涡轮导叶出口能量损失分布规律,叶栅损失区域可以分为3部分:中部低损失区和根、尖逐渐增大的高损失区。叶栅中部主要是叶型的摩擦损失,靠近端壁为摩擦损失和2次流损失的叠加。
叶片弯扭设计的作用主要是降低端壁附近区域的2次流损失区[2]。为了降低端壁附近区域2次流损失,同时考虑结构装配的工程问题,提出了分段样条曲线、圆弧型、抛物线型积叠线规律的涡轮弯扭叶片设计方法。
1.1 分段样条曲线积叠线设计方法
分段样条曲线积叠线如图2所示。从图中可见,积叠线共分为5段,包括3个直线段和2个3次样条曲线段。图中,D、XH、XT、BH、BM、BT为用叶片高度进行无量纲处理后的值:D为相对叶根基准叶尖沿切线方向的偏移量,或中部为径向的开关;XH、XT分别为根部和尖部直线段所占高度;BH、BM、BT分别为各部分直线段所占高度;AH、AT分别为叶根和叶尖的倾斜角度。

有时希望生成的积叠线的中部直线段方向保持为径向,为了节省自变量个数,用D来实现。当D取值为1.5时(叶尖偏移量为1.5倍的叶高,选择1个不具备工程设计意义的数值),D值只代表计算开关,生成的积叠线将保持中部直线段为径向。
采用该方法可以生成如图3所示的各种积叠线,包括不同程度的正弯、反弯,以及J、S型的弯曲规律。倾斜直线、3次样条等方式也可以作为本方法的1个特例。

1.2 圆弧型积叠线设计方法
叶片弯扭设计增加了冷却叶片结构的设计难度,因为其必须考虑结构通气导管装配问题,而影响导管安装的不仅是叶片根部、尖部倾角的具体数值,还包括叶片沿径向的弯曲规律分布。为此,本文提出了圆弧型积叠线设计思想。
涡轮叶片圆弧型积叠线可以通过求解2次曲线方程得到。求解2次曲线方程需要3个约束条件,首先是定义叶片根部为坐标圆点,再附加2个约束条件,沿用设计人员的使用习惯,选择根部和尖部倾角。进行导叶积叠设计时按照最大厚度积叠,再附加圆弧型积叠规律,可以降低冷却叶片结构设计难度。采用圆弧型规律生成的1族积叠线如图4所示。该圆弧型积叠线设计,成功解决了在某型发动机低压涡轮冷却叶片设计中遇到的通气导管装配问题,还成功应用于某小型燃气轮机高压涡轮导叶设计中。
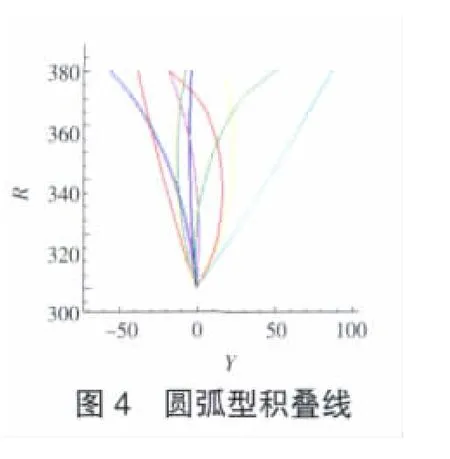
1.3 改进的抛物线型积叠线设计方法

抛物线型积叠线控制参数少,易于实现优化,但不能用于设计S型叶片,对叶片内导管安装也不是很有利。采用抛物线型规律生成的1族积叠线如图5所示。为了弥补该缺陷,用分段直线和样条方法相结合的积叠方式设计与抛物线型类似的叶片。采用该方法的优点是自变量数量少,但可能会丢失最优解,可在实心叶片初步设计时使用,然后再用分段方法寻优。
2 叶片积叠线规律寻优方法
目前没有通用的经验公式和方法可以直接得到与叶型相匹配的积叠规律。对于工程设计任务,时间节点的限制是重要的约束条件,如何在有限时间内快速得到最优积叠规律是弯扭叶片设计的重点和难点。
2.1 圆弧型和抛物线型积叠线寻优方法
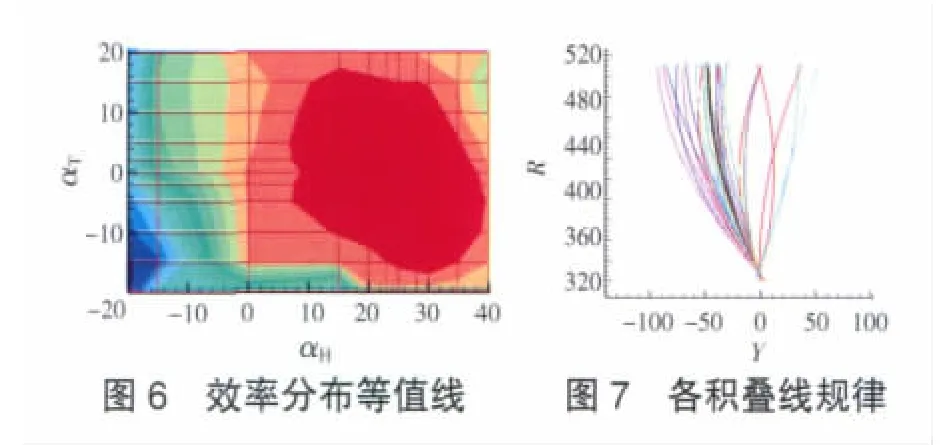
采用圆弧型和抛物线方法设计弯扭叶片,因为自变量只有2个,可以采用黄金分割法[5]或精化网格法实施优化。经过多个算例的计算,相邻算例的目标函数差小于程序的计算精度时,寻优过程结束,可以得到1个等值线图。优化过程示例见表1。表中各行、列分别表示积叠线根部、尖部倾斜角度。依据表1数据绘制的效率等值线如图6所示。图中横、纵坐标分别表示积叠线根部、尖部倾斜角度(αH和αT)。各计算点积叠线分布规律如图7所示,图中黑线对应表1和图6中的效率取得最高值的积叠规律。圆弧型和抛物线型积叠线的叶片3维示意图如图8所示。
2.2 分段样条曲线积叠线寻优方法
分段样条曲线方法的自变量数目较多,包含8个独立变化的自变量,计算域空间较大,在有限时间内快速寻优是1个难点,可采用回归正交设计方法寻优[6-7]。

正交表是根据组合理论按照一定规律构造的表格,在试验设计中应用广泛。以正交表为工具安排试验方案和进行结果分析的试验称为正交试验,适用于多因素、多指标、多因素间存在交互作用、具有随机误差的试验。通过正交试验,可以分析各因素及其交互作用对试验指标的影响,按其重要程度找出主次关系,并确定对试验指标的最优工艺条件[7]。
在弯扭叶片设计中,积叠规律受叶片叶型、子午流道形状和工作条件等多方面的影响,目前尚不能用解析方法求解。叶片积叠线按照上述参数化表示以后,其解的空间仍然较大,且各参数之间存在较强的相互影响。考虑到受加工水平和流场计算水平的影响,设定叶片优化过程结束的衡量标准为相近计算结果的误差小于精度目标。上述特征决定了宜采用正交设计方法。根据叶片积叠线参数化的方法,选择L18(2×37)正交表(见表2)设计比较适宜。

表1 精化网格法(抛物线积叠线)初步优化示例
表2中8列数字表示积叠线参数化后的自变量,分别表示 D、AH、AT、XH、XT、BH、BM、BT参数;18行数字代表1轮试验(计算)次数。根据数理统计方法确定数值试验指标之分项和、指标均值和极差,从而评定各项参数对级效率影响的重要程度,依照各项参数指标值的极差大小排出重要性顺序,推论出最优参数组合方案作为下一轮寻优的基准。
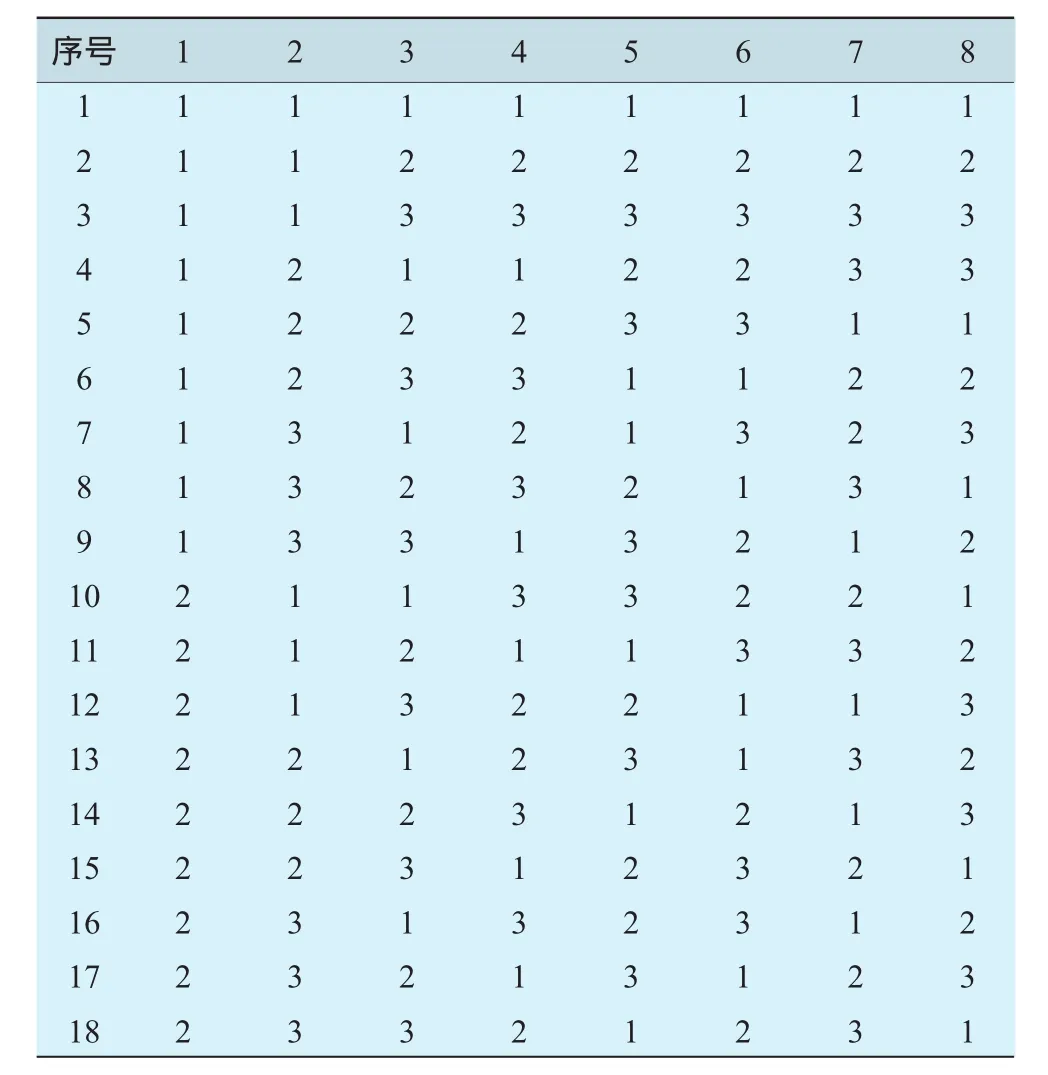
表2 L18(2×37)正交表
在前述抛物线优化的基础上,合理选择分段样条曲线积叠线参数,见表3。按照表3取值,得到18个需要计算(数值试验)的方案,如图9所示。对各方案分别进行3维流场计算,得到涡轮级效率计算结果,见表4。带有分段样条曲线积叠线涡轮导叶的涡轮级(3维)如图10所示。
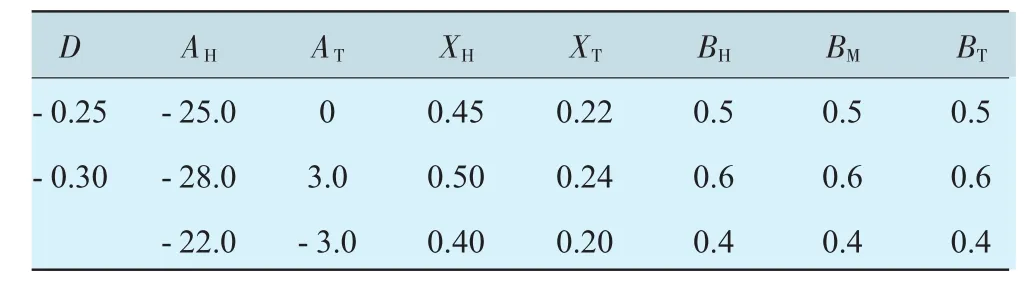
表3 积叠线参数优化设计取值
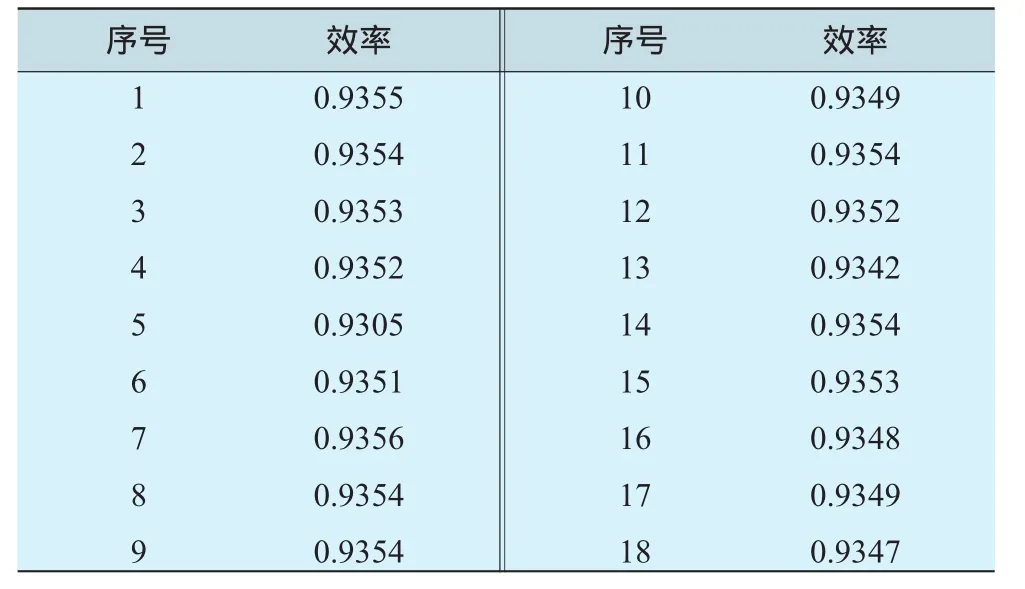
表4 流场分析计算结果
对表4中数据进行分析,结果见表5。从表5中可见,对效率影响最大的几何参数为XT(即尖部直线段部分所占高度的比例),其它影响较大的参 数 还 有 XH、AH、BT,而参数D的影响最小。
根据正交设计方法和计算结果可以确定下一轮优化推荐基准取值,见表6。
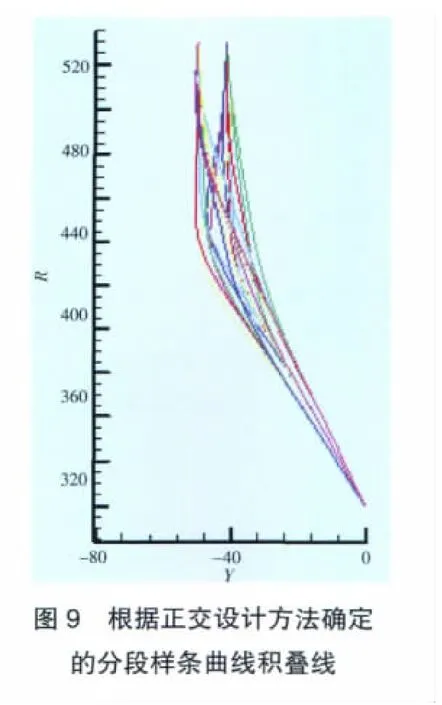


表5 积叠线参数重要性分析

表6 经过1轮优化计算后的推荐基准取值
经过多轮次寻优计算,可以改善叶片积叠线与叶片基元型线的匹配关系,达到提高涡轮级效率的目的。该方法还可以应用于掠形叶片设计。
3 积叠线曲线生成程序
为便于工程设计应用,采用上述方法编写了积叠线曲线生成代码。为保证程序使用范围,积叠线生成程序保留了传统的抛物线积叠方法,作为2次曲线,自变量选择叶片根部和尖部的倾角。代码中也包含了积叠线生成程序与叶片造型程序、涡轮流场3维计算软件的接口程序,同时也包含了正交回归优化过程的数据处理程序。结合积叠线生成程序、叶片设计软件和涡轮流场3维计算软件,目前已用于多型涡轮导叶设计中。
4 从寻优解中选择最终方案

通过对空间内多个方案进行寻优分析,可以在众多方案中锁定可供选择的几个方案。而如何选择最终方案,需要综合考虑目标函数的计算结果和设计对象的具体设计要求。比如,在如图11所示的设计结果曲线中,按照数学优化方法,设计结果将选择A点,如果设计要求为A1,由于B点没有达到,则A点是1个合适的设计结果;但是如果设计要求为B1,那么选择A点将存在不足,因为A点右侧曲线段目标值衰减过快,假设累计误差符合正态分布,且在选择A或B点情况下误差分布相同,与A点相比,选择B点将提高产品合格率,所以最终方案应该选择B点。也就是说,受多种因素影响的设计方案,需要参考计算结果分布曲线,并综合考虑各方面影响做出选择。
在涡轮弯扭叶片设计中,无论采用何种积叠线形式和优化方式,都需要根据参数化和优化的具体情况,综合考虑气动、结构、强度等方面的具体要求,做出合理选择。
5 结论
(1)采用圆弧型、抛物线型、分段样条曲线积叠线规律的涡轮弯扭叶片设计方法,可以用于设计有特定要求的弯扭叶片,不仅可以提高涡轮效率,还可以解决工程设计中存在的一些实际问题;
(2)采用回归正交设计方法对分段样条曲线积叠线的涡轮弯扭叶片进行优化设计,可以有效提高弯扭叶片设计水平,贴近最优解;
(3)根据本文所述方法编写的积叠线曲线生成代码,可以自动生成圆弧型、抛物线型、分段样条曲线积叠线,减少了设计工具的人工因素影响,缩短了设计周期,有效提高了设计效率,可满足工程设计需要。
[1]Shahrokh Shahpar.Three-dimensional design and optimisation of turbomachinery blades using the Navier-Stokes equations[R].ISABE-2001-1053.
[2]王仲奇.采用弯扭静叶片的燃气透平设计计算方法[R].CSAA-90-PT-12.
[3]Chen N X.An exhaustive studyon skewingeffect ofsabre-shape blades in a turbine stator[R].ISABE-95-7055.
[4]陈光.“湍达”发动机设计特点[J].国际航空,1991(3):40-41.
[5]陈立周,周培德,高云章.机械优化设计方法[M].北京:冶金工业出版社,1985:50-52.
[6]朱伟勇,关颖男.最优设计理论与应用[M].沈阳:辽宁人民出版社,1981:146-249.
[7]数学手册编写组.数学手册[M].北京:人民教育出版社,1979:809-859.
Aerodynamic Design Engineering Method of Bending-torsion Turbine Blade
ZHAO Da-yong
(AVIC Shengyang Aeroengine Research Institute,Shenyang 110015,China)
Bending-torsion blade is one of the main methods to improve turbine efficiency,construction of bending-torsion stacking line parametric mode is the important base for design of the turbine bending-torsion blade.To meet the engineering requirement of various turbine bending-torsion blade,the design method about arc,parabola,subsection spline curve stacking line rules were introduced,stacking line generating code was complied,and the application conditions and methods were suggested.The regression orthogonality design method can optimize the design of turbine bending-torsion blade with subsection spline curve stacking line.The bending-torsion balde engineering design method has been used in several turbine aerodynamic design.
bending-torsion blade;optimization;turbine;aerodynamic design;stacking line;aeroengine

赵大勇(1970),男,高级工程师,从事涡轮性能设计工作。

