飞机牵引车自动转向控制

王能建，周丽杰

(哈尔滨工程大学机电学院，黑龙江哈尔滨150001)

飞机在地面上的移动主要依靠飞机牵引车.无杆牵引车作为机场地面保障的一项前沿技术已经被广泛使用，其通过自身的夹持装置与飞机前起落架相连，使飞机的部分重量转移为牵引车的附着重量，因此与传统有杆牵引车相比，显著提高了飞机牵引的操纵稳定性、灵活性［1-2］.牵引车一般工作在机场、甲板等狭窄的场地上，为了避免与其他飞机或设备相撞，要求所牵引的飞机有很好的轨迹跟踪性能.另外从操纵性能的角度出发，由于飞机的质量和体积较大且价格昂贵，要求飞机在地面行驶时有一定的稳定性.目前无杆牵引车的操纵主要依靠有经验的驾驶员，但随着近几年飞机的种类和数量不断增多，牵引车的工作越来越繁忙，这就对飞机牵引的快速性和安全性提出了更高的要求.

在过去十多年中发展起来的自动转向技术引起了各国学者的关注，主要将其应用与各种铰接列车，如高速公路上的汽车列车［3］、农业上用的牵引车［4］以及韩国的双峰有轨电车［5］、澳大利亚的多节铰接列车［5］等.自动转向技术的主要优点是减轻驾驶员疲劳，降低运输成本，保证铰接车辆的行驶安全性如:使牵引车及列车精确地跟踪指定轨迹，并保持很好的操纵稳定性.为了实现侧向的轨迹跟踪，首先需采用GPS、视觉导航、光学侧标-激光雷达导航等技术测量汽车的侧向跟踪误差;再基于所建立的系统模型设计牵引车及列车的自动转角控制器.其中基于线性模型已经设计出鲁棒控制器、线性参数变化控制器和二次最优控制器，基于非线性及不确定模型设计出了精确线性化控制器、自适应控制器和滑膜控制器等［6-7］.为了实现稳定性的控制，基于极点配置、鲁棒反馈和变结构等原理设计了列车后轮转角控制器.

将自动转向控制技术应用于具有铰接结构的飞机牵引系统，可以很好地满足牵引车的操纵需求.针对飞机牵引系统的特点:行驶速度较低，牵引车和飞机之间会产生大的铰接角，且不能被忽略;同种型号的牵引车需要牵引不同结构参数的飞机.本文采用牛顿-欧拉方法建立了包含牵引车转向子系统在内的牵引系统非线性动力学模型.考虑到飞机结构参数的不确定性和牵引系统运行转态的多变性，采用反演变结构控制方法，设计出具有鲁棒性能的牵引车前、后轮转角自动转向控制器，使得牵引系统具有很好的轨迹跟踪性能和稳定性.

1 飞机牵引系统动力学模型

图1为无杆飞机牵引系统力学模型.其中，y1，ε1为牵引车的侧向位移和横摆角;Iz1，Iz2为牵引车和飞机的转动惯量;l1，l2为牵引车前后轴到质心的距离;l3，l4为飞机前后轴到质心的距离;l5为牵引车质心到铰接点的距离.Fy1，Fy2，Fy3为牵引车前后轮和飞机主起落架轮胎的侧向力;εf为飞机相对于牵引车的横摆角.

牵引车工作时将飞机的前起落架背负起来，使其离开地面，此时飞机只有主轮与地面接触，牵引车和飞机之间存在一个铰接点.

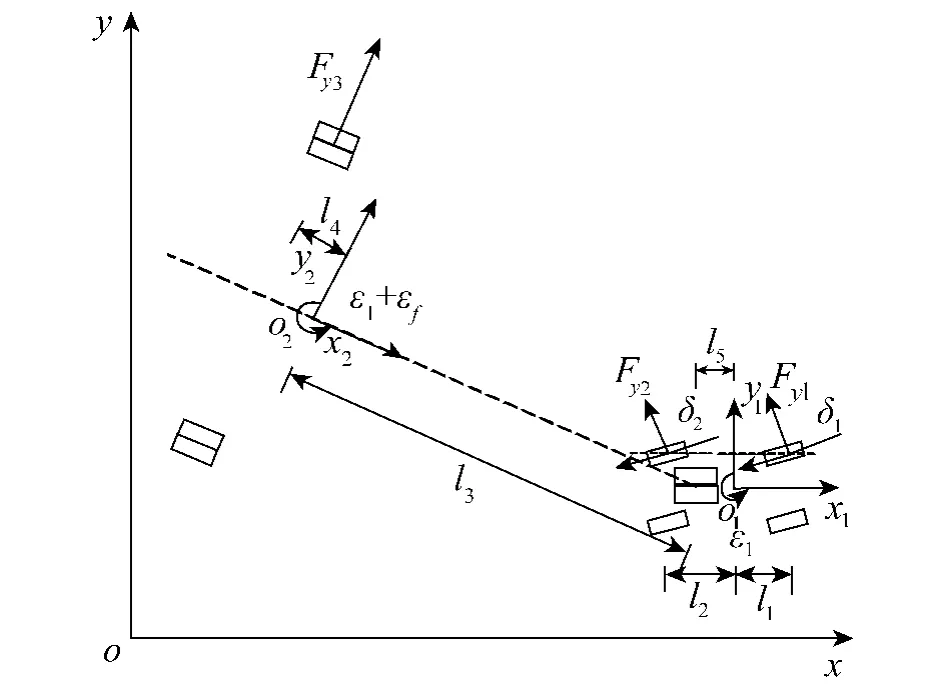
图1 系统动力学模型Fig.1 System dynamic model

1.1 牵引系统模型

对于低速行驶的飞机牵引系统，当转弯半径小时，必须考虑铰接角引起的非线性因素［8-9］.

根据牛顿-欧拉定理对牵引车和飞机分别建立横向和横摆运动的微分方程:

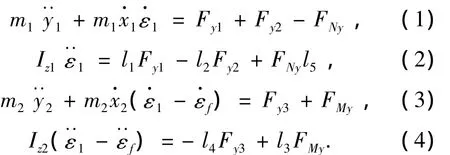
式中:m1、m2为牵引车和飞机的质量;FNy、FMy为铰接点处牵引车和飞机所受的侧向力.

牵引车和飞机铰接点处的作用力的关系为

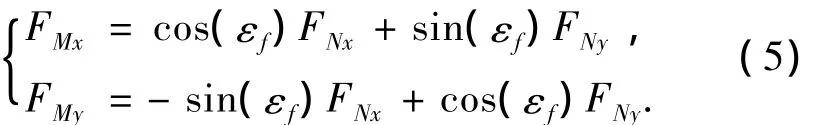
铰接点处的速度及加速度的约束方程为

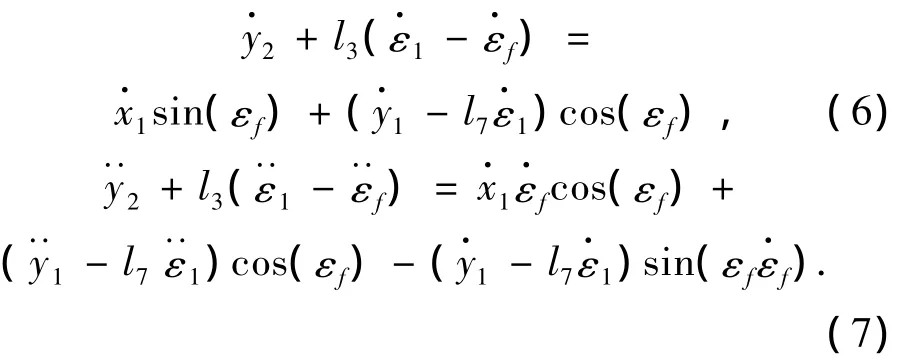
牵引车牵引飞机时行驶速度低，轮胎特性近似为线性:

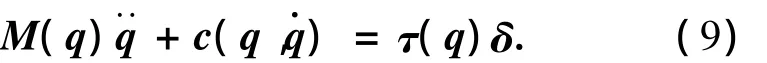
其中，q=［y1ε1εf］T;δ =［δfδr］T;M(q)是 3 ×3 的矩阵 M(q)=［Mij］，(i，j=1，2，3);τ(q)为 3 ×2 矩阵 τ(q)=［τij］，(i=1，2，3;j=1，2).

1.2 轨迹参考坐标系

牵引车自动转向的主要目的是使飞机的前起落架能够很好地跟踪指定的轨迹.对于无杆牵引车，飞机的前起落架背负在牵引车上，其行驶轨迹与牵引车此时的质心位置是相近的，因此保证牵引车质心跟踪指定轨迹即可.为了量化牵引车的侧向跟踪误差，建立轨迹参考坐标系［10］如图2所示.

图中xr轴与轨迹曲线相切，yr轴经过牵引车的质心，εd为轨迹的曲率半径.牵引车连体坐标系与轨迹参考坐标系的转换关系为

式中:c1、c2为牵引车前后轮胎的侧偏刚度;c3为飞机主起落架轮胎的侧偏刚度;δf、δr为牵引车前、后轮转角.

利用铰接点处的相互作用力消去非独立变量，即可将上述三自由度非线性动力学方程整理成矩阵形式:

式中:εr为牵引车相对轨迹坐标系的横摆角速.

图2 牵引车坐标系和轨迹坐标系Fig.2 Tractor and trajectory coordinate system

只要路面参考坐标系确定，就可以根据状态变量的转换关系在轨迹参考坐标系中表达飞机牵引系统模型，方程的矩阵形式为

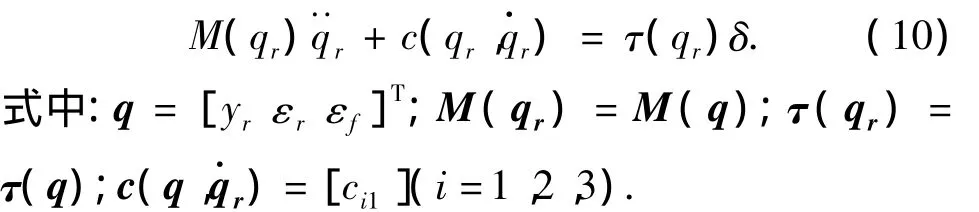
1.3 输入-输出解偶

确定飞机牵引系统的2个控制目标:牵引车相对轨迹的侧偏位移yr和牵引车与飞机之间的相对横摆角εf，则系统控制输出为

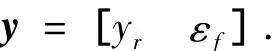
对方程(12)进行解偶得

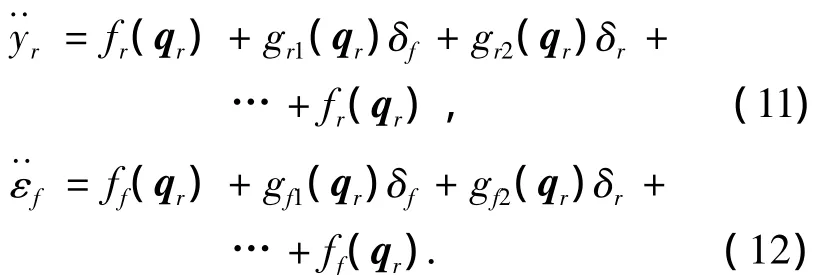
式中:fr(qr)、ff(qr)为未建模动态和时变参数引起的不确定性，主要由不确定参数 l3、l4、Iz2、m2、Iz1、m1、l1、l2、l5、c3(飞机将自身的部分质量转移到牵引车上，导致牵引车的参数也发生改变)和不确定行驶参数u组成.

采用Backstepping变结构控制方法设计飞机牵引系统的控制器，不确定系统可以不满足传统变结构控制要求的匹配条件，控制器对系统的不确定性fr(qr)、ff(qr)是不变的［11］.

1.4 转向系统动力学

转向系统作为牵引车的重要组成部分，在牵引车的侧向控制设计中是不能够被忽略的.一般转向系统的阻尼和刚度都远大于转向系统的转动惯量，忽略转动惯量，转向系统可以表达为二阶系统［12］:

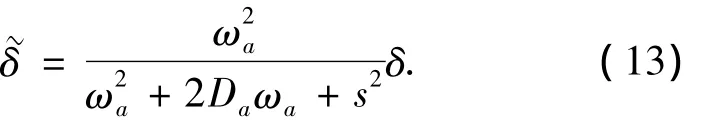
式中:δ为转向轮实际的转角输入，Da为阻尼比，ωa为无阻尼自然频率.

2 Backstepping变结构控制器设计

2.1 控制器设计

综合式(11)、(12)得到系统状态方程的标准形式:

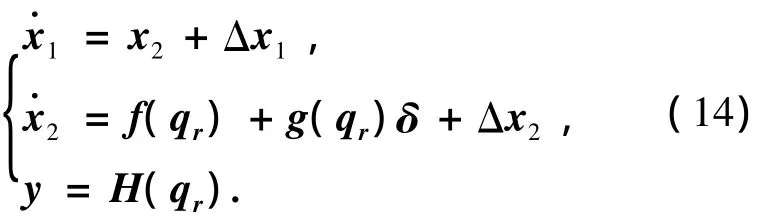
假设存在光滑函数 αi(x1，…，xi)，i=1，2，使得

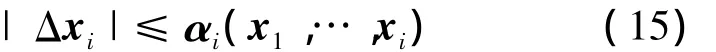
取xi(i=1，2)为虚拟控制，其期望值为 xid，则定义控制误差为

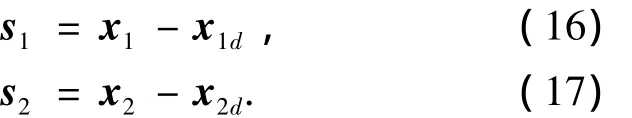
1)对s1求导

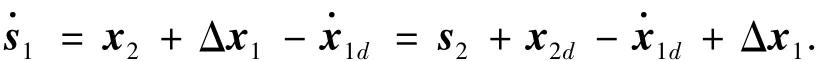
定义Lyapunov函数，并对其求导得

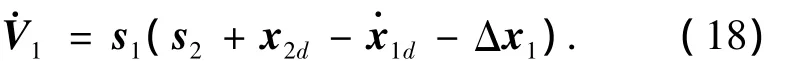
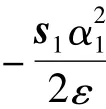
2)对s2求导:

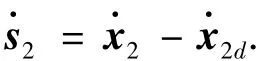
其中，x2d是x1的函数，因此x·2d可分为确定和不确定项，记为∇x2d和Δx·2d，则得到

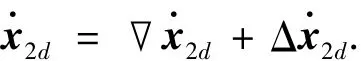
根据假设(15)，能找到光滑函数β2(x1)，使得

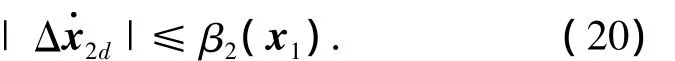
得s2导数为

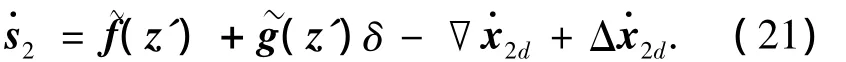
定义Lyapunov函数:

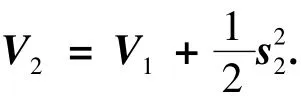
结合式(19)、(21)得

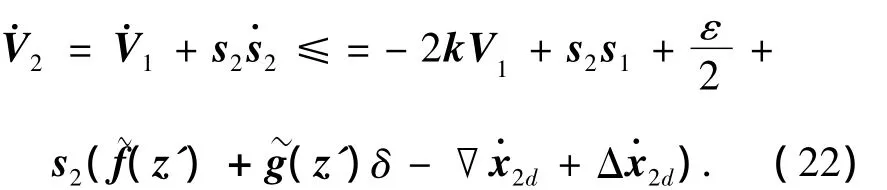
针对式(22)选择变结构控制律为

对非线性系统式(14)选择控制律(22)可以保证 yr，εf对期望信号 yrd，εfd是有界跟踪的，跟踪误差小于(ε/2k)1/2.

2.2 抖振现象消弱

变结构控制系统最突出的问题就是其抖振现象.为了消除这种现象引入边界层法，即用sat(s/Δ)代替 sgn(s)，其中

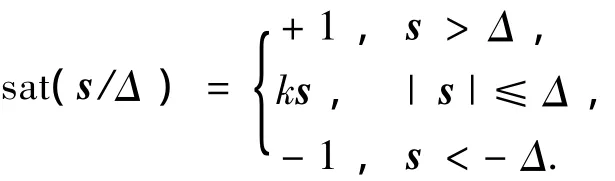
式中:Δ为边界层厚度

3 仿真结果和分析

以某型号牵引车和飞机为例，在simulink上建立上述系统的仿真模型如图3所示.

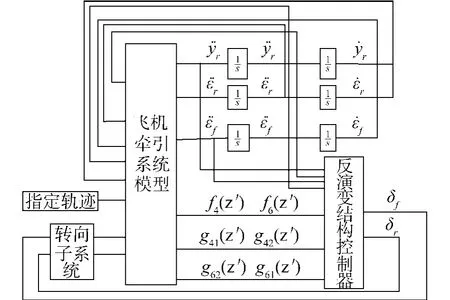
图3 Backstepping变结构控制仿真模型Fig.3 Simulation model with backstepping variable structure control

假设牵引系统行驶的指定轨迹如图4所示，系统初始轨迹偏差为 0.1 m.牵引车牵引飞机以20 km/h向前行驶.

实验1 采用Backstepping变结构控制方法，只对牵引车前轮施加控制使偏移距离趋向0.

实验2 当牵引系统相对横摆角Ra的绝对值小于0.04 rad时，只对牵引车前轮施加转向控制，当相对横摆角的绝对值大于0.04 rad时，添加后轮转向控制，使其值小于等于0.04 rad.对上述两种情况进行对比，仿真结果如图5、6所示.由图5可以看出两种控制方式都能使牵引系统很好的跟踪指定的轨迹，牵引车质心的侧偏位移Ld近似为0.在图6中，出现相对横摆角为-0.06 rad的情况时，实验2中的后轮转向使其值迅速恢复到-0.04，使牵引系统的运动变得更加平稳.

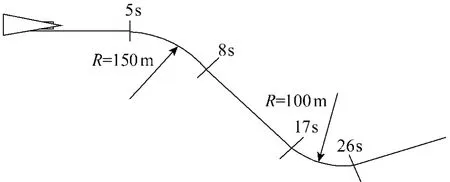
图4 仿真轨迹Fig.4 Simulation scenario

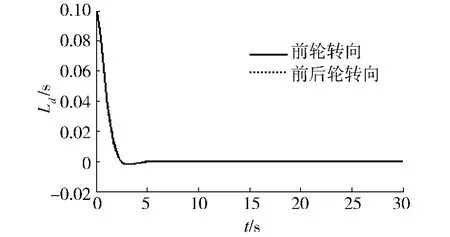
图5 偏移距离Fig.5 Lateral displace ment

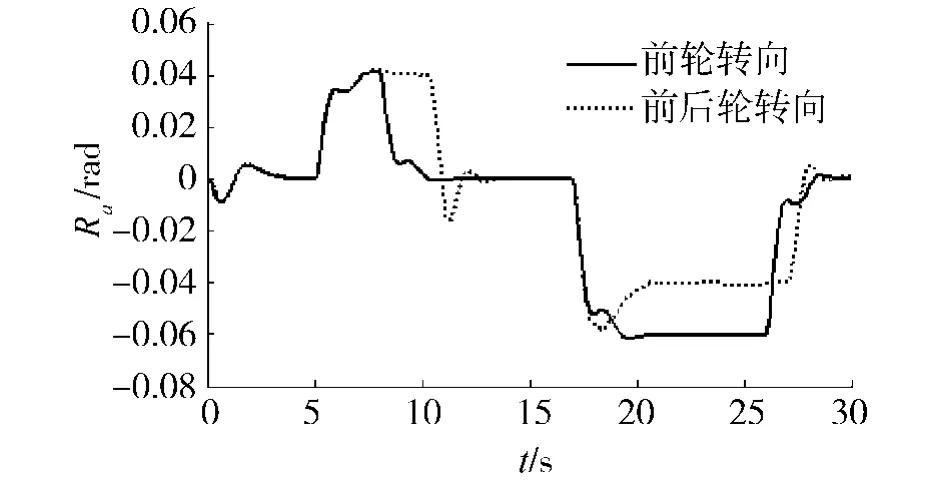
图6 相对横摆角Fig.6 Relative angle

实验3 仿真的初始条件与上相同，采用实验2的转向方式，分别选择3种型号的飞机m1、m2、m3，(其质量分别为:m1=54 975 kg，m2=78 536 kg，m3=94 243 kg)轮胎侧偏刚度和结构参数也随飞机型号的不同而不同进行仿真实验，仿真结果如图7、8所示.由图7得到当牵引不同型号的飞机时，变结构控制器都可以使系统很好的跟随期望的轨迹，从而保证了控制的鲁棒性.图8表明，牵引质量为m1的飞机时横摆角小于0.04 rad，后轮没有参与转向，牵引质量为m2、m3的飞机时，一旦相对横摆角的绝对值大于0.04 rad时，后轮转角就起到了增强稳定性的作用.

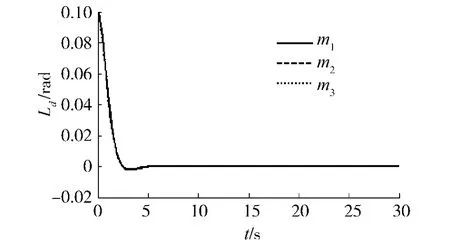
图7 牵引不同飞机时的偏移距离Fig.7 Lateral displace by towing variable type aircrafts

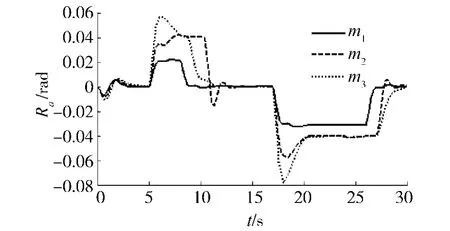
图8 牵引不同型号飞机时的相对横摆角Fig.8 Relative angle by towing various types of aircrafts

4 结束语

针对无杆飞机牵引系统行驶的特殊性，本文考虑铰接角的影响，建立了无杆飞机牵引系统非线性动力学模型.基于输入输出解偶方法，采用Backstepping变结构方法设计了系统转向控制器.仿真结果表明，与只对前轮施加转向控制相比，对牵引车后轮施加控制不仅可以使系统很好地追踪指定轨迹，且可以实现对系统稳定性的控制，避免了折叠现象的产生.当牵引不同型号的飞机时，系统仍能实现控制目标，具有很好的鲁棒性.

［1］FRANCKE E，MOLZER P.Turnout protection for aircraft tractor，United Stated:US 005516252A［P］.1996.

［2］毛小馨，刘贵明.基于SolidWorks的无杆飞机牵引车驱动桥结构设计仿真分析［J］.机械设计，2010:27(2):67-69.

MAO Xiaoxin，LIU Guiming.Structural design and simulative analysis on drive axle of rod-less airplane tractor based on SolidWorks［J］.Journal of Machine Design，2010:27(2):67-69.

［3］CHEN C，TOMIZUKA M.Lateral control of tractor-semitrailer vehicles in automated highway systems［R］.Berkeley:University of California，1996.

［4］DERRICK J B，BEVLY D M.Adaptive control of a farm tractor with varying yaw dynamics accounting for actuator dynamics and saturations［C］//17th IEEE International Conference on Control Applications Part of 2008 IEEE Multiconference on Systems and Control.San Antonlo，Texas，USA，2008.

［5］KIM Y C，MIN K D，YUN K H，et al.Steering control for lateral guidance of an all wheel steered vehicle［C］//International Conference on Control，Automation and Systems.COEX，Seoul，Korea，2008.

［6］毛延娥，井元伟，张嗣瀛，等.汽车ABS滑模变结构控制方法的研究［J］.系统仿真学报，2008:20(5):1243-1245.

MAO Yane，JING Yuanwei，ZHANG Siying，et al.On variable structure control with sliding mode for automotive antilock braking systems［J］.Journal of System Simulation，2008:20(5):1243-1245.

［7］任殿波，张京明，张继业.具有不确定参数的车辆跟随滑模控制［J］.电机与控制学报，2010，14(1):73-77.

REN Dianbo，ZHANG Jingming，ZHANG Jiye.Sliding mode control for vehicle following with parametric uncertainty［J］.Electric Machines and Control，2010，14(1):73-77.

［8］FLETCHER C，MANZIE C，GOOD M.Trailer steering:an Australian rresearch perspective and application for by-wire control［R］.California:University of Melbourne，2004.

［9］CHEN C，TOMIZUKA M.Modeling and control of articulated vehicles［R］.Berkeley:University of California，1997.

［10］胡跃明.变结构控制理论与应用［M］.北京:科学出版社，2003:39-63.

HU Yueming.Theory and application on variable structure control［M］.Beijing:Science Press，2003:39-63.

［11］HINGWE P，WANG J Y，TAI M，et al.Lateral control of heavy vehicles for automated systems:final report for MOU 313［R］.Berkeley:University of California，2003.

［12］HECKER S.Robust H∞-based vehicle steering control design［C］//International Conference on Control Applications.Munich，Germany，2006.