遗传算法研究和探讨

范文广

（安徽国防科技职业学院,安徽六安 237011）

遗传算法（Genetic Algorithm又称GA）是借鉴生物遗传学和自然选择机理的一类优化搜索算法。它不同于传统的数学模型,主要适用于非线性等复杂问题的解决,同时通过进化计算和遗传算法操作,使种群达到优化状态。

1 遗传算法的特点

遗传算法[1]是通过选择、遗传、变异等操作及适者生存的理论,利用简单的编码技术和繁殖机制来描述较复杂的现象,以达到解决非常困难问题的目的,能从多极值、离散的、含噪音的多维问题中搜索到最优解,非常适用于规模较大的并行计算。目前广泛应用在机器学习、并行处理等领域。但它并不能确保问题的答案是最佳的,只是将误差控制在一定的范围内。

遗传算法不是针对参数本身进行进化,而是对参数形成数据集合的编码,将问题结构变换为有限字符串形成编码,然后模仿生物遗传对其进化处理,减少约束条件的限制,优化了计算。

遗传算法具有并行性,它组织搜索是从问题解的种群开始并可以同时向不同的方向,不是从单个解开始。因而可以对多个区域进行搜索,避免了陷入局部最优解而无法跳出的局面。

遗传算法的搜索由问题的适应度函数来指导,不需要外部的辅助信息,不象其它方法需要类似导数值等辅助信息,从而有效地提高了搜索效率。

遗传算法采用了选择、交叉和变异等操作而不是用确定性规则进行随机操作,使搜索过程更具有灵活性和鲁棒性。

2 基本遗传算法

遗传算法类似于生物进化,是通过搜索基因上的染色体来求解,它和需要解的问题本身没有任何关联,只是评价算法所产生的每个染色体,并通过适应值来对染色体进行筛选,选择适应性好的染色体,以便继续繁殖。在遗传算法中,染色体的形成是通过所求解问题的编码随机获取,得到初始种群。对每个个体用适应度函数进行评价,对适应值低的个体淘汰,适应值高的个体参加遗传操作,从而形成下一代新种群,再对新种群进行进化,这样反复操作,最后可得到最优解。

3 遗传算法的基本操作

3.1 编码方案

对于具有复杂结构的应用性问题,为了能够对其进行描述,往往用简单的位串编码来表示。这种用位串形式编码表示问题结构的变换方式称之为编码或编码方案[2],该编码表示称为染色体或称为个体。编码是建立遗传算法的基础,它影响着算法的性能,是把复杂结构问题转化为遗传算法所能处理的关键。编码方法主要有:二进制编码、格雷码、符号编码和浮点数编码。

二进制编码是用一个二进制数表示一个染色体,二进制数中的每一位称为染色体的遗传因子,其位数由所要求的精度确定。二进制编码的优点是编码操作简单,后面的遗传操作容易实现,而且便于进行理论分析等。缺点是长度较大,对于一些个体编码位串比较短时,无法达到所要求的精度,如果长度较大时,精度虽然提高了但遍历空间急剧扩大,大大降低了算法的性能。

格雷码是连续的两个整数编码值只有一个码位不相同,其余一样。如十进制数5和6的格雷码分别为0111和0101,其二进制编码分别为0101和0110。

符号编码是指编码串中的表示是取自只有代码含义的符号集而无数值含义。符号集的组成可以是一个字母表,如{a,b,c,d,e,...},也可以是一个代码表,如{Y1,Y2,Y3,Y4,...}等。

3.2 生成初始群体

群体的初始设置并不复杂,它是通过随机产生若干个染色体的初始群体[3],每个染色体的组成应符合上述所选定的编码方案。这个我们可以称为遗传的第一代,以此为起点执行进化操作,直至优化准则终止条件,得到最优解。

3.3 适应度函数

在遗传和进化的研究领域,为了能够确定某个物种适应环境的能力,我们可以使用适应度来对其进行衡量和判断,具有存活和繁殖机会的当然是适应度较高的物种,适应度低的将被淘汰。因此在遗传算法中也同样用适应度来确定解的优劣,为此要根据所求问题构造适应度函数,它可以对问题中的每一个染色体进行度量,从而确定染色体的优良程度。它在算法中的作用是很重要的,将问题的标准评价以适应值来直观描述,对于最终获得最优解起到了决定性作用。一般情况下,适应度函数确定的依据为对约束条件违反情况加权求和,若用Yi表示约束条件i的值,若违反了其值为1,否则为0。其对应的权值为Xi,把所有违反约束的权值加起来,求其倒数,值越大说明违反约束条件的就越少,适应能力就越强,繁殖的机会就越大。适应函数可表示为

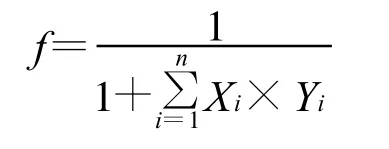
式中Xi—第 i个约束条件的权值;Yi=0表示无第i个约束条件的取值;f—适应度。

3.4 遗传操作

遗传操作[4]的方式主要三种:复制操作、交叉操作和变异操作。

复制操作其实是一种选择,就是根据每个个体的适应度值来选择,哪些个体是优良的能够有机会繁殖后代,哪些个体将被淘汰。这也符合生物进化的优胜劣汰、适者生存的原则,从而得到较为优质的后代。选择的原则一般可以根据适应度函数求得每个个体的适应度值,其值较大的个体能够存活,值较小的个体将被淘汰。赌轮选择是简单遗传算法常采用的机制,具体的说,首先求出群体中所有个体适应度的总和,计算方法如下:

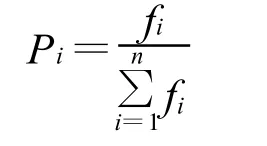
式中fi—第i个个体的适应度值;Pi—第i个个体的选择概率。

交叉操作是利用两个个体作为父母个体,对其两个个体中的部分代码进行交换,以便产生新的个体,这是优良个体获取的重要手段。现以单点交叉说明交叉的方法,设个体的编码为一个十位的二进制数,随机取其两个个体A和B,交叉点为第4位遗传因子,交叉操作后的A和B个体分别为A'和B',表示为变异操作就是改变个体上某个位置的数码,

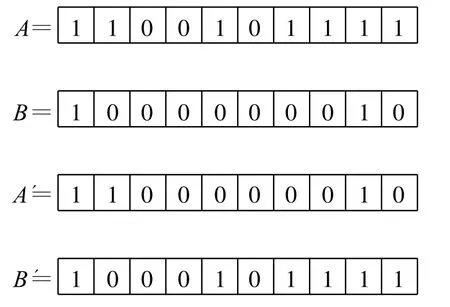
对于编码为二进制的个体,就是把相应位的0变为1,1变为0,如把上面的个体 A,从第五位开如进行变异操作,得到 A″。

变异操作主是防止有用解的丢失,确保对空间中重要点的遍历,使算法的全局收敛性增强。

3.5 算法参数

遗传算法在实际应用研究中,为了能更好地获得最优解,需要提前设定遗传算法的控制参数[5-6],包括主要参数和次要参数的设定。主要参数有算法的群体大小和执行算法的代数,次要参数是遗传操作的三种算法所对应的概率,分别是:复制概率、交叉概率和变异概率。

4 结束语

在遗传算法中其基本操作的要素是至关重要的,对于问题的描述要设置一定的编码形式给出,形成染色体,以便后面的遗传操作。对于问题的适应力处理要确定相应的适应函数,为个体的选择和优化提供依据。

[1]蔡自兴.人工智能及其应用[M].北京:清华大学出版社,2004.

[2]颜富强.遗传算法在数据挖掘中的应用研究[D].长沙:湖南大学,2008.

[3]吴晓虹.遗传算法在数据挖掘中的应用[D].桂林:桂林工学院,2008.

[4]李文科.基于遗传算法的数据挖掘技术的研究[D].南京:中南大学,2009.

[5]盛文峰.数据挖掘的遗传算法的研究与应用[D].上海:上海交通大学,2007.

[6]赵建峰.数据挖掘中一种基于遗传算法改进的ID3算法[D].武汉:武汉科技大学,2008.