具连续变量高阶中立型差分方程的渐近性

孙 静,刘志民

（河北工程大学 理学院,河北 邯郸 056038）

随着医学,生物数学,现代物理等自然科学和边缘学科的发展,出现了许多由差分方程描述的具体数学模型。近年来,在具有离散变量的差分方程的解的振动性研究方面的论文比较丰富[1-3],而具有连续变量的高阶差分方程渐近性的研究还不多,文献[4]主要研究了一类高阶方程的振动性,且给出了非振动解的渐近性的一个充分条件,严秀坤在文献[5]中以离散Knesor定理为基础讨论了一类高阶变系数非线性中立型差分方程的渐近性,本文应用反证法和数学归纳法,考虑具有连续变量的高阶差分方程的渐近性。

1 基本引理

式中 τ＞0是步长。

对于方程（1）,

令

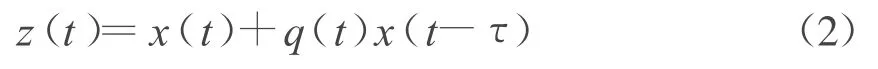
函数{y（t）}称为方程（1）的解,如果 y∈C（[t0-δ（t0）,+∞）,R）,当 t≥t0时,{y（t）}满足方程（1）。

首先给出下列条件:

（A）uf（u）＞0,u≠0

（B）对某个 t≥t0,有

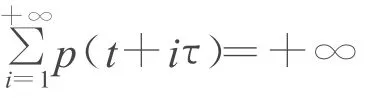
（C）0≤q（t）≤1

引理1 若{x（t）}是方程（1）的一个有界最终正解,设条件（A）和（C）成立,则当 d是奇数时

则当d是偶数时

2 主要结果及其证明

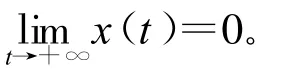
证明不妨设{x（t）}是方程（1）的一个最终正解,则存在充分大的自然数t1≥t0,使得式（3）成立,又由条件（A）可知

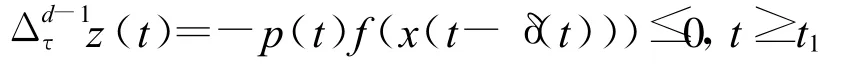
成立。因为d是奇数,由引理1可知式（3）和

成立。

由Δτz（t）＜0知{z（t）}最终单调递减,当 t→+∞时,{z（t）}存在有限的非负极限;由条件（C）和式（2）知,{x（t）}也存在有限的非负极限l1,即

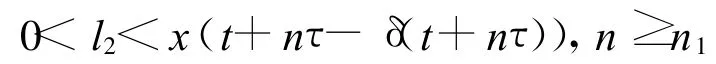
由于函数f（u）是单调非减的及条件（A）,有

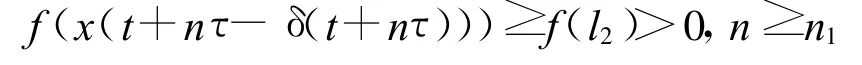
从而由方程（1）有

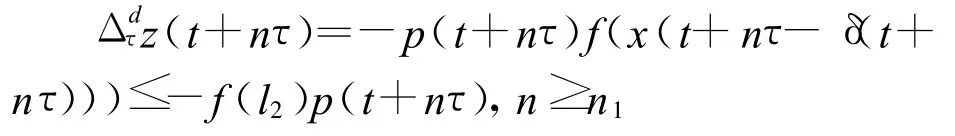
将上式的两边对n从n1到n求和,得

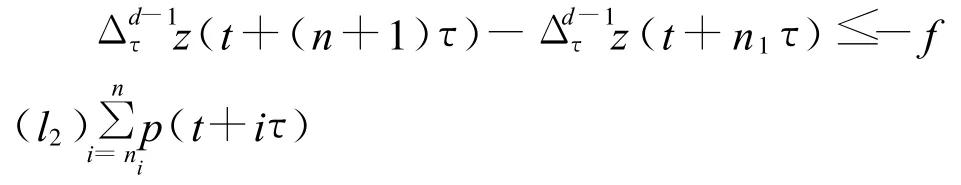
由条件（B）知

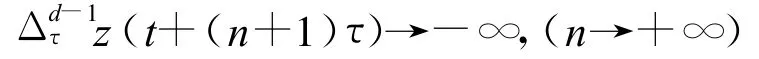
当{x（t）}是方程（1）的最终负解时,可同理证明。证毕。

证明不妨设{x（t）}是方程（1）的一个最终正解,则存在充分大的自然数t1≥t0,使得式（3）成立。因为d是奇数,由引理1可知式（3）和式（5）成立,再由上面定理可知,式（6）成立。

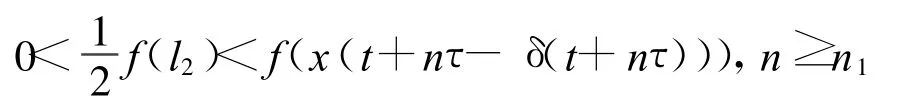
从而由方程（1）有

类似于定理2的证明,可知最终有

当{x（t）}是方程（1）的最终负解时,可同理证明。

定理3 若{x（t）}是方程（1）的有界非振动解,设条件（A）成立,且 d是偶数,则 t→∞时,{x（t）}收敛于某有限数值。

证明不妨设{x（t）}是方程（1）的有界正解,则由引理1得Δτz（t）＞0最终成立。所以{z（t）}是最终单调递增的,又因为{x（t）}有界,因而{z（t）}有界,所以 t→+∞时,{z（t）}存在正的有限极限,从而{x（t）}存在正的有限极限。

当{x（t）}是方程（1）的有界负解时,可类似证明{x（t）}存在有限的负极限。证毕。

3 结论

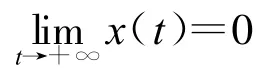
[1]韩振来,李秀珍,从今明,等.一类具有连续变量的三阶非线性时滞差分方程的振动性判据[J].济南大学学报:自然科学版,2003,17（4）:334-336.

[2]孙书荣,韩振来.一类具有连续变量的二阶中立型差分方程的振动性[J].工程数学学报,2005,22（5）:943-946.

[3]刘志民,孙静.具有连续变量二阶中立型差分方程的振动性及其有界解[J].河北工程大学学报:自然科学版,2009,26（2）:109-110.

[4]唐清干,曾玲.高阶中立型差分方程的振动性及其非振动解的渐近性态[J].数学杂志,2000（20）:207-210.

[5]严秀坤,张卓飞.高阶非线性中立型差分方程的渐近性态[J].湘潭大学自然科学学报,2006,28（1）;20-23.