改进型混沌粒子群算法求解函数均值问题

王晓敏,刘宏伟,李石妍

（1.河北工程大学 机电工程学院,河北 邯郸 056038;2.河北工程大学 文学院,河北 邯郸 056038）

基于对鸟群捕食行为的仿生,Eberhart博士和Kennedy博士于1995年提出了粒子群优化（Particle Swarm Optimization,PSO）算法[1-2],该算法基于群体智能,是一种简洁高效的随机优化算法,但存在容易陷入局部最优、并且搜索精度不高的缺点。混沌是在非线性系统中普遍存在的现象,混沌运动具有对初值的高度敏感性、运动轨迹的遍历性和随机性等特点,它能在一定的范围内按自身的规律遍历每一个轨道,既不自我重复又不自我交叉。混沌算法和粒子群优化算法各有优缺点,混沌算法的全局搜索能力较强,而粒子群算法具有较强的局部搜索能力。近几年来,很多学者把两种算法的优点融合在一起,提出了多种混合算法:文献[3]利用混沌运动随机性、遍历性和初值敏感性,提出了一种混沌粒子群优化算法并应用于多阈值图像分割中;文献[4]针对传统的简单粒子群算法易陷入局部最优的缺陷,提出了一种改进的混沌粒子群优化算法,该算法根据混沌算法遍历性的特点,选择合适的混沌映射提取基本粒子群初始种群,使粒子均匀分布在解空间,当基本粒子群陷入早熟时,混沌粒子群在最优解周围的区域内进行混沌搜索,取代原来种群中的部分粒子,带领种群跳出局部最优;文献[5]针对基本粒子群优化算法易陷入局部极值和进化后期收敛速度缓慢的问题,提出基于Tent混沌序列的粒子群优化算法,应用Tent映射初始化均匀分布的粒群来提高初始解的质量,设定粒子群聚集程度的判定阈值,并引入局部变异机制和局部应用Tent映射重新初始化粒群的方法,增强算法跳出局部最优解的能力,有效避免计算的盲目性,从而加快算法的收敛速度。

但是融合混沌方法的混合型粒子群算法的求解精度尚不尽人意[6-7]。本文将有限作用域的机制引入到粒子群的寻优过程中,以有限作用域作为边界,将粒子群体分成不同的两部分:作用域内的粒子被用以提高搜索精度,作用域外的粒子被用以增加群体对可行域的开发程度。

1 算法优化

1.1 基本粒子群优化算法

在标准PSO算法中,假设在一个D维的问题空间中,包含m个粒子,每个粒子作为搜索空间中待优化问题的一个可行解,通过粒子之间的协作与竞争来寻找问题的最优解。在第 t次迭代中,第i个粒子的当前位置表示为xi（t）=（xi1（t）,xi2（t）,…xid（t））,当前速度表示为vi（t）=（vi1（t）,vi2（t）,…vid（t））。在每次迭代中,粒子个体搜索到的最佳位置用pbi（t）=（pbi1（t）,pbi2（t）,…pbid（t））表示,记作 pbest,称为个体最优;群体中所有粒子搜索到的最佳位置用gb（t）=（gb1（t）,gb2（t）,…gbd（t））表示,记作 gbest,称为全局最优。

优化问题的过程可看作粒子不断更新的过程,每个粒子以当前速度、个体最优和全局最优来调整自己的飞行速度vid（t+1）和方向xid（t+1）,通过迭代n代,最终以第n代的全局最优值作为问题的解。

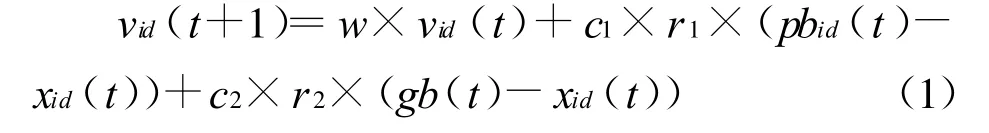
其中,i=1,2,…m;d=1,2,…D;r1,r2为（0,1）上的随机数;常数c1,c2为学习因子,表示粒子受个体认知和社会认识的影响程度,调节向pbest和gbest方向飞行的最大移动步长,式（1）中的w×vid（t）部分称为动量部分,表示粒子对当前自身运动状态的信任程度,w称为惯性权重（inertia weight）,使其依据自身速度进行惯性运动;c1×r1×（pbid（t）-xid（t））部分称为个体认知（congnition）部分,代表粒子飞向自身的最佳位置;c2×r2×（gb（t）-xid（t））部分称为社会（social）部分,表示粒子间的信息共享与相互协作,它引导粒子飞向群体中的最佳位置。这3个部分之间的相互平衡和制约决定了算法的主要搜索性能。

通常w在区间[0,1]中。不同的 c1,c2描述了粒子对可行域的开发程度,r1,r2是均匀分布在（0,1）之间的随机数。vi在区间[vmin,vmax],当粒子的速度超过边界时,设置其为边界值,vmin,vmax按可行域大小进行设置。

1.2 混沌与混沌序列

混沌是被提出用以分析对初始设置非常敏感的动态系统的一种理论工具。它是由Lorenz在1972年提出的。混沌序列有非常良好的非线性性质,比如对初始值敏感,对可行域的遍历等。这些性质有利于分析和应用于具有多极值的复杂系统。

Logistic是混沌理论中主要的映射。在确定初始值和映射参数后,序列便被确定。Logistic序列的表达式为

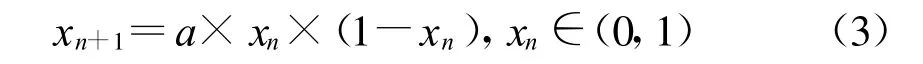
a=3.995,x0=0.640的Logistic序列和均匀分布的随机数的对比分布图如图1所示。Logistic序列主要分布相对在[0,1/3）和（2/3,1]中。这与均匀分布的随机函数相比,可以使粒子在初始分布时局有更大的覆盖范围。在粒子的速度更新过程中,更具多样性。

1.3 初始分布对搜索过程的影响

不适当的粒子初始分布会严重影响PSO的搜索效率。在PSO的搜索过程中,随着迭代的进行,粒子的搜索范围会不断地变小,如图2所示。

在图2中,4个子图分别代表标准粒子群在搜索Rosenbrock函数时,不同迭代次数时的粒子分布。各个子图中的不规则多边形表示粒子群体有可能搜索到的可行域范围,因为粒子的飞行速度在初始化过程中是随机分布的,所以此范围可能有扰动,但与多边形相差不会很大。图2中,阴影在不断的缩小,最终聚集在最优值（1,1）点（对应于不同的测试函数,最优点不同）。这说明随着迭代次数的增加,粒子更加注重在局部进行搜索,提高搜索精度,而基本放弃了对可行域的开发。

在每次的迭代过程中,算法均是基于如下的假定:最优点会在 Ci中,Ci为在第i次迭代过程中,包含所有粒子的最小圆,Rci为半径,我们应用Rci来评判Ci的大小。Rci趋近于 0,既 pbest趋近于gbest,X趋近于gbest。其中存在的问题是gbest只是整个群体所搜索到的最优值。gbest也是其中一个粒子的Pbest,所以只要粒子的初始分布 C0没包含优化问题的全局最优点,比如,当粒子的初始分布只限定在可行域的一部分,如果粒子只在一半的可行域中分布,粒子的作用域并没有覆盖最优值点（即最优点并不在圆中）,则PSO在搜索过程中很难再找到优化问题的全局最优点。所以在粒子群优化的改进过程中,在初始分布时,尽可能的扩大其作用域覆盖范围,或使在一定的迭代次数内,粒子的作用范围不会收缩的很快,这有利于粒子对整个可行域的开发,并搜索到全局的最优解。

1.4 粒子的作用域

有限作用域是指在函数值小到一定程度（设定的阈值）的粒子所组成的区域,在此区域中,可能存在函数值大于阈值的粒子。本文对有限作用域内的粒子以式（1）更新速度,而对有限作用域外的粒子以其自身的最优值作为目标进行更新,如式（4）所示。

式（4）中,c3×r3×（pi-xi（k））代表粒子飞向自身的最好位置;c4×r4为粒子的搜索扰动,即之前的粒子在局部的随机扰动,此项与粒子所在位置无关,只与粒子本身有关。粒子子群相当于在可行域中的随机飞行,以广度为目的继续开发可行域。有限作用域是随着迭代次数增加而不断的减小的,这样做的目的在于在迭代的后期,仍然存在粒子在开发可行域,而有限作用域内的粒子会更加专注于提高全局最优值的精度。

1.5 求解过程

粒子群算法的每一步都根据前一步所获得当前最好的点与自身寻找的最好的点进行该步的调整。通过此方式一步一步地调整,最后把问题的最优值找出来。基于这样的思想,任何一个问题,只要其作为最优的个体与作为局部最优的个体是具有某种特性的,那么按粒子群算法的迭代方式,最终就可以把具有某种特性的解求出来。函数的均值,是具有某种特性的点,因此,可以利用粒子群算法进行求解。

对于函数y=f（x）,x∈[a,b],利用粒子群算法求出其均值的关键是怎样确定粒子群中的整体均值、局部均值。因为在均值未求出的情况下,很难确定哪个粒子更接近问题的均值。给出整体均值、局部均值的不同的算法将给出不同的粒子群求均值的算法。本文以最接近当前各粒子的适应度为整体均值、以一定的组合方式给出局部均值。

本文构造的利用粒子群算法求均值的基本过程如下:

步骤2:以Logistic序代替随机数,初始化粒子群;

步骤3:更新有限作用域;

步骤4:以混沌序列代替随机数;

步骤5:以一定的阈值把粒子分为两类:有限作用域内的粒子集合和有限作用域外的粒子集合;

步骤6:用式（1）更新有限作用域内的粒子的速度;用式（4）更新有限作用域外的粒子的速度;

步骤7:用式（2）更新粒子的位置;

步骤8:确定局部均值。

其中rand（）是[0,1]之间的一个随机数,比较 f（xi）,f（pid）,取其中离 qi最近的为新的f（pid）,从而得到局部均值点pid与局部均值f（pid）。

步骤9:确定整体均值。

步骤10:若满足终止条件,则返回当前最优粒子;否则,k=k+1,转到步骤3。

2 算例分析

为了验证方法的有效性,分别取以下3种不同类型的函数进行测试:

算法初始种群都为100、迭代的代数都为100代;参数 ω,η1,η2分别取为:0.1,0.2,0.2;总共计算100次,每次得到一个平均值的结果,100个结果的平均值记为 af、最好值记为 of,标准差记为σ,精确值 p,结果列于表1。

表1 三个测试函数的实验结果Tab.1 Experimental results of three test function

从以上的结果与演化曲线图可以看出,本文方法能比较精确地求出函数在某一区间段上的平均值。这是由于本文对粒子群算法的局部极值与整体极值作出了合理的定义,使得粒子群算法能朝着函数的平均值进行运动,虽然有时会在平均值附近振荡,但最终都能把平均值求出来。

3 结论

1）通过以混沌序列初始粒子分布,粒子以更大的概率分布靠近可行域的边界并覆盖最优值点,并提高粒子群体的多样性。

2）该算法将有限作用域的机制和混沌序列引入到速度更新过程中,增加了种群多样性,提高了粒子对可行域的开发程度。

[1]KENNEDY J,EBERHERT R.Particle swarm optimization[C/OL]//Proceedings IEEE International Conference on Neural Networks.[2011-01-22].http://ieeexplore.ieee.org/xpl/freeabs-all.jsp?arnumber=488968.

[2]周书敬,薄涛,史三元.混合算法在轻钢结构优化设计中的应用[J].河北工程大学学报:自然科学版,2011,28（2）:71-74.

[3]蒋艳会,李峰.基于混沌粒子群算法的多阈值图像分割[J].计算机工程与应用,2010,46（10）:175-177.

[4]刘玲,钟伟民,钱锋.改进的混沌粒子群优化算法[J].华东理工大学学报:自然科学版,2010,36（2）:267-272.

[5]田东平.基于Tent混沌序列的粒子群优化算法[J].计算机工程,2010,36（4）:180-183.

[6]张勇,巩敦卫,张婉秋.一种基于单纯形法的改进微粒群优化算法及其收敛性分析[J].自动化学报,2010,35（3）:289-298.

[7]CUI Z H,CAI X J,ZENG J C,et al.Apical-dominant particle swarm optimization[J].Progress in Natural Science,2011,18（2）:1577-1582.