基于大涡模拟方法的多层动网格技术识别平板气动参数
刘祖军,葛耀君,杨詠昕
(同济大学 桥梁工程系,上海 200092)
目前桥梁风工程中的气动导数一般通过风洞节段模型试验来获得,采用的方法主要有自由振动法和强迫振动法。前者通过给模型一个初始位移或脉冲激励,使其在气动力和结构阻尼下做自由衰减运动,后者采用机械装置驱动模型作可控频率、振幅的强迫运动,测得模型位移、加速度或表面压力等时程,通过各种参数识别方法获得气动导数。自由振动法试验设备简单,识别精度低,折减风速范围小,强迫振动法虽然可以克服这些缺陷,参数识别精度高,能得到大范围折算风速下的气动导数,但是由于其试验设备要求高,在工程中应用并不很广泛[1,2]。随着计算机硬件能力的提高和计算流体动力学的发展,采用数值模拟方法进行气动导数识别在断面选型中应用越来越广泛。
数值模拟[3]采用动网格方法识别气动导数如果仅控制结构表面一层的网格节点运动就要求网格划分得足够细,结构振幅不易过大,否则容易出现网格节点间的间距过小,导致网格形成很小的锐角或网格空间位置发生翻转而产生错误无法计算,而振幅太小不能模拟结构体的真实振动情况,为了兼顾振幅与网格密度,本文采用多层动网格技术来解决这一问题。为考虑湍流影响采用大涡模拟方式(LES)求解N-S方程,通过对流体计算软件fluent的二次开发,利用其用户自定义函数描述结构的运动状态,采用最小二乘法拟合气动力时程曲线来识别断面的气动导数。
1 基于多层动网格的气动导数识别
1.1 流体动力学计算
流体域内计算结构在一个振动周期内作用在其表面的气动力是通过将结构表面的流体网格节点的简谐振动位移等分的离散到N个时间步上,将第i个时间步上变形后的节点坐标作为第i+1步的网格文件,每个时间步上求解N-S方程。
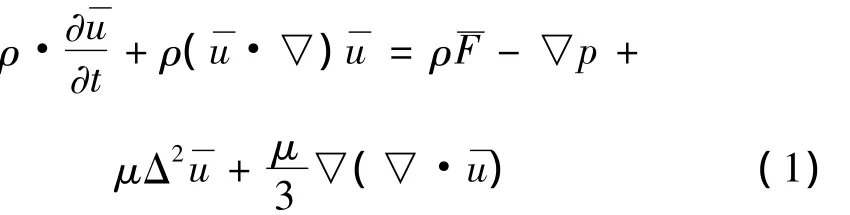
湍流[4]的存在使得求解上述N-S方程变得十分困难,通过大量学者的不懈努力已提出较多的湍流模型,较为常见的有:雷诺时均方法(RANS),直接数值模拟(DNS)以及介于二者之间的大涡模拟(LES)。由于RANS方法平均的结果是将时空变化的细节一概抹平,丢失了包括在脉动运动中的大量信息,并且为了使N-S方程封闭,提出了Reynolds应力模型和涡粘模型,这些模型有一定的局限性,都存在着对经验数据过分依赖和预报精度较差的特点。DNS采用计算机直接数值求解三维非定常N-S方程,对湍流瞬时运动直接模拟,可认为是一种精确的方法。主要用做湍流基础研究,目前仅限于科学研究领域。
大涡模拟[5-7]是放弃了对全部尺度范围内的涡运动进行直接模拟的梦想,改为只对尺度大的涡运动通过数值方法直接求解N-S方程,对尺度小的涡运动不直接求解而是通过建立模型模拟小涡运动对大涡的影响。其具体实现过程为:首先通过滤波方法将小尺度涡和大尺度涡分离开来,即将流动划分为低频可解和高频不可解(亚格子部分)两部分。对不可解部分建立亚格子尺度模型来模拟。目前常用的亚格子模型主要可以分为三类:涡粘模型,相似性模型和混合模型。本文CFD计算时采用Smagorinsky-Lilly涡粘形式的亚格子雷诺应力模型其表达式如下:
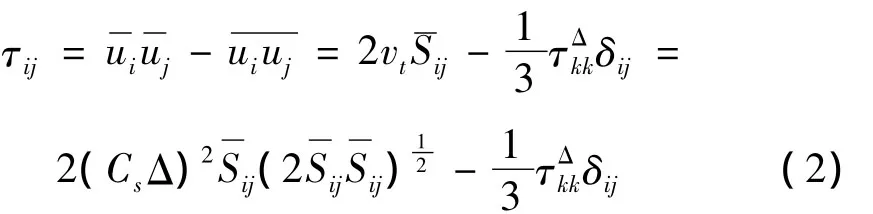
Smagorinsky模型相当于混合长度形式的涡粘模型,其中CsΔ相当于混合长度,Δ为过滤尺度,Cs为Smagorinsky常数,Lilly于1987年通过计算建议 Cs≈0.18。
1.2 动网格空间守恒条件
采用动网格方法必须满足几何守恒条件,Thomas和Lombard明确提出了用来确定网格速度的法则也称为空间法则,该法则直接从连续方程中推得:
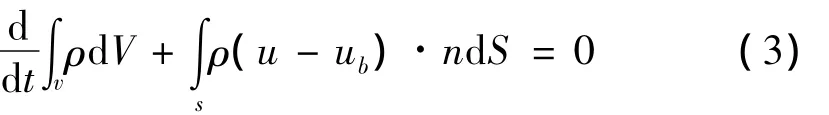
式中流体速度为常数,因此几何守恒法则表达为:
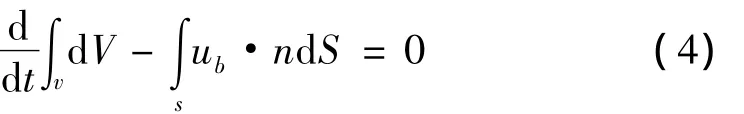
因此只要是动网格问题都必须保证网格速度满足几何守恒法则,否则可能在动网格计算过程中导致人为的质量源项。
本文提出的多层动网格方法是通过设定每层动网格做刚体的平动或扭转运动,相邻动网格层之间通过弹簧近似方法连接形成变形网格层,变形网格区,网格只发生变形没有网格速度。因此只需证明发生刚体平动的动网格层满足几何守恒条件即可。
如图1所示的控制体中,w,s,e,n分别为运动前网格的四个边界,当网格发生竖向平动时,边界s平移到s'的位置,n平移到n'位置,由于是刚体平移,故Δy1=Δy2,边界w和e没有变化。
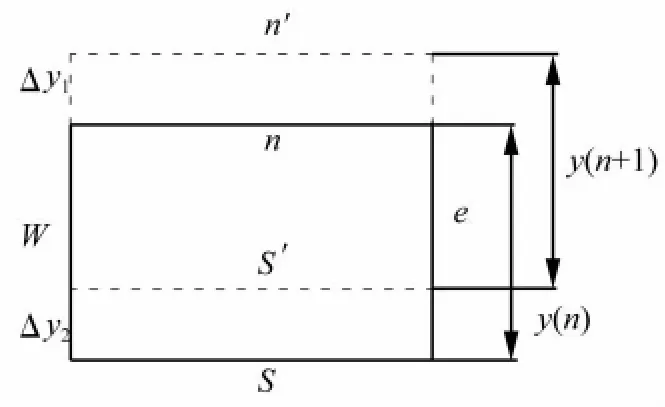
图1 网格运动图示Fig.1 The motion of mesh
在图示控制体上,对连续方程进行离散;
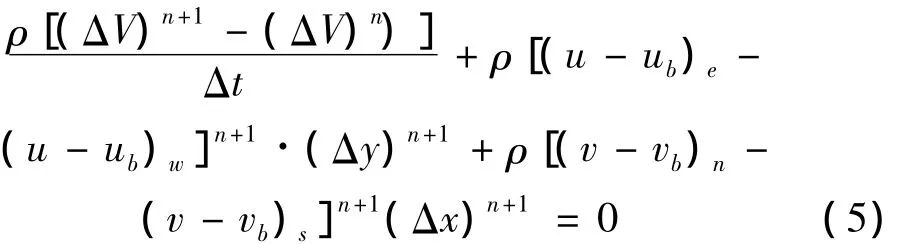
式中:u,v代表笛卡尔坐标系下的水平速度分量和竖向速度分量,n和n+1对应两个速度时刻,ΔV为控制体体积,假定流体运动速度不变,因此有关流体速度项可以抵消,上式简化为:
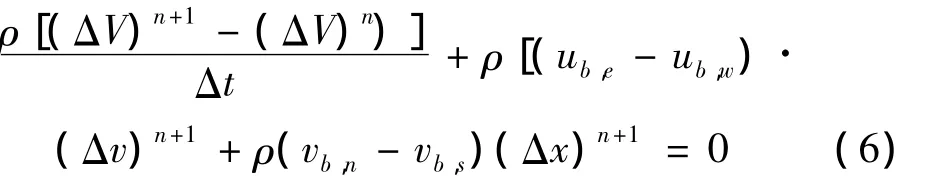
按照前面定义网格做竖向刚体运动时:
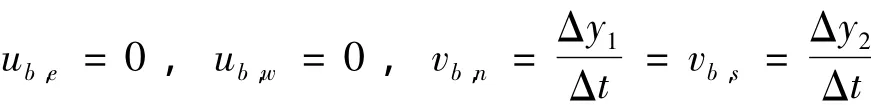
代入上式则有:
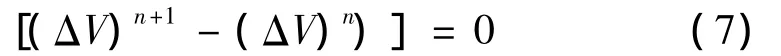
故每层网格的运动都能保证几何守恒法则。
1.3 多层动网格的实现
在工程实际问题中经常遇到流体与固体相互耦合作用的情况,通常计算域的边界是运动的,从而使计算域的形状随时间变化。动网格技术随时间变化对流场模型进行更新。在某一时刻,边界发生一定位移后,边界内部的网格应该如何确定,已经有很多研究成果。较常用的有弹簧近似法,弹性体法,采用Laplace方程控制的方法,其中以弹簧近似方法应用最多。
弹簧近似方法原理简单[8](图2),使用方便。在实际应用中当边界位移较大时,容易出现网格节点间的间距过小,从而导致网格形成很小的锐角(图3)或网格点的空间位置发生翻转(图4),导致计算失败。因此在CFD计算时仅控制结构体表面一层网格节点运动具有一定的局限性。如果要模拟出流体域中的附面层不同大小的涡时就要将流体的网格划分得足够细,一般结构表面的网格在0.00001 m的数量级,所以结构表面节点空间位置的变化对其周围流体单元的形态影响较大。结构振幅较大,容易导致网格变形过大,而产生错误无法计算;振幅太小,不能模拟结构的真实振动情况,振幅与网格密度不能兼顾,因此需要通过多层动网格技术来实现。
多层动网格方法将结构的振动位移按照一定的比例加到结构周围的N层网格节点上,一定程度上加大了结构的可移动范围,使流体网格在N层范围内实现运动。通过设定每层动网格层做刚体的平动或扭转运动,相邻动网格层之间通过弹簧近似方法连接形成变形网格层,由于采用多层动网格后相邻网格的平动速度差值变小,因此变形区的网格不容易出现网格翻转或过小尖角,易保证网格质量。多层动网格的具体做法是:按照各层间的比例关系给出各层节点的运动位移(如图5),结构表面距离为Ri的第i层网格节点的位移最大等于结构的振幅即Si=Am,结构表面距离为Rn的第n层网格位移为0即Sn=0,位于这两层之间的第j层网格节点位移进行线性插值,这样就实现了运动结构周围流体网格的多层运动。这样既提高了网格可动范围,又减小了相邻两层动网格之间的相对位移,避免了网格位移过大造成的计算失败。
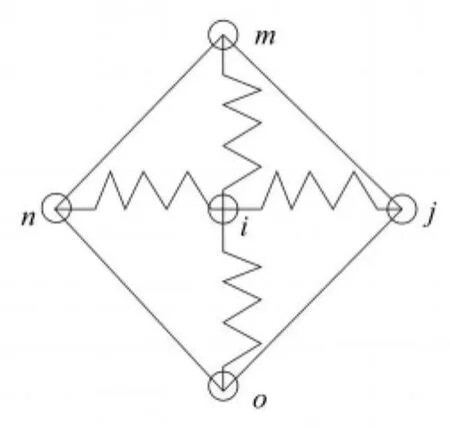
图2 动网格弹簧节点连接Fig.2 Spring node of dynamic mesh
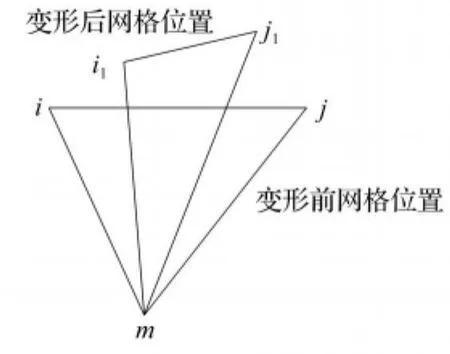
图3 网格变形后出现过小的尖角Fig.3 Produce small cusp after deformation mesh
图4 网格变形后出现翻转Fig.4 Produce flip after deformation mesh
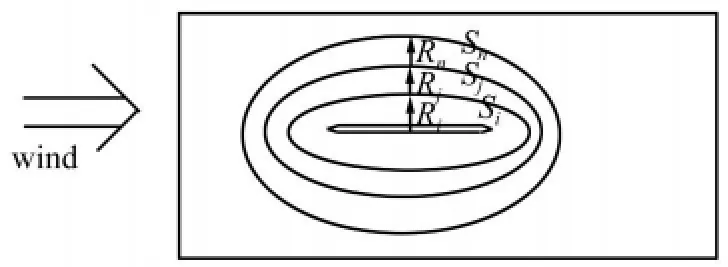
图5 多层动网格示意图Fig.5 The multi-layer dynamic mesh
1.4 气动参数的识别原理
气动力可以用气动导数来表示,而气动导数是系统运动折减频率的函数,其函数关系决定于断面的气动外形,一般很难有解析表达式,大多通过节段模型风洞试验来识别。气动力用试验测到的8个气动导数表示为:
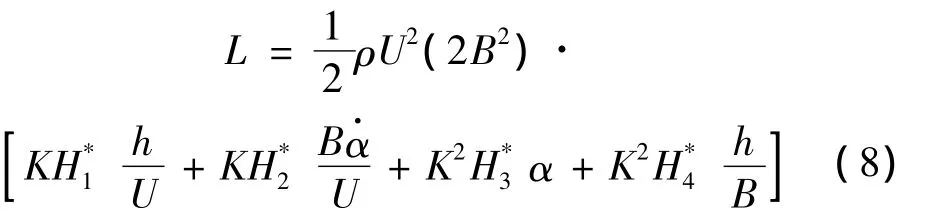
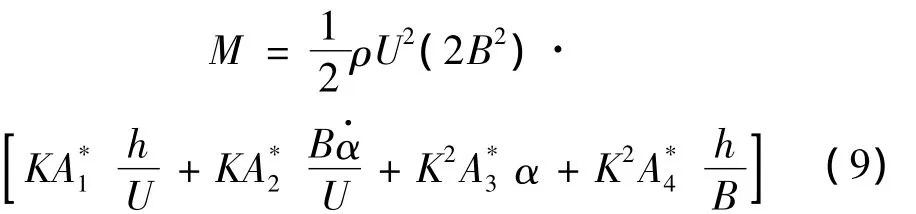
理想平板是完全理想化的流线型结构,可以通过Theodorson建立的理论公式得到振动平板所受到的气动力,从而导出气动导数理论值。平板振动时所受到的非定常气动升力和升力矩可表示为:
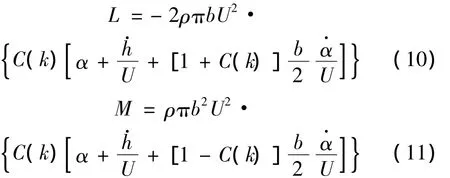
式(8)~式(11)中:U为来流速度,B=2b为平板宽度;K=ωB/U为折算频率;ω为振动频率;h,a分别为平板竖向位移和扭转角;
C(k)=F(k)+iG(k)为Theodorson函数;
根据Theodorson建立的上述自激力公式可以导出平板断面的8个气动导数,并表达为折减频率函数:
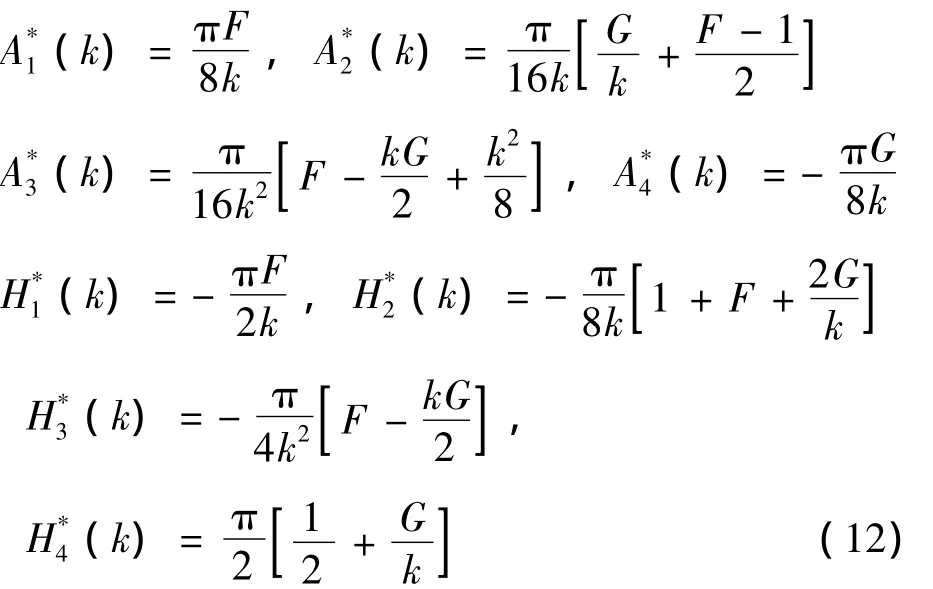
强迫平板单独作竖向正弦振动或扭转正弦振动,将结构表面压力值和摩阻力沿表面积分,可得到在绝对坐标系里的气动升力和弯矩。然后由得到的气动力和式(8)-(9)中对应的气动导数之系数,根据最小二乘法,即可得到相应的气动导数。竖向振动时采用上述方法可以提取H,4个气动导数,做扭转运动可以确定另外的4个气动导数
2 平板的颤振导数识别
通过流体分析软件Fluen[9]的用户自定义函数来描述模型的运动状态,并利用其大涡模拟的湍流模式进行数值计算(图6)。
图6 数值计算流程Fig.6 The process of Numerical
平板模型如图7,宽高比22.5,模型前后缘尖锐,小攻角下流线形特征明显,流场计算域外边界为矩形,参考同济大学TJ-1风洞 尺寸设为2×6 m。

图7 平板模型图Fig.7 The model of flat plate
平板竖向振动的振幅0.08m,扭转幅角3°。入口为速度边界条件,入口风速为U=5 m/s,出口为压力边界条件,表压设为0,参考压力点在出口边界中心处;上下边界设为对称边界,以加快计算速度,时间步长设为0.001 s。建立二维计算模型,网格线与物面平行,周向网格线在靠近物面附近加密,离开物面间距逐渐加大。交于物面的网格线在模型前后缘位置均加密.网格数为3.02万。
模型从零攻角的平衡位置开始运动.图8、图10是低折算风速(Vr=5)下的运动,图9、图11是高折算风速(Vr=20)下的运动.平板分别作纯竖向振动和纯扭转振动,气动力数据在2个周期后开始采集。从图8-图11可知,在这两种振动情况下,升力系数和升力矩系数均表现为对无量纲时间零均值的一次稳态谐波曲线特性,升力、升力矩与位移之间的良好的线性关系表明流场与平板一起进入谐振动状态,流场没有出现不稳定情况。
在不同的折算风速下,分别计算平板做纯竖向振动、纯扭转振动的气动力,当气动力的变化趋势变得平稳时,开始采集气动力数据,并用最最小二乘法提取气动导数。本文比较了计算得到的气动导数与通过Theodorsen理论[10]推导出的气动导数之间的差别,见图12,从图中各颤振导数值的比较来看,当折减风速较低时,各导数值吻合较好,随着折减风速增大,各导数值偏差增大,其中和的误差相对大些,但均与通过Theodorsen理论导出的气动导数值有合理的一致性,其中几个关键导数及吻合的很好。
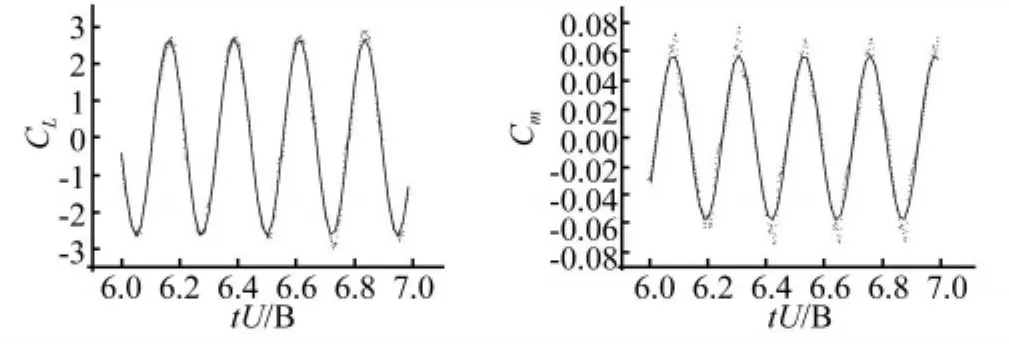
图8 低折算风速下纯竖向运动产生的气动升力系数和升力矩系数时程Fig.8 Lift and moment coefficients Vs time on heaving vibration at lower reduce wind speed
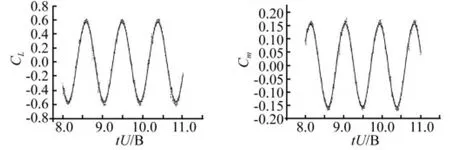
图9 高折算风速纯竖向运动产生的气动升力系数和升力矩系数时程Fig.9 Lift and moment coefficients Vs time on heaving vibration at higher reduce wind speed
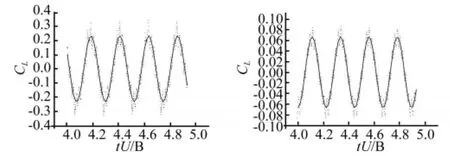
图10 低折算风速纯扭转运动产生的气动升力系数和升力矩系数时程Fig.10 Lift and moment coefficients Vs time on pitching vibration at lower reduce wind speed
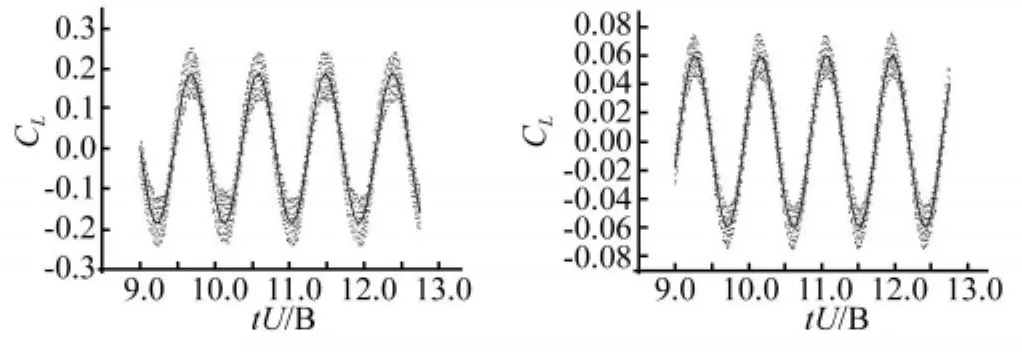
图11 高折算风速纯扭转运动产生的气动升力系数和升力矩系数时程Fig.11 Lift and moment coefficients Vs time on pitching vibration at higher reduce wind speed
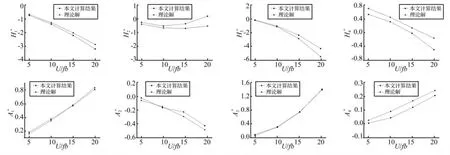
图12 平板气动导数Fig.12 Flutter derivatives of flat plate
3 结论
本文通过对流体计算软件fluent的二次开发,利用其提供的用户自定义函数模块,结合动网格技术实现了平板的气动导数识别。由于固体模型在流场中运动受到流体网格尺寸限制,当模型运动幅度较大时,常会造成网格的变形过大,导致计算无法进行。针对这一问题,本文采用了多层动网格方法较好地解决了这一问题。能较好的兼顾模型振幅和网格密度。采用本文方法所获得的计算结果与通过Theodorsen理论导出的平板气动导数具有良好的一致性。
[1]Scanlan R H,Tomko J J.Airfoil and bridge flutter derivatives[J].Journal of Engineering Mechanics Division,1971,97:1717-1737.
[2]Yang Yongxin,Ge Yaojun,Xiang Haifan.Investigation on fluttermechanism oflong-span bridgeswith 2d-3DOF method. WINDANDSTRUCTURES,2007,10(5):421-435.
[3]Chen Z,Hong L,Xiaofeng W.Full function numerical methodfor flow over a self-excited vibrating Body[J].Tsinghua Science and Technology,1999,4(4):1688 -1691.
[4]Fasel H F,Seidel J,Wernz S.A Methodology for simulations ofcomplex turbulentflows [J]. Journalof Fluids Engineering,2002,124(5):933 -942.
[5]Kalttenbach J H,Schumann U,Gerz T.Large eddy simulation of turbulent diffusion in stably-stratified flow[J].Fluids Mech,1994,280:1 -40.
[6]Kondo K,Murakami S,Mochida A.Generation of velocity fluctuations for inflow boundary condition of LES,[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,67:51-64.
[7]Tetsuro Tamura,Yoshiyuki Ono.LES analysis on aeroelastic instability of prisms in turbulent flow[J].Journal of Wind Engineering and IndustrialAerodynamics,2003,91:51 -64.
[8]郭 正,李晓斌.用非结构动网格方法模拟有相对运动的多体绕流[J].空气动报,2001,19(3):28-35.
[9]王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2004.
[10]Theodorsen T.General theory of aerodynamic instability and the mechanism of flutter[R].NACA Report,1935.

