碰撞效应对非规则梁桥横向地震反应的影响

徐略勤，李建中，吴陶晶

(同济大学 土木工程防灾国家重点实验室，上海 200092)

通常为了在山区跨越鸿沟深壑而修建的桥梁，由于受地形地貌的限制，其下部结构高度往往互不一致，墩高的不一致极易导致全桥结构横向刚度分布的不均匀，在地震作用下，上部结构的横向惯性力在下部结构的分配也参差不齐，高度较矮的桥墩由于刚度较大通常会吸收相对更大的横向地震力。板式橡胶支座的采用有助于缓解各墩受力不均带来的难题，但板式橡胶支座在使用不当时容易出现滑动或脱空现象，在地震作用下，这些现象愈发明显，而且往往造成很大侧向位移，引起上部梁体的滑落。为了限制梁体的侧向移位，挡块的运用呼之而出。防震挡块的运用在降低上部结构发生横向落梁的可能性的同时也增大了梁体发生横向碰撞的概率。事实上，在强地震作用下，碰撞现象在桥梁结构中普遍存在，国内外许多桥梁震害表明碰撞是引起结构失效甚至破坏的主要原因之一［1］。

本文着眼于考虑上部梁体与抗震挡块间横向碰撞效应对采用板式橡胶支座的山区非规则梁桥横向地震反应——主要是各墩横向地震剪力分布规律的影响。通过对一座桥例建立考虑横向碰撞效应的动力分析模型，比较分析了碰撞效应的影响，并讨论了在各种不同碰撞条件下，横向地震力分配规律的变化，得到的一些结论和规律可供桥梁的防震和加固参考。

1 结构动力分析模型

为了探究地震作用下主梁与挡块间的碰撞效应对非规则梁桥横向惯性力分配的影响，需要通过建立能恰当反映结构动力特性的实例有限元模型进行结构的地震响应分析。为此，本文选择了一典型山区非规则连续梁桥(如图1)作为代表进行相关的探索。图1所示的五跨连续梁桥，其上部结构为跨度30 m的连续箱梁，梁高1.8 m，桥宽8.5 m;下部结构采用圆形独柱墩，直径为2 m，墩高分别为9 m、20 m、15 m、11 m，墩顶盖梁采用矩形截面，其尺寸长×宽×高为6 m×2 m×1.5 m，每个桥墩盖梁上均分别安置两个板式橡胶支座，盖梁两侧各设置一个钢弹性抗震挡块，以防止主梁在强震作用下因横向位移过大而发生橡胶支座脱落甚至落梁等震害。

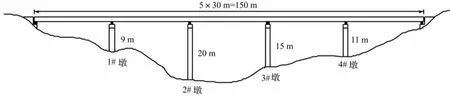
图1 某山区五跨连续梁桥Fig.1 Elevation view of a typical nonstandard girder bridge

本文采取了实效同时也能较真实地反映结构实际地震响应的方法建立该桥的分析模型，模型中考虑了橡胶支座的水平剪切变形作用，主梁与挡块间缝隙的闭合以及碰撞效应。由于重点考察碰撞效应的影响故对桥梁结构的桩土共同作用以及桥台与背填土间的共同作用未予考虑，同时认为桥墩处于弹性，故桥墩和主梁均采用线性杆单元模拟，单元的质量采用堆积集中质量表示，橡胶支座采用线性弹簧连接单元模拟，混凝土结构的阻尼比取为5%，在进行线性和非线性时程分析时，采用Rayleigh阻尼。

1.1 橡胶支座的模拟

板式橡胶支座一般由若干层薄钢板和氯丁橡胶叠合组成，用以提供竖向支承和水平剪切刚度。一般认为板式橡胶支座在地震作用下的耗能能力非常小可以忽略，因此可模拟成线性连接单元，单个橡胶支座的水平剪切刚度可以通过下式确定:

式中，kb1、Gd、Aτ和∑t分别表示单个橡胶支座的水平剪切刚度、动剪切模量、剪切面积和橡胶层的总厚度。单个桥墩上支座的总水平剪切刚度取为:，其中ni为该桥墩上橡胶支座的个数，在本桥例中取=1.0 ×104kN/m。

1.2 碰撞效应的模拟

由于橡胶支座的剪切变形，主梁在强震作用下可能会发生较大的侧向移位，引起主梁与挡块之间的碰撞。对地震作用下桥梁结构的碰撞问题国内外有不少学者进行过研究［2－6］，目前对桥梁结构纵桥向伸缩缝处相邻梁体间的碰撞以及横桥向梁体与挡块等限位装置间的碰撞效应的模拟采用最多的是接触单元(如图2所示)。接触单元的非线性力－位移关系可表示为:

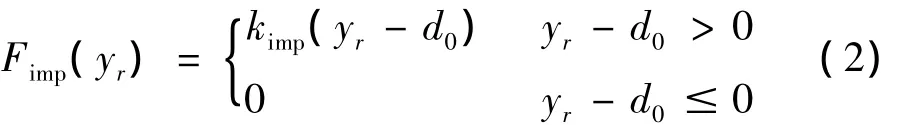
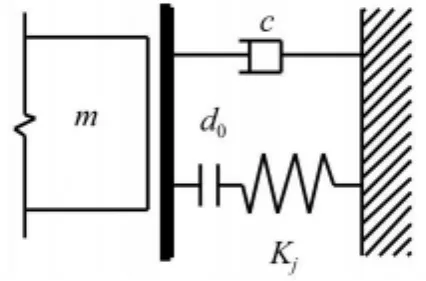
图2 接触单元模型Fig.2 Pounding model

上式中，d0为接触单元的初始间隙，此为梁体与挡块间的横向间距;yr为地震作用下主梁与墩顶间的相对位移;kimp为接触刚度，对于接触刚度的取值问题目前并没有令人完全信服的理论和方法，试验依据也不充分，本文对于桥例所采用的钢挡块的碰撞刚度取其加劲肋刚度之和。碰撞过程中的能量损失可根据阻尼耗能原理等效，阻尼的大小与碰撞过程中的恢复系数e有关，本文不考虑碰撞过程中的能量损失，即假定e=1［7］。

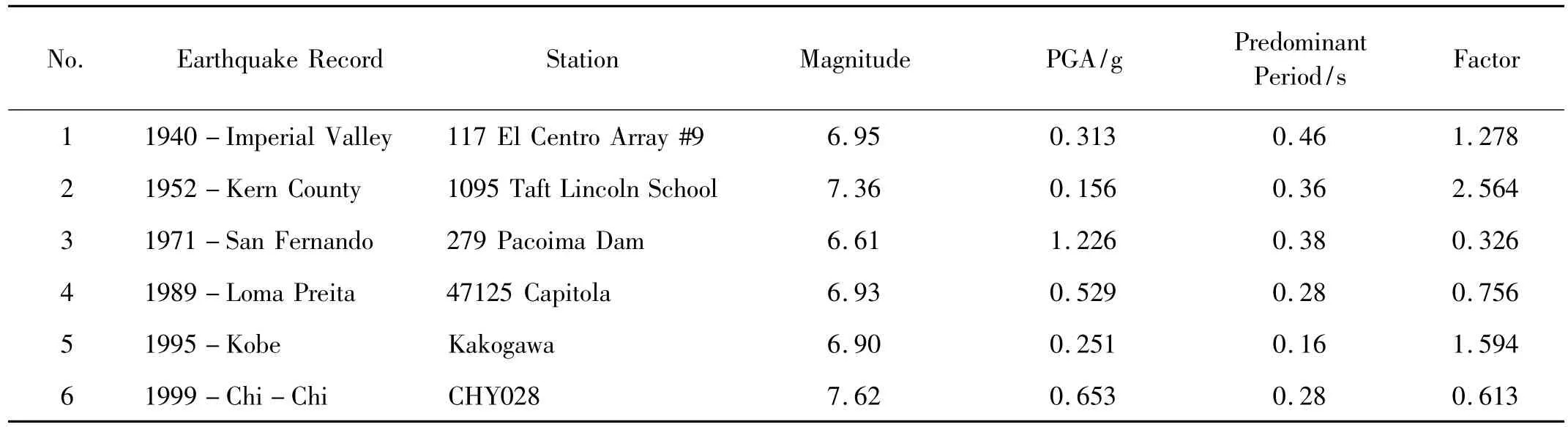
表1 加速度时程波Tab.1 The selected free-field ground motions

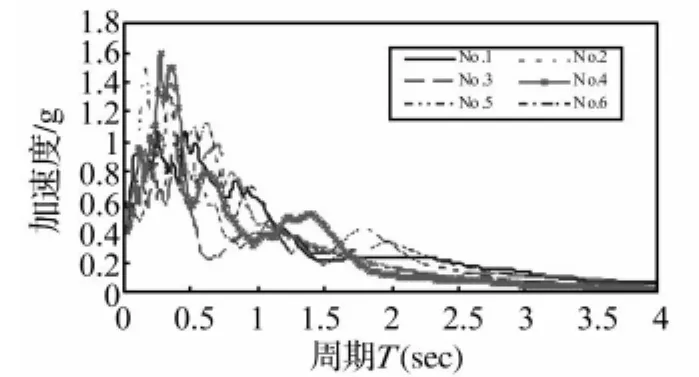
图3 地震波对应的加速度反应谱(已调幅)Fig.3 Acceleration response spectra corresponding to the selected time histories

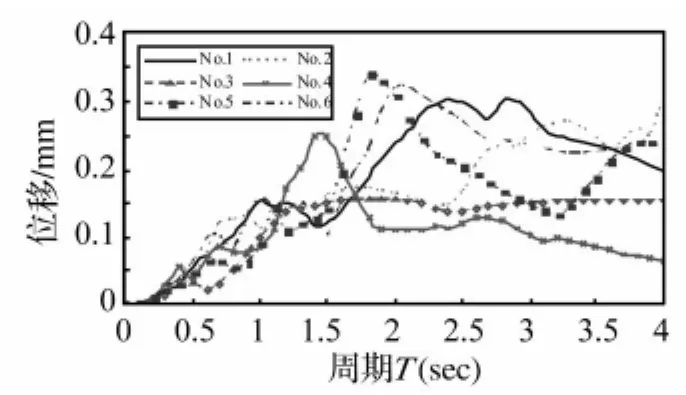
图4 地震波对应的位移反应谱(已调幅)Fig.4 Displacement response spectra corresponding to the selected time histories

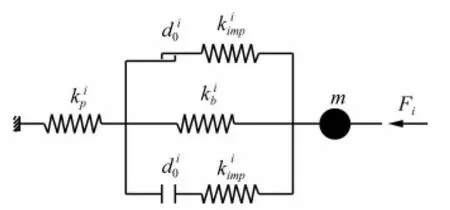
图5 等效刚度模型Fig.5 Equivalent stiffness model

1.3 地震动输入

为获得桥梁结构的动力响应，对分析模型输入横桥向的实际地震加速度时程波进行线性和非线性的时程分析。本文选用的6条地表加速度时程波(见表1)均取自太平洋地震工程中心(Pacific Earthquake Engineering Research Center，PEER)地震波数据库(PEER Strong Motion Database)。假定桥梁位于地震烈度9度区，故将每条地震波的加速度峰值调整为0.4 g。图3和图4显示的是经过调幅以后的6条时程波对应的加速度反应谱和位移反应谱。

1.4 碰撞效应分析参数

地震作用下，对于连续梁桥而言，其横桥向的传力途径大致可以描述为主梁的横向惯性力通过支座以及挡块传递给墩柱，再由墩柱传递给基础结构，最后由基础结构分散到地基。假设主梁为刚性梁，且仅考虑墩柱的弹性状态，则由墩柱、支座以及挡块组成的系统可以简化为如图5所示的等效刚度模型。

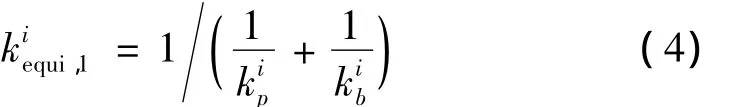
当主梁与桥墩的相对位移yir＞d0i时，则有:

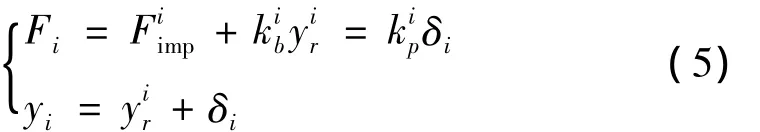
由以上关系可以导出:

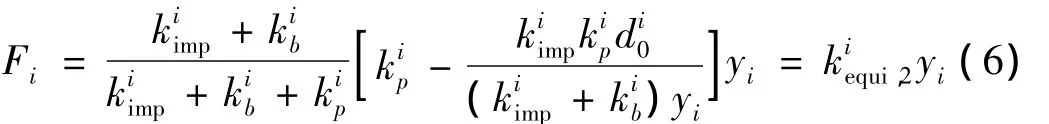
1.5 梁墩刚度比

对公式(3)和(6)的有关推导，采用了刚性梁的假定。为考察主梁的横向刚度对地震惯性力分配的影响，本文引入梁墩的横向刚度比，并对RI进行参数分析。

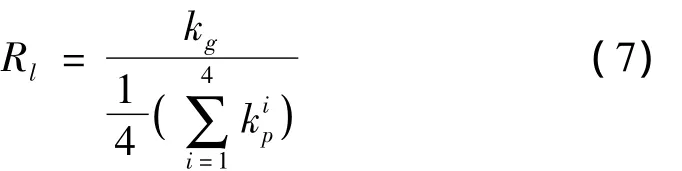
其中，kg为主梁横向刚度，kg=48EgIg/L3，L为主梁的全长。

1.6 模型的比较研究

在实际桥梁工程抗震设计时，对于上部结构与下部结构横桥向的连接处理上，通常的做法都采取固结的方式，包括《公路桥梁抗震设计细则》(JTG/T B02－01—2008)中，关于采用板式橡胶支座且横向设置限位装置的规则梁桥横向地震力的计算也按横向固结方式来处理［9］。因此，为了比较考虑碰撞效应后墩柱横桥地震力分配的变化，本文分别建立横向固结模型、横向不考虑碰撞效应的支座模型以及考虑碰撞效应的支座模型进行分析。

2 分析结果

采用结构分析软件SAP2000建立多自由度动力分析有限元模型，在横桥向分别输入表1所列举的6条时程波，进行线性和非线性时程分析，其中非线性时程分析中主要考虑的非线性因素为碰撞(即模型中的接触单元)，分析方法采用非线性直接积分法，积分步长随时程波的不同略有差异，取值为0.005 s和0.01 s两种。分析模型中，初始间隙取3 cm，各墩处初始接触刚度均取5×104kN/m。

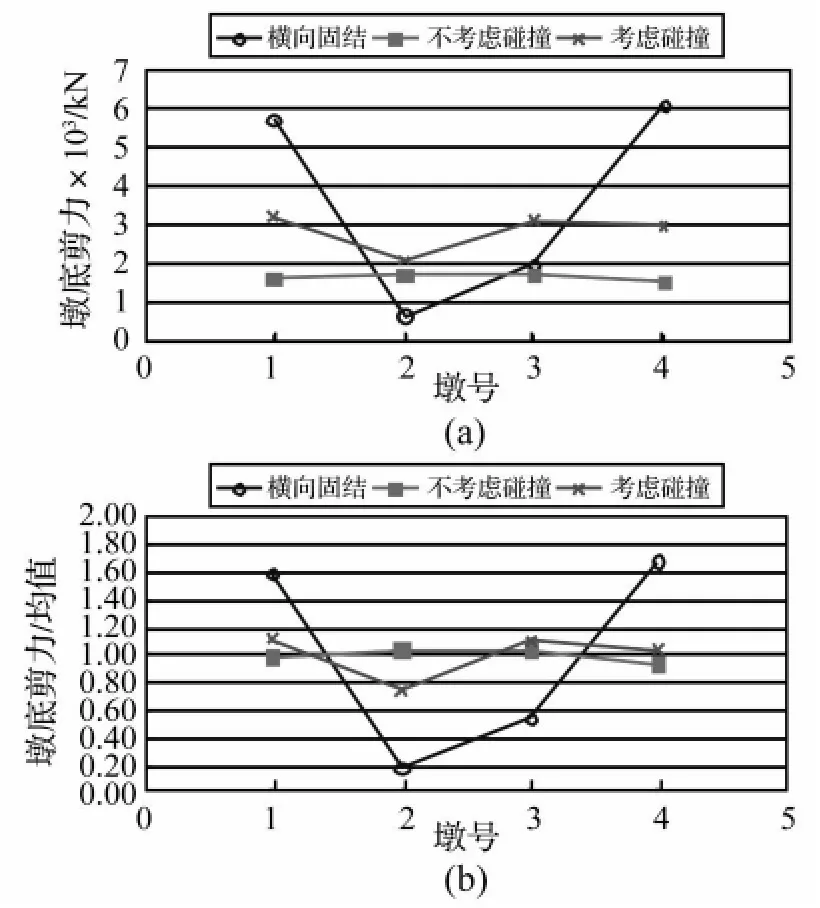
图6 各桥墩墩底横向剪力分布图Fig.6 Distribution of transverse inertial force among the piers

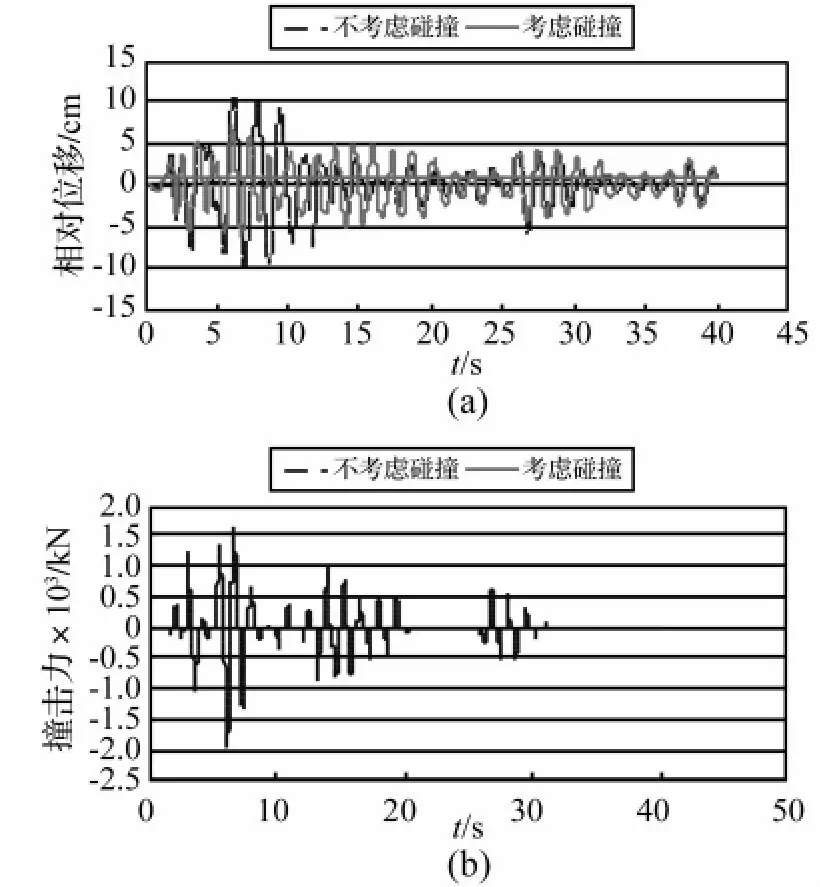
图7 1#墩梁墩相对位移和碰撞力时程曲线Fig.7 Time history of relative displacement and pounding force(Pier 1)

图6反映了各个桥墩横向地震力分布情况，其结果为6条时程波的平均，其中(b)中纵轴的墩底剪力/均值指的是每一个墩的墩底剪力与四个墩的墩底剪力平均值的比值，下同。图7表示1#墩墩梁相对位移和碰撞力的时程曲线，为地震波No.1的结果。

从图6可以清晰地发现，非规则梁桥的横向固结方式将导致主梁的惯性力分布极度不均匀，1#和4#两个最矮的墩分担了其中的大部分。对于采用同样截面的四个墩来说，抗震设计的结果不是导致中间墩的过度保守，就是引起两个边墩的剪切破坏。采用板式橡胶支座以后，各墩的受力基本趋于相等，这对于抗震设计来说是理想情况，但从图7(a)可以看到，桥墩处的梁墩相对位移非常大，其最大值达到了近11cm，累计结果更大。过大的相对位移不仅容易导致支座失效，严重的甚至引起横向落梁。从图6和图7中可以看出，挡块的设置确实使得梁墩相对位移明显减小，但各墩的墩底剪力又开始趋于不均，而且由于梁体与挡块间的碰撞而产生的撞击力使各墩分担的地震力明显增大。

2.1 地震波频谱特性的影响

图8表示的是在6条地震波输入下，各桥墩墩底横向剪力的分布情况。从图中可看出，尽管桥梁结构对不同地震动输入下的地震响应大小略有迥异，如2#墩处的响应最大差别可达70%，但对于某一座特定的梁桥而言其影响规律基本一致。就本桥例而言，相比于不考虑碰撞的情况，6条地震波都使2#墩的响应变小，3#墩的响应变大，而两个边墩则基本维持均值水平。因此，以下均从6条时程波的均值探讨碰撞效应对非规则梁桥主梁横向惯性力分配的影响。

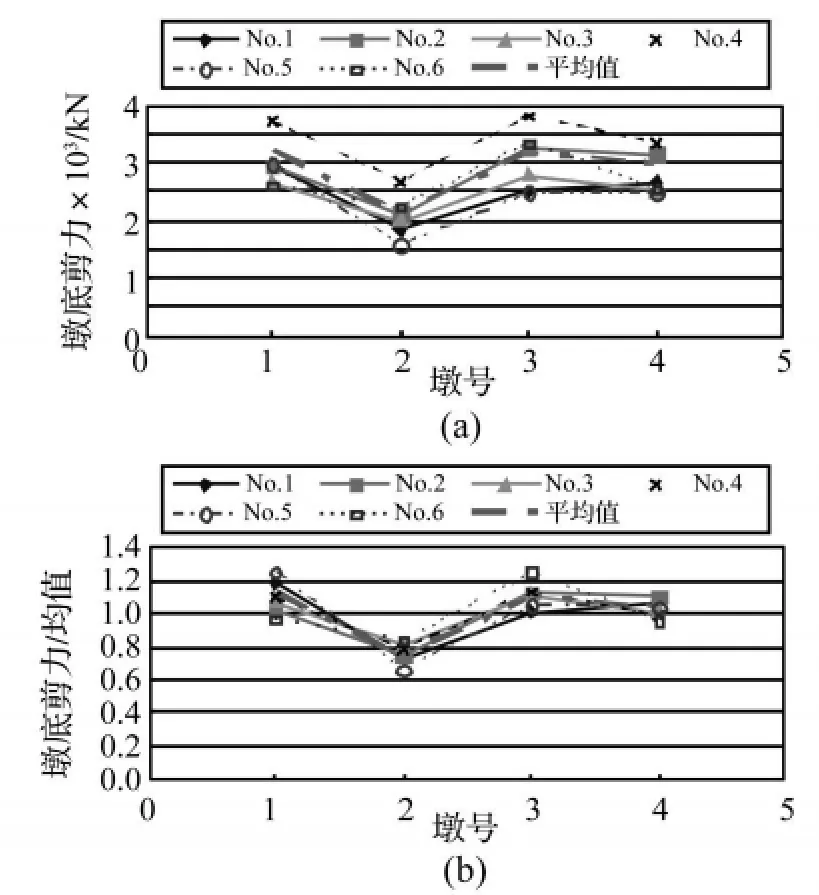
图8 地震波频谱特性对横向惯性力分配的影响Fig.8 Effects of the frequency content of the ground motion on distribution of inertial force among the piers

2.2 接触刚度的影响

从式(6)可以看到，接触刚度是影响上部结构横向惯性力分配的重要因素之一，对于钢挡块可以通过改变其加劲肋的数量来调整接触刚度。现将接触刚度分别取为 k1、k2、k3、k4，其值分别对应 5 ×103kN/m、5 ×104kN/m、5×105kN/m、5×106kN/m。进行非线性时程分析后，从图9可以看出，接触刚度对非规则梁桥上部结构横向惯性力的分配影响非常大。刚度很小时，各墩横向剪力非常接近，而刚度的急剧增加会导致各墩剪力的不均匀性显著增加。从接触单元的本质来看，这是由于接触刚度直接决定了撞击力的大小，接触刚度的增大，无疑会使碰撞效应被放大，而非规则梁桥各墩的高度和刚度等差异导致每一个桥墩处主梁与挡块间的碰撞程度互不相同，从而造成各墩对主梁横向惯性力分担的参差不齐。

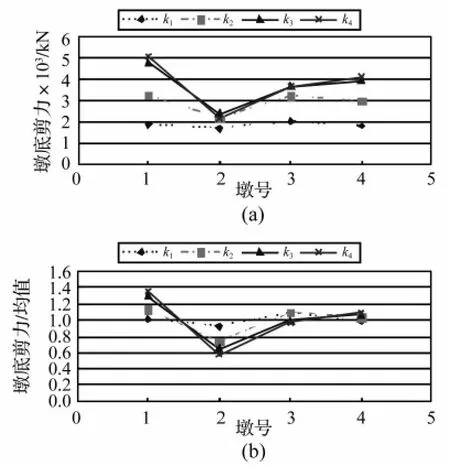
图9 接触刚度对横向惯性力分配的影响Fig.9 Effect of the pounding spring stiffness on distribution of inertial force among the piers

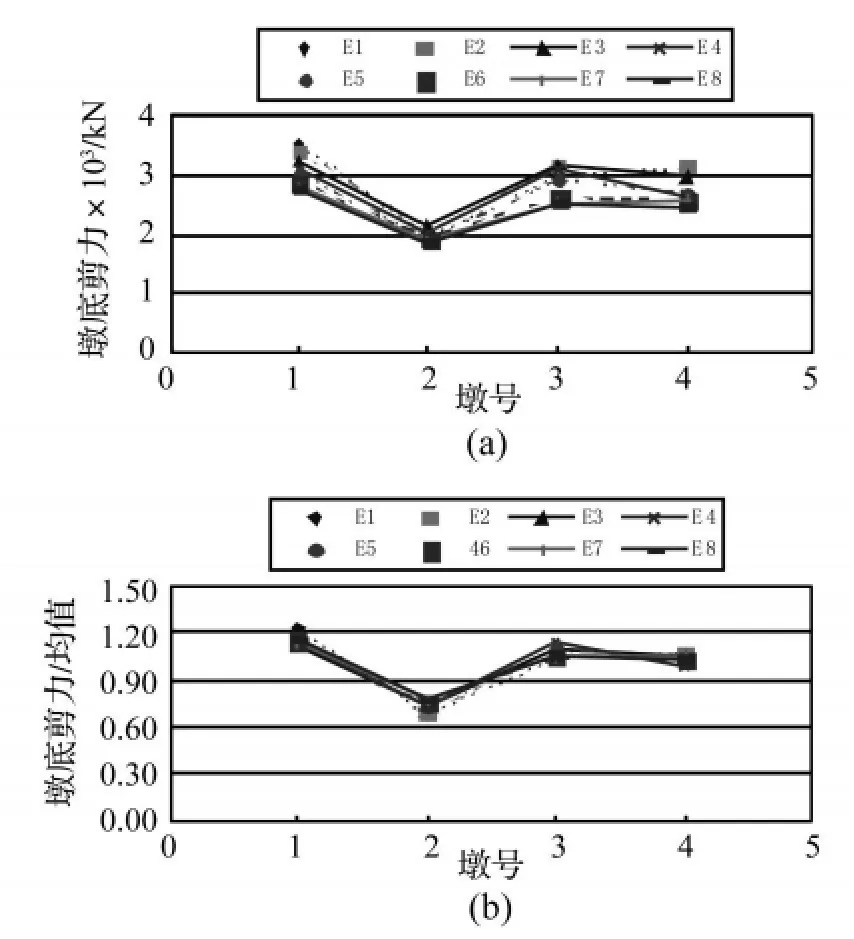
图10 初始间隙对横向惯性力分配的影响Fig.10 Effect of the gap distance on distribution of inertial force among the piers

2.3 初始间隙的影响

初始间隙的大小决定了主梁与挡块间的碰撞程度。由式(6)知，各墩处梁体与挡块的间隙影响着上部结构的横向惯性力分配，假设各墩处的初始间隙均相同，并分别取1 cm、2 cm、3 cm、4 cm、5 cm、6 cm、7 cm、8 cm，进行非线性时程分析。从分析的结果看，初始间隙对各墩地震响应的大小有较明显的影响，间隙越大，各个桥墩墩底的剪力越小;但其对上部结构横向惯性力分配的均匀性影响很小，因此单从改善非规则梁桥横向受力均匀性的角度来讲，当各墩处的初始间隙取值一致时，改变初始间隙的大小并非是一个有效的方法。

2.4 梁墩刚度比的影响

对于横向固结的连续梁桥，梁墩横向刚度比对其横向地震力的分布起控制作用［8］，而碰撞效应的考虑无疑使主梁横向刚度的影响变得复杂。显然，主梁的横向刚度不仅影响横向惯性力的分配而且也影响着碰撞效应的大小。分别对梁墩横向刚度比RI取值0.12、0.34、0.75、1.20、1.75、3、4.5、6(记为 Rl～8)进行非线性时程分析。从图11可以发现，考虑碰撞效应以后，梁墩刚度比的变化对横向惯性力分配的影响没有表现出像横向固结的梁桥那样明显的规律性，这也说明了主梁侧向刚度同时影响着碰撞发生的程度。图11总体上显示出梁墩刚度比在小值或大值范围内横向惯性力的分配更趋平均。

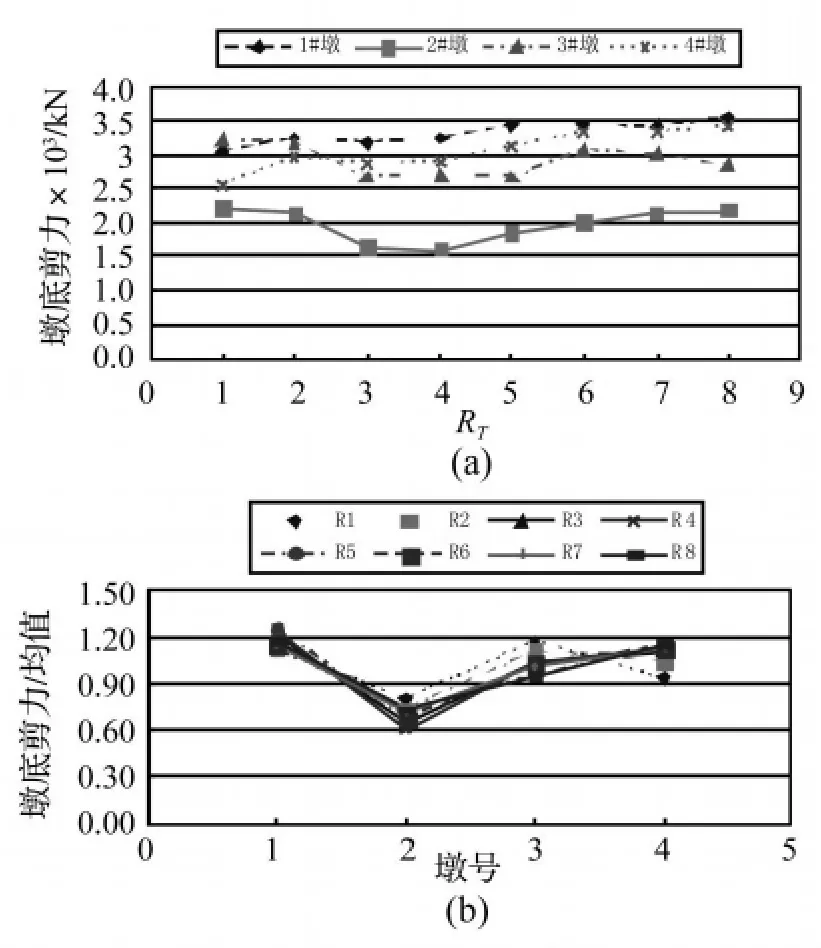
图11 梁墩刚度比对横向惯性力分配的影响Fig.11 Effect of the stiffness ratio between girder and pier on distribution of inertial force among the piers

3 结论

以往的桥梁震害和国内外的研究表明忽略梁体与限位装置间的碰撞效应会造成灾难性的后果，尤其是对地震敏感的非规则梁桥。本文正是基于这种认识初步探讨了碰撞效应对非规则梁桥各墩横向地震力分配规律的影响，最后得到了如下结论:

(1)非规则梁桥采取横向固结的方式进行设计显然不是合理的选择，这是因为横向固结不仅会增加结构的地震响应(横向固结使横向控制阵型的周期显著变短)，而且导致主梁惯性力分配的不均匀。从本文的桥例来看，横向固结模型与橡胶支座模型的横向总惯性力比值为2.17，且横向固结使得剪力最大的4#墩与最小的2#墩之间的比值达到9.0，而且四个墩差异巨大，这无疑增添了设计难度。

(2)板式橡胶支座的使用可以有效改善非规则梁桥的横向抗震性能。本文支座模型中的各墩之间剪力的最大比值相比固结模型由9.0降为1.1，四个墩几乎相等;但为限制因采用橡胶支座而导致的梁体过大的侧向位移所设置的限位装置如挡块会引起各墩地震力分布的再次不平均。

(3)由等效刚度模型可知，接触单元的接触刚度，主梁与挡块间的初始间隙对非规则连续梁桥横向惯性力分配均会产生影响。通过参数分析发现:接触刚度对惯性力分配的影响非常大，且刚度越大，惯性力分配越不均匀;而初始间隙虽然会影响结构的地震响应大小，但对惯性力的分布规律影响不大。

(4)为改善不等墩高的非规则连续梁桥横向的抗震性能，可以从梁体与挡块的接触刚度入手。本文中，在接触刚度由5×103kN/m变化到5×106kN/m过程里，四个墩的平均剪力由1810 kN增加到3719 kN，且最大与最小的比值由1.2递增至2.4，显然设法降低梁体与挡块间的碰撞刚度是改善非规则梁桥横向抗震性能的有效方法。

(5)从改善受力角度而言，初始间隙的增大会使碰撞效应减弱且不会显著改变横向惯性力的分配规律，但为了保护橡胶支座免遭剪坏，初始间隙需要进行仔细的考究和平衡。

(6)考虑碰撞效应以后，梁墩刚度比的影响更为复杂。参数分析表明，梁墩刚度比的变化对横向惯性力分配的影响没有明显的规律性。因此，为改善横向受力，梁墩刚度比并非合理的出发点。

［1］Priestley M J N，Seible F，Calvi G M.Seismic Design and Retrofit of Bridges［M］.New York:John Wiley ＆ Sons，Inc，1996.

［2］李建中，范立础.非规则梁桥纵桥向地震反应及碰撞效应［J］.土木工程学报，2005，38(1):54 －59.

［3］王军文，李建中，范立础.非规则梁桥伸缩缝处的碰撞对地震反应的影响［J］.土木工程学报，2006，39(1):84－90.

［4］邓育林，彭天波，李建中.地震作用下桥梁结构横向碰撞模型及参数分析［J］.振动与冲击，2007，26(9):104－107.

［5］Maleki S.Effect of side retainers on seismic response of bridges with elastomeric bearings［J］.Journal of Bridge Engineering，2004，9(1):95 －100.

［6］Dimitrakopoulos E，Makris N，Kappos A J. Dimensional analysis of the earthquake-induced pounding between adjacent structures［J］. Earthquake Engineering and Structural Dynamics，2009，38:867 －886.

［7］Jankowski R，Wilde K，Fujino Y.Reduction of pounding effects in elevated bridges during earthquakes［J］. Earthquake Engineering and Structural Dynamics，2000，29:195 －212.

［8］陈 亮，李建中，张文学.梁墩刚度分布对连续梁桥横桥向规则性的影响［J］.同济大学学报(自然科学版)，2007，35(9):1175－1180.

［9］中华人民共和国交通运输部.公路桥梁抗震设计细则(JTG/T B02－01—2008)［M］.北京:人民交通出版社，2008.