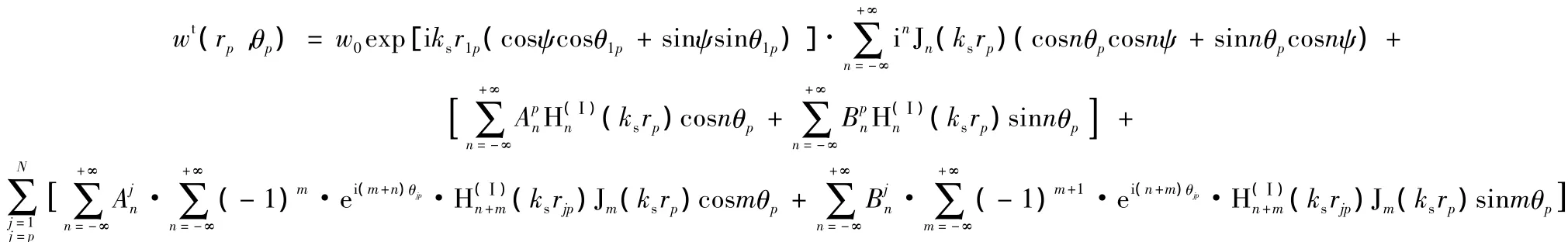SV波入射下多重散射问题的改进算法以及双排非连续刚性屏障的隔振研究
夏唐代,陈 晨,孙苗苗
(1.浙江大学 软弱土与环境土工教育部重点实验室,杭州 310058;2.浙江大学 岩土工程研究所,杭州 310058)
入射波关于多个异质体(包括孔洞)散射问题的研究由来已久。此问题最初由声学和电磁学引入,并逐渐发展到弹性波的领域[1~3]。关于弹性波的多重散射问题的研究可采用数值方法和解析方法。其中数值方法包括了边界元法和有限元法等等,解析法则是指波函数展开法等。数值方法的特点是可以应用于任意形状的多个异质体的散射问题分析,而解析法则更能抓住问题的本质,并且还可以定性地检验数值方法的准确性。
实际工程中的屏障隔振问题按照屏障本身的几何特性可以分为连续屏障隔振和非连续屏障隔振。尽管连续屏障(开口沟渠,混凝土墙等)[4]的隔振效果较理想,但对于低频人工振源以及软土、高地下水位地区,连续屏障较难施工且隔离效果较差;相反,非连续屏障具有施工方便、造价低等诸多优点。非连续屏障体系的隔振本质上便是弹性波关于多个异质体的多重散射问题。20世纪70年代初,Pao和Mow[1]采用波函数展开法首创性地研究了无限空间中单个孔洞在弹性波入射下的散射及动应力集中问题。随后,Aviles、高广运等学者[5~7]运用波动理论,得出了均质弹性土体中刚性、弹性单排实心桩对弹性波隔离的精确解。徐平[8~9]运用波函数法推导了单排弹性和刚性空心管桩以及实心桩屏障对平面弹性波的隔离效果。
然而,值得指出的是,到目前为止,关于非连续屏障的隔振问题,运用解析解法时所研究的对象均是在一条直线上,理论公式的推导都是建立在单排桩上,且不能推广到多排桩,而关于任意分布的多个圆柱体对于弹性波的多重散射解析解问题至今仍未见报道。考虑到实际工程中常常采用多排桩隔振(尤其是在软土地区和高地下水位地区),同时桩采用梅花型布置以增强隔振系统的整体刚度及隔振效果,使得多排桩的散射隔振研究成为一个亟待解决的问题。
如果刚性桩埋置足够深,则其对人工振动产生的弹性波的散射可以简化为固定刚性异质体对弹性波的散射问题,因而本文首先以无限均质弹性空间中任意分布的N根固定刚性桩在弹性波入射下的模型为例,阐述了本文关于多重散射的改进计算方法,推导了散射系数的计算公式。该改进方法运用范围广,必要时可直接退化为研究单排非连续屏障隔振体系。接着,取双排刚性桩隔振的模型,采用本文所提出的算法研究了双排固定刚性桩关于SV波(偏振方向与桩体轴线一致)[7]的隔离效果,为工程上常用的多排桩隔振问题的分析提供新的研究思路。
1 波函数展开
如图1所示,取任意分布的N根固定刚性桩位于各向同性的无限均质弹性土体中。桩的半径为al(1≤l≤N,N为桩的数目),平面SV波的入射角为ψ。考虑到问题的实质是多个圆柱体对于弹性波的散射问题,因而在计算分析时采用一组圆柱坐标系统。其中,任意点s相对于j桩圆柱坐标系的坐标为(rj,θj),相对于p桩圆柱坐标系的坐标为(rp,θp)。任意圆柱坐标系(rp,θp)的原点相对于另一个圆柱坐标系(rj,θj)的原点的距离为 rjp,角度为 θjp。
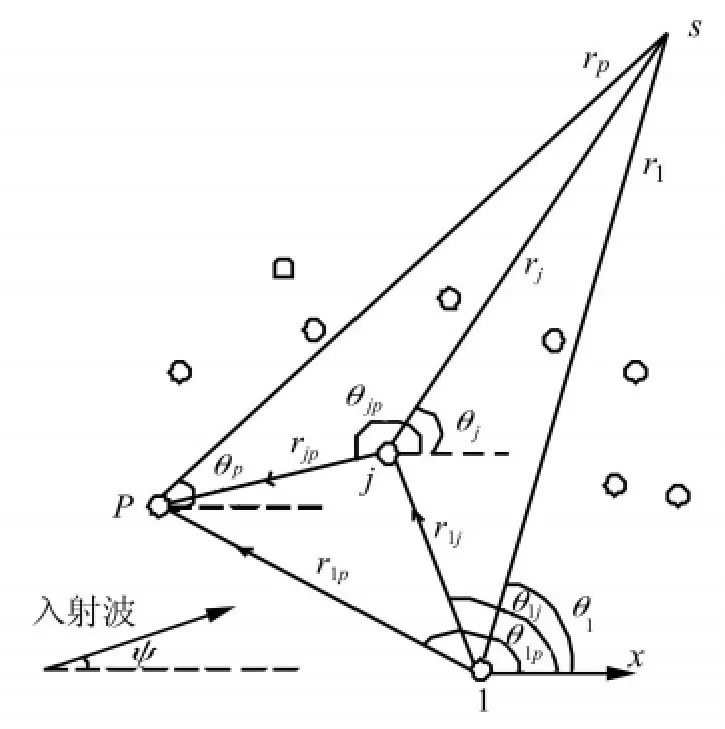
图1 任意N根固定刚性桩对弹性波的散射Fig.1 Scattering of elastic waves by an arbitrary configuration of fixed rigid piles
SV波的偏振方向与桩体轴线一致,在波的传播过程中不会与其他体波(P波,SH波等)产生耦合散射,故在分析问题时,只需求解标量的波动方程。另外,考虑桩体的埋置足够深,因而此处的多重散射问题可以简化为二维平面问题来研究。
偏振方向与桩身轴线一致的SV平面简谐体波应当满足Helmholtz方程:
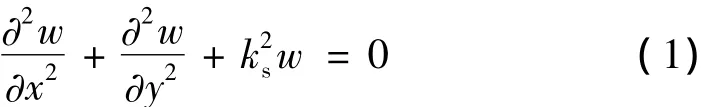
式中,ks=ω/c为土体中SV波的波数;ω为圆频率;c为土中的波速。
取入射SV波的幅值为w0,则在参考坐标系xpoyp下,满足上述方程的入射SV波可以表示为如下的Fourier-Bessel函数的级数形式:
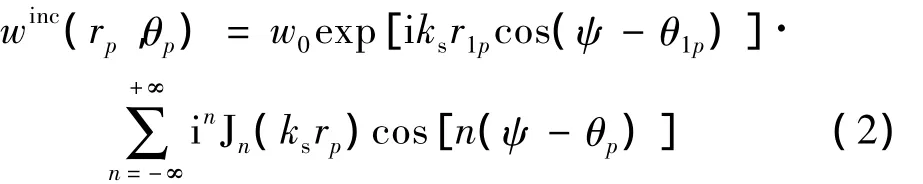
其中,上标inc表示入射波;Jn(·)为n阶第一类贝塞尔函数;i为虚数单位为了研究的方便,上式及以下的讨论中均略去了时间因子e-iωt。
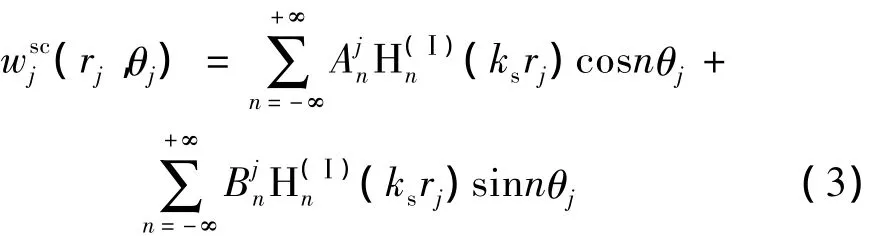
由于每根桩均会对入射波散射,且相应的散射波场均依附于自身的圆柱坐标系统。于是,总的波场可以表示为入射波场和散射波场的叠加:
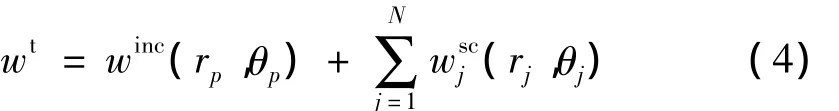
式中,上标t表示总波场。
(2)教学文件齐备,但大纲的执行情况较差,难以保证教学内容的系统性,教学管理部门应加强监督力度,进一步规范管理。
运用更具一般意义上的Graf加法定理[10],可以把坐标系(rj,θj)下的散射位移场转换为坐标系(rp,θp)下的形式,若 j≠p,则有,
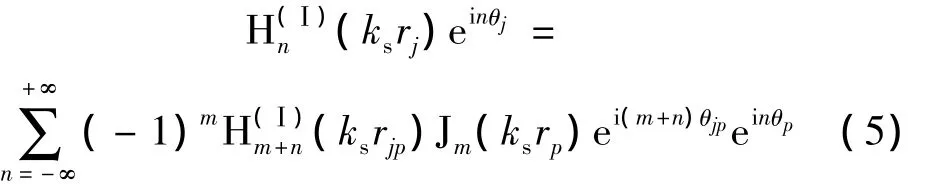
将式(2)、式(3)、式(5)式代入到式(4)中,便得到坐标系(rp,θp)下的总波场表达式(限于篇幅,表达式见附录)。
2 散射系数的求解
由于考虑了桩体为固定且刚性的,假定土体与刚性桩体在界面处完全联结,即桩体与周围土体在界面处位移连续,因而对于任意p桩而言,边界条件为:
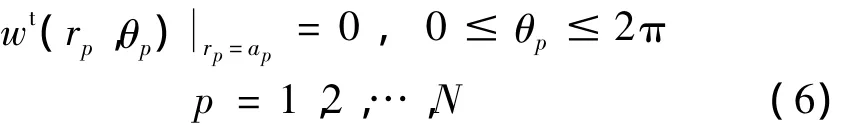
将式(2)、式(3)、式(4)、式(5)代入到式(6)中,根据不同阶的三角函数sinnθj和cosnθj线性无关的性质,经过化简,最终可得关于平面SV波入射下散射复系数和的两个无穷线性方程组:
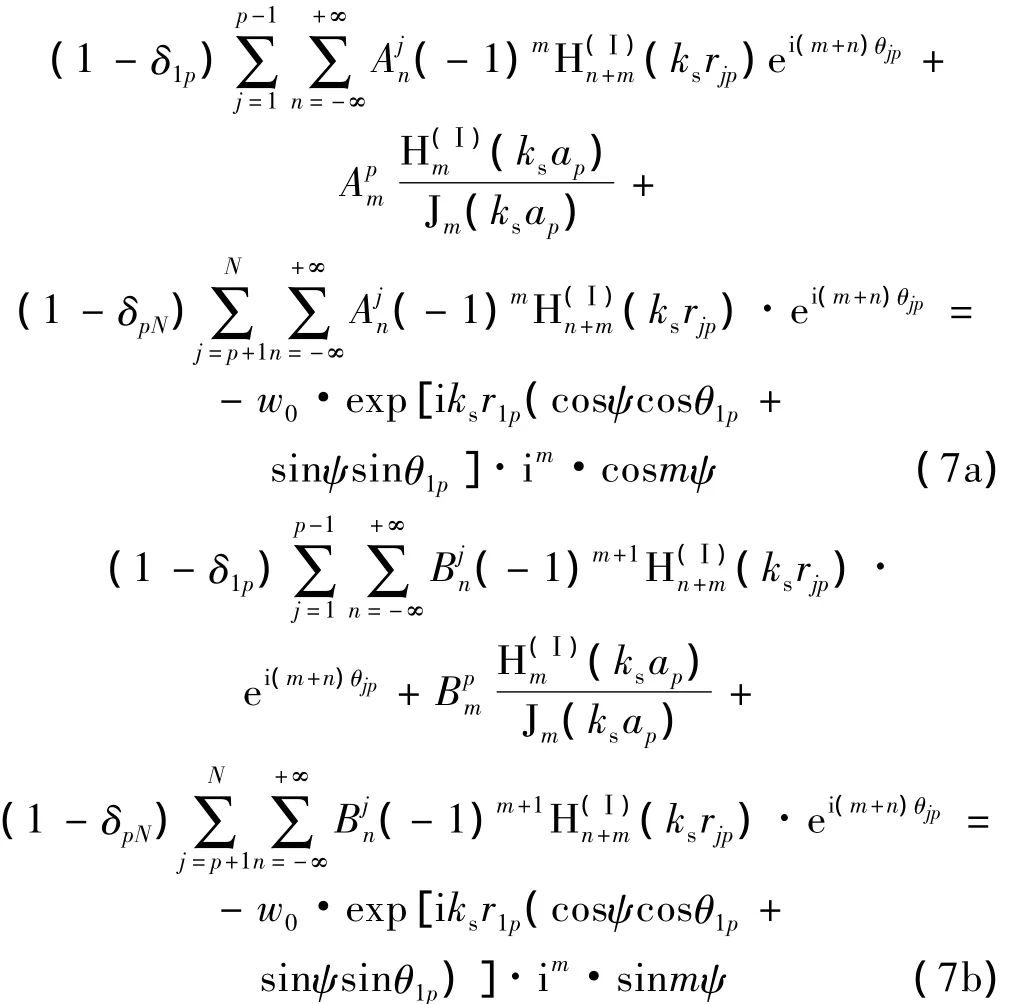
式中,m= -∞,…,-2,-1,0,1,2,…,∞, 1≤p≤N解出散射系数后,便可以得出整个波场。
3 数值计算
为了验证上述关于平面SV波入射下多重散射问题改进算法的正确性,取各根桩的分布如图2所示,则问题演变为双排固定刚性桩屏障对于SV波的隔离问题。
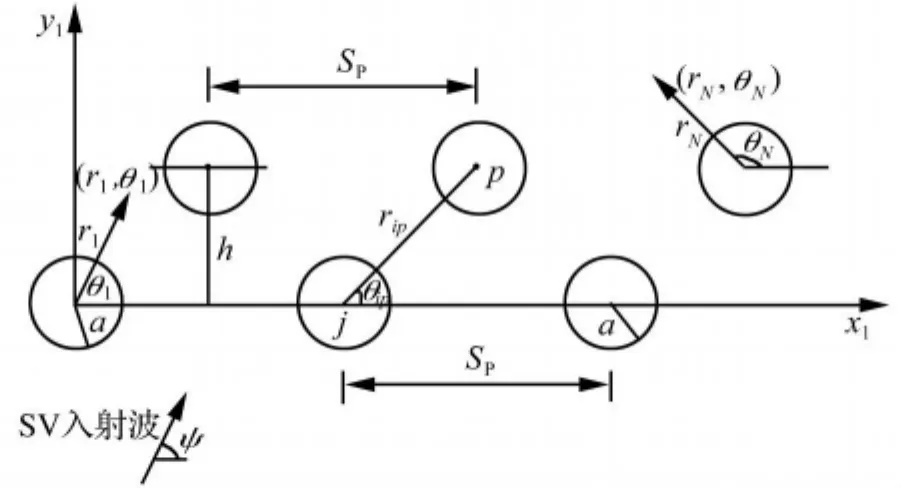
图2 双排固定刚性桩隔振模型Fig.2 Modeling of vibration isolation by rows of fixed rigid piles
设所有刚性桩的参数都一致,桩列均匀布置,取桩的数量为N=8,桩的半径均为a=1,每排之中相邻两桩之间的距离为Sp=6a,两排桩之间的间距为h,假定平面SV波垂直于屏障入射,即ψ=π/2。对入射波位移场的频率进行归一化处理:

此外,再引入SV波的透射系数TIw[12],
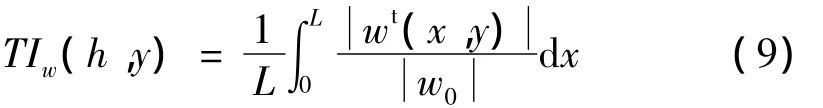
式中,L为屏障的宽度,L=Sp(N-1)/2,Sp=6a。取其他参数不变,研究了排间距h变化时屏障后y/a=150、y/a=200以及y/a=250处(此区域为最佳的隔振位置)TIw的变化,如图4所示。图4实际反映的是某固定y/a上在屏障宽度上的几何平均值,表征着屏障对于入射波能量的耗散性。
从图3可以看出,对应于不同的h,屏障的最佳隔振区域基本上都位于双排桩的中心线上,表明此时双排桩屏障可视为一个整体在发挥着作用,另外,还可以得出,屏障后的无量纲位移等值线在越靠近屏障处比较密集,梯度大,远离屏障处则较为松散,梯度小。特别地,h=0时,退化为单排桩隔振问题,此时数值计算所得结果与徐平等学者的完全一致[9]。
不过,所不同的是,图3(a)、图3(b)、图3(c)可以得出,当h从0变化到1.5a时,双排刚性桩屏障的隔振效果逐渐变好,屏障后的最佳隔振区域范围在增大,无量纲位移值整体上也在减小,由图3的(c)、(d)、(e)可以得出,随着h的继续增大,隔振效果已经逐渐开始变差,无量纲位移值增大,且h=4.5a时的屏障后最佳隔振区域上无量纲位移最小值为0.4,是h=1.5a时屏障后无量纲位移最小值0.2的两倍。另外,从图4可以看出,屏障后的透射系数随着h的变化呈现出先减小后增大的趋势,且总体上y/a越大,相应的透射系数TIw也越大,表明离屏障越远处隔振效果越差,这点同图3所得出的结论是一致的。
取h=1.5a,研究此种情况下(整体上来讲隔振效果最为理想)双排刚性桩的一些隔振性质。为了研究屏障前后的位移场,绘制了屏障中心线前后无量纲位移的变化,如图5所示。另外,绘制了双排桩屏障后不同x/a处的无量纲位移随y/a的变化曲线,如图6所示。
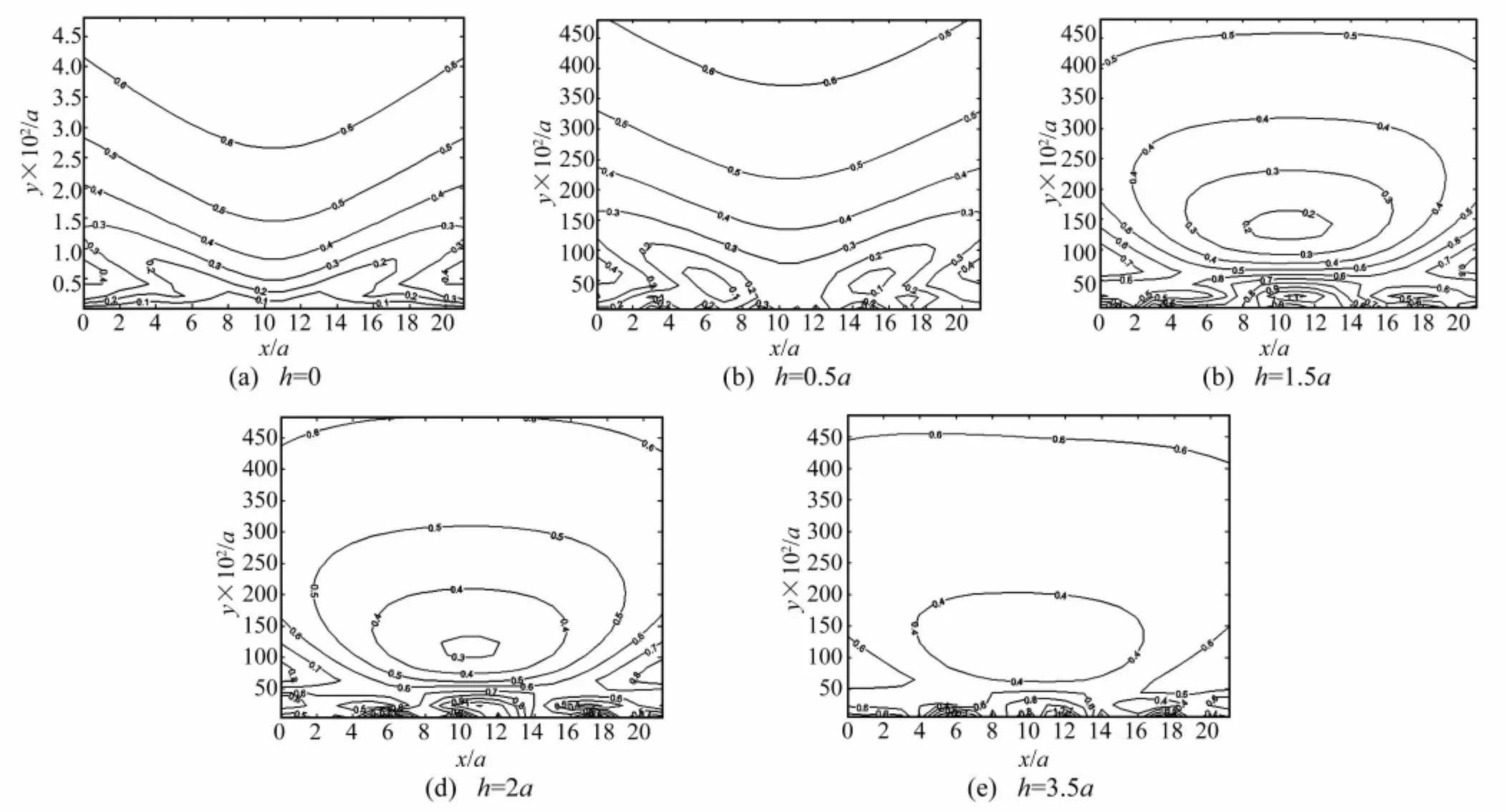
图3 屏障后无量纲位移等值线图随h的变化Fig.3 Contour of normalized displacement amplitudes behind the barrier with variation of h
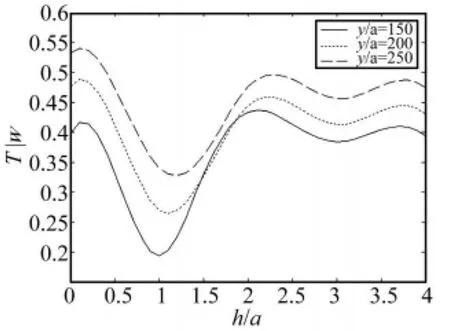
图4 屏障后的透射系数Fig.4 Transmissibility index for y/a=150,200,250
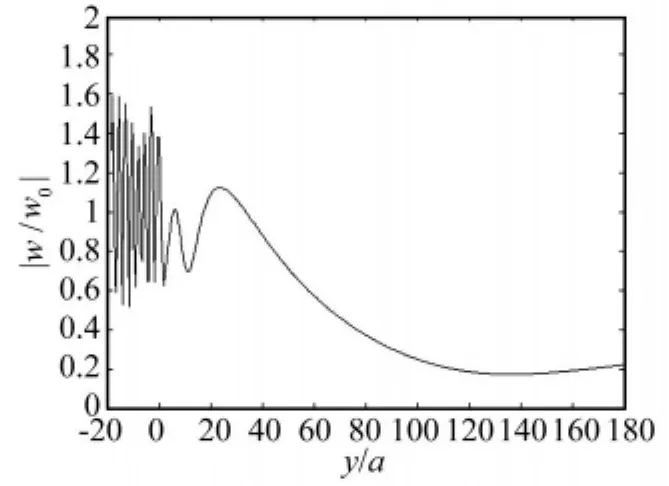
图5 屏障前后中心线上的无量纲位移Fig.5 Normalized displacement amplitudes along the center line of the barrier for h=1.5a
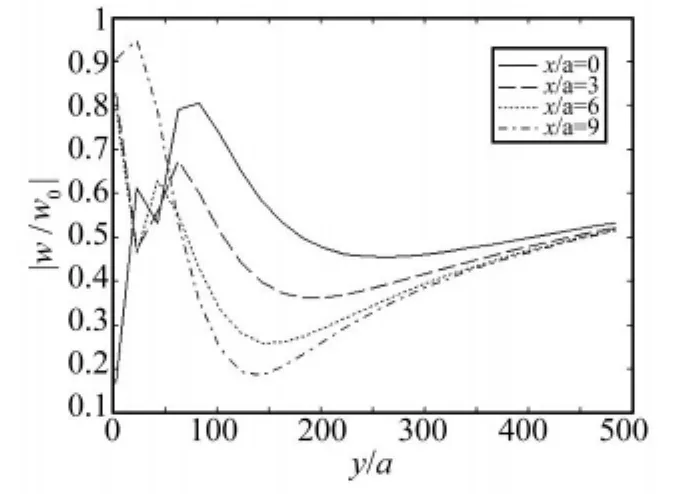
图6 屏障后不同位置处的无量纲位移Fig.6 Normalized displacement amplitudes for h=1.5a,x/a=0,3,6,9
从图5可以看出,双排桩屏障前的区域有明显的振幅放大现象,这是因为入射波与屏障的反射波发生相长干涉的缘故,而在屏障后,土体运动的振幅迅速衰减,表明此双排桩屏障起到了明显的隔振效果。这点同Aviles等学者的单排非连续屏障理论是一致的[6,7]。此外,从图6可以看出,在屏障后紧靠屏障的较小区域内(y/a<50)变化曲线较复杂,不过在离屏障较远的区域(50<y/a<500),则可以发现:在相同的y/a处,隔振的无量纲位移值都大致趋向于同一值0.53,且越靠近屏障中心,无量纲位移值越小,即隔振效果越好,这点同之前图3分析得出的结论是一致的。
4 结论
假定土体为各向同性的均质弹性土体,本文运用更为完整的Fourier-Bessel波函数展开式以及更为广义上的Graf加法定理,根据桩土位移边界条件,推导了任意分布的无限长固定刚性桩对于平面SV波的散射解析解。随后,研究了梅花型布置的双排刚性桩屏障对于弹性波的隔离问题,分析了当排间距h对于此双排刚性桩体系隔振效果的影响。特别地,当h=0时,问题退化为常见的单排非连续屏障的隔振。通过数值分析,结果表明:
(1)排间距h对于隔振效果有着重要影响。当h较小时,双排桩隔振效果随着h的增大而增强,随着h的继续增大,双排桩之间的叠加干涉效果减弱,隔振效果开始变差。最佳隔振效果为排间距h=1.5a左右。
(2)屏障中心处的隔振效果好于屏障边缘处,且双排桩屏障体系的最佳隔振区域位于距离屏障后的一定距离上。
(3)双排桩屏障与单排桩屏障一样,屏障前存在明显的振幅放大现象,而在屏障后振幅则迅速衰减。
[1]Pao Y H,Mow C C.Diffraction of elastic waves and synamic stress concentrations[M]. New York:Crane and Russak,1973.
[2]Twersky V.Multiple scattering of radiation by an arbitrary planar configuration of parallel cylinders and by two parallel cylinders[J].Journal of Applied Physics,1952,23(4):407-414.
[3]杨桂通,张善元.弹性动力学[M].北京:中国铁道出版社,1988:148-152.
[4]Woods R D.Screening of surface waves in soils[J].J.Solids Mech.and Found.Div.ASCE,1968,94(4):951-979.
[5]高广运.非连续屏障地面隔振理论与应用[D].杭州:浙江大学,1998.
[6]Aviles J,Sanchez-Sesma F.Piles as barriers for elastic waves[J]. J. Geotech. Engrg, 1983,119(9):1133-1146.
[7]Aviles J,Sanchez- Sezma F.Foundation isolation from vibrations using piles and barriers[J].J.Geotech.Engng.ASCE,1988,114(11):1854-1870.
[8]徐 平,夏唐代,周新民.单排空心管桩屏障对平面SV波的隔离效果研究[J].岩土工程学报,2007,29(1):131-136.
[9]徐 平,闫东明,邓亚虹,等.单排非连续刚性桩屏障对弹性波的隔离[J].振动与冲击,2007,26(11):133-137.
[10]Watson G N.A treatise on the theory of bessel functions[M]. CambridgeUniversityPress, London, N.W.,England,1966.
[11]Barkan D D.Dynamics of bases and foundations[M].New York:Mc Graw-Hill Book Co Inc,1962.
[12]Ahmad S,Al-Hussaini T M.Simplified design for vibration screening by open and in-filled trenches[J].J.Geotech.Engng.,1991,117(1):67 -88.
[13]Abramowitz M,Stegun I A.Handbook of mathematical functions with formulas,graphs,and mathematical tables[M].New York:Dover Publications,Inc,1970.
[14]Balendra T,Thambiratnam D P,Koh C G,et al.Dynamic response of twin circular tunnels due to incident SH waves[J].Earthquake Engineering and Structural Dynamics,1984,12:181 -201.
[15]梁建文,张 浩,Lee V W.平面P波入射下地下洞室群动应力集中问题解析解[J].岩土工程学报,2004,26(6):816-819.
附录1
总位移波场表达式: