基于预试验分析的复杂箱体结构试验模态研究
张喜清,项昌乐,刘 辉,陈福忠
(北京理工大学 车辆传动国家重点实验室,北京 100081)
模态分析是研究结构动力特性的一种近代方法,是系统辨别方法在工程振动领域中的应用。其中普遍采用的方法是数值模态分析和试验模态分析相结合来解决工程结构振动问题,试验模态分析可以获得结构的模态参数,可以利用其结果检验、补充和修正原始有限元动力模型。目前,国内外学者在模态参数识别[1][2]和试验模态分析[3,4]方面已经进行了很多研究,但在试验测点和激励点的优化方面[5]研究较少。在进行模态试验时,在已有的测试系统和参数识别方法条件下,为充分激起结构给定频率范围内尽可能多的模态频率,获得高质量的试验测量数据,结构响应测点和激励点数目、位置和方向的优化变得尤为重要,其准确与否直接影响后续工作的准确性。
本文以某型复杂变速箱箱体为研究对象,首先建立箱体的有限元模型,进行数值模态求解,并在此基础上对箱体进行预试验分析,优化响应测点数目及位置、激励点位置及方向;然后进行锤击模态试验,识别出表征箱体动力学特性的各阶模态参数,并将试验所得频响函数和模态置信判据准则(MAC)与预试验分析结果进行比较。
1 箱体预试验分析
在对箱体进行模态试验之前,需对箱体模型、材料参数等做一系列的简化,使得有限元模型与实际结构间存在一定程度的差别,因此箱体有限元模型的准确性对模态分析及预试验分析有一定的影响。但对于变速箱箱体这类复杂的结构,通过预试验分析可以对预先选取的响应点进行评价,在能够清楚地辨识各阶模态的前提下将试验模态测试点数目降到最低,大大减少试验模态测试的工作量,同时得出较为理想的激励点的位置和方向,为模态试验提供参考,指导模态试验得到较理想的模态数据,提高信噪比,保证测试精度。
1.1 箱体有限元模态分析
该变速箱箱体由上箱体、下箱体、左端盖、右端盖、前盖五部分组成,结构复杂,解析法根本无法求得其模态,因此用有限元法进行求解。对箱体各部分进行分析简化,建立其有限元模型,总计108403个实体单元,主要由六面体和楔形体单元构成,箱体有限元模型如图1,并利用Lanczos方法来求解系统的模态参数。图2为0Hz~2000Hz频率范围内结构的各阶模态频率分布,由图可知,箱体模态比较密集,共130阶模态。
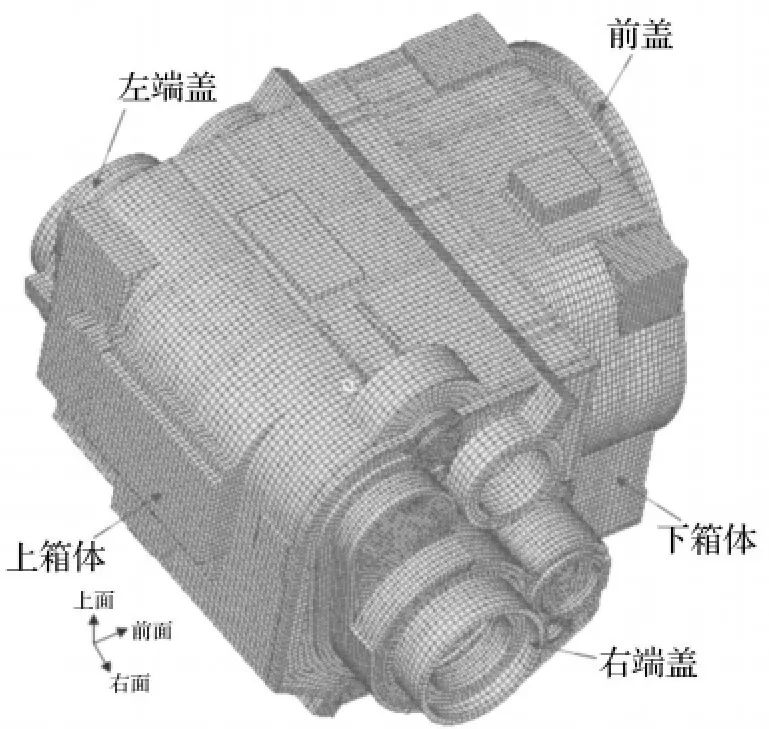
图1 箱体有限元模型Fig.1 Finite Element Model of Housing
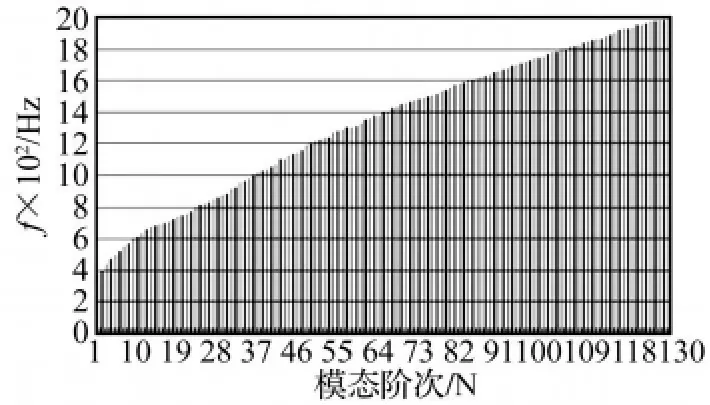
图2 箱体有限元模型各阶模态频率分布Fig.2 Frequency Distributing of Housing FEM
1.2 响应测点的选择准则
在求得箱体有限元模态结果的基础上,选定一组响应测点,易于传感器安装、对结构局部质量和刚度影响不大并能准确地区分所感兴趣的各阶模态,对所选测点对应的有限元模态振型进行模态置信判据准则(MAC)分析,检查各阶振型的相似程度,并以此判断所选测点是否合适。
MAC用来表示各阶模态振型的相关程度,MAC值在0和1范围内,第i阶模态振型向量{φ}i和第j阶模态振型向量{φ}j之间的MAC定义为[6]:
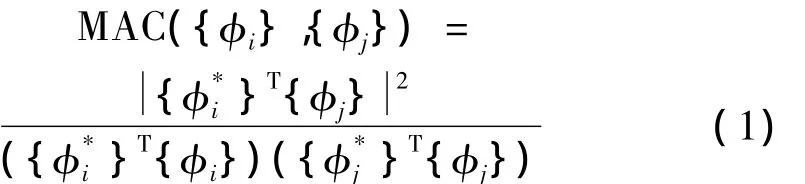
通过MAC矩阵,可以定量地阐明振型的相关程度。如{φ}i和{φ}j是同一个模态振型向量的估计,MAC接近于1(100%),即两者是线性相关的;如果是两个不同模态振型向量的估计,MAC应该接近于0,即两者是相互独立正交的。
如果非对角线上的MAC值比较大,这表明不同阶次的模态振型间存在混淆现象,用于辨识振型的自由度数目不足,此时需增加测点,直至最终所选响应点能将各阶模态清晰辨识出来。模态振型空间混淆现象多发生在大型复杂结构或组合结构的模态试验中,如果不注意,会导致后续进行试验模态振型与有限元模态振型进行MAC相关性分析时出现错误的结论。
1.3 激励点的选择准则
对激励点位置的选择,采用驱动点留数(DPR)方法[7],优化激励点位置及方向,可以激起结构更丰富的模态。
留数Aefr借助模态参数得出结构在f点激励,e点响应的频响函数表达式为:
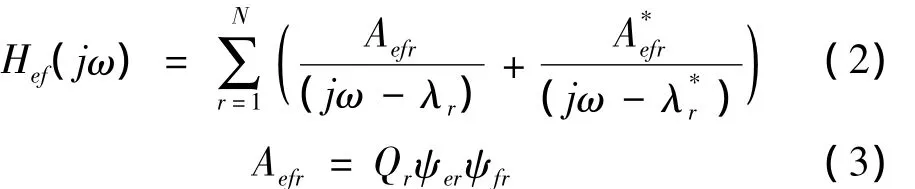
在纯模态情况下,若按单位模态质量换算,模态比例系数Qr为:

第r阶模态对于驱动点留数(e=f)为:
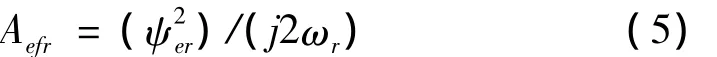
式中,ψer为第r阶模态在驱动点e自由度处的振型系数;ωr为第r模态频率。
如果某激励位置对应尽可能多的模态,其DPR值都大,这样的激励点即为比较好的激励位置。
1.4 箱体预试验分析
箱体属于较复杂的组合结构,实际模态测试时,只能在外表面进行测点布置,因此在箱体有限元模型外表面均匀选取一组数量最少,而又可以基本反映箱体结构外形的一组测点作为初始测点组,共152个测点,具体布置如图3。
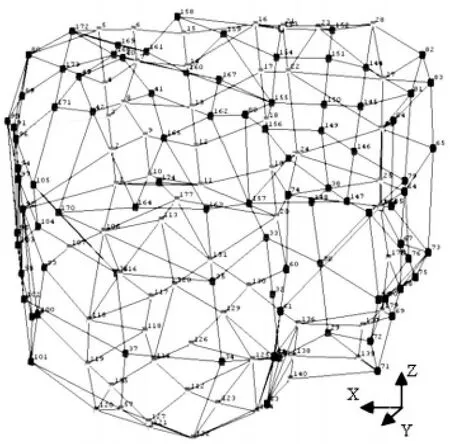
图3 箱体初始测点组分布Fig.3 Initial Measuring Points Distributing of Housing
对该箱体有限元模型进行预试验分析,频率范围为0Hz~2000Hz,利用上述基本测点组对各阶模态振型作相关性分析,得到模态置信准则(MAC)图,如图4。
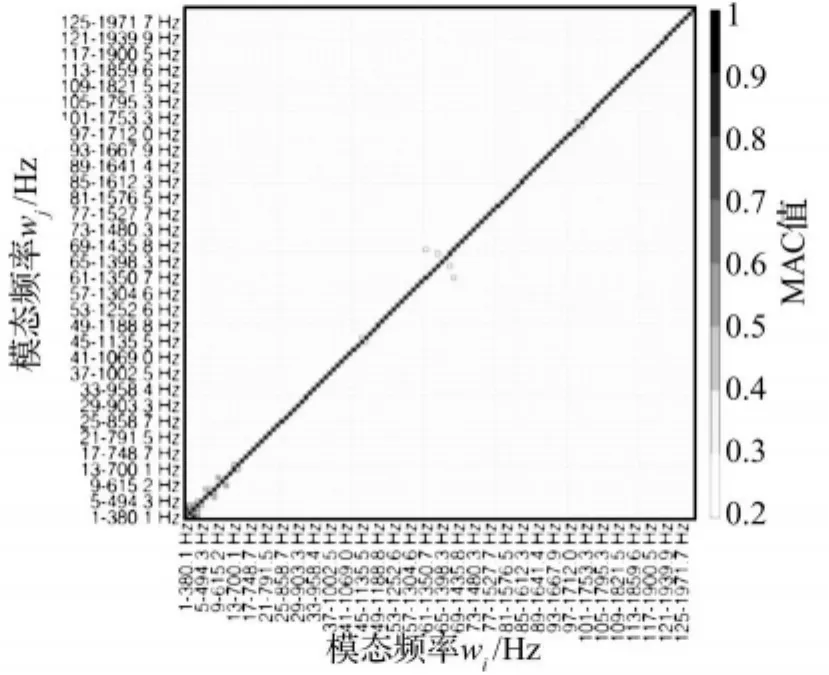
图4 初始测点MAC图Fig.4 MAC of the Initial Measuring Points
由图4可以看出,主要在低频段(380Hz~600Hz)范围内,非对角线MAC值(MODMAC)值较高,如表1所示,表明初始测点模型在不同阶模态振型间存在相关情形,该测试模型存在振型空间混淆现象。表中第2阶和第4阶模态振型MODMAC值最高为0.927,其它则在0.2~0.45范围之间,说明该测试模型存在振型空间混淆现象,需要增加响应测点来区分各阶模态振型。
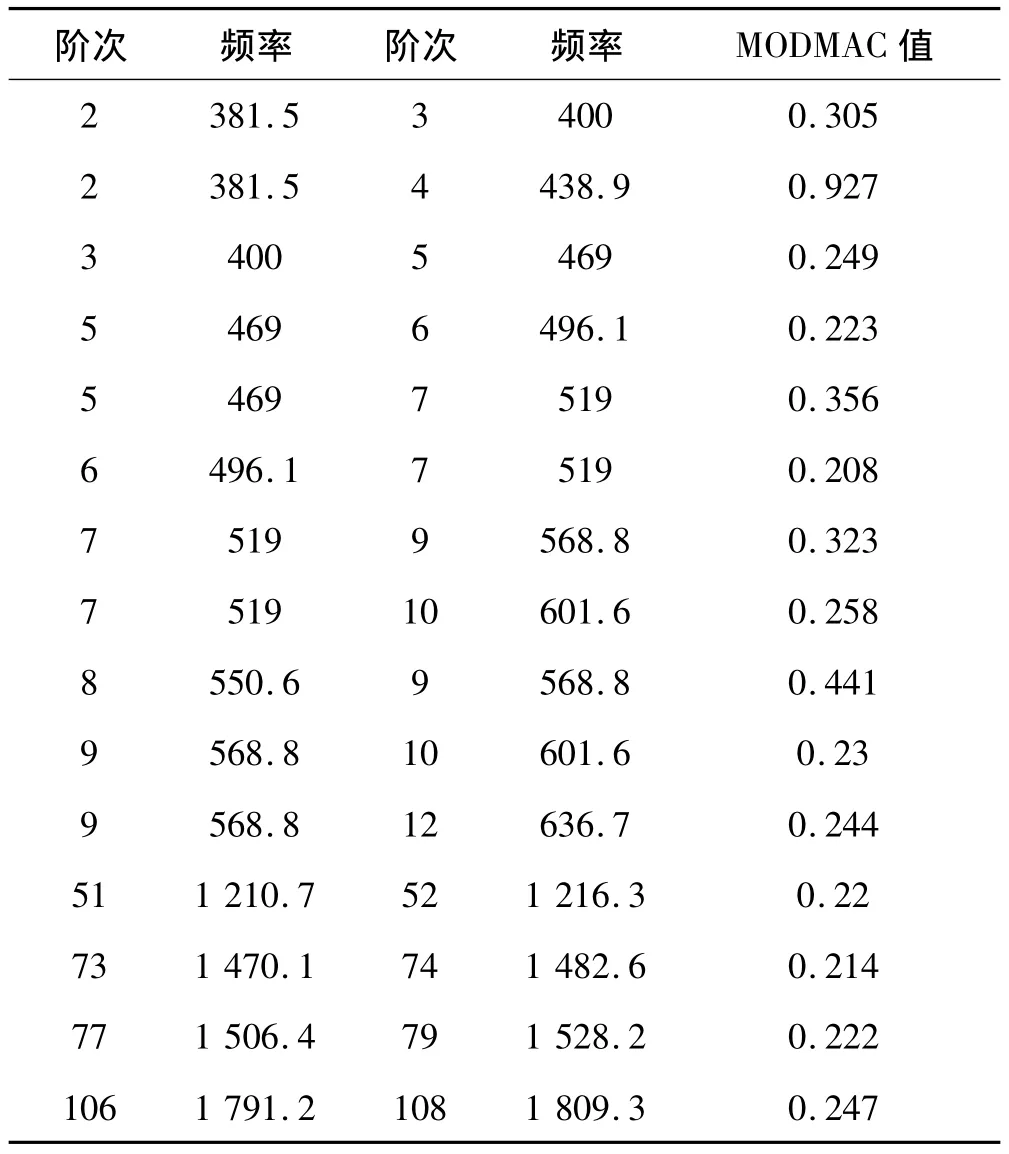
表1 初始模型非对角线MAC值Tab.1 MODMAC Value of Initial Model
由于该箱体为组合结构,试验中只能在箱体外表面布置传感器。对存在空间混淆的各组振型进一步分析,可知箱体表面初步选定的测点构成的模态振型具有相似性,振型的差异主要在于箱体内部筋板和隔板处。为了消除振型混淆现象,需在箱体内部影响各阶振型的筋板和隔板上增加测点,共增加14个测点,经分析增加测点后,模型MAC值如图5。
由图5可知,增加测点后,基本消除振型空间混淆现象,且MODMAC值都低于0.2,测点布置比较准确,由此确立箱体模态试验的测点布置方案。
对所有测点各自由度下的驱动点留数(DPR)进行计算和分析,按DPR值由大到小列举前6个不同激励位置的DPR加权平均值,如图6所示。
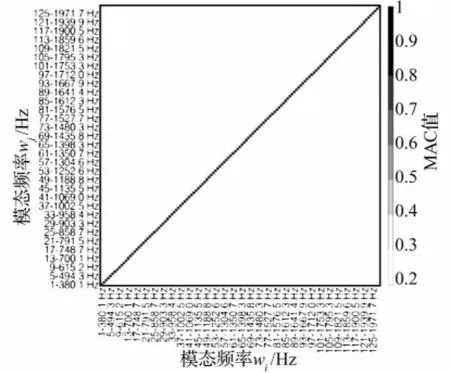
图5 增加测点后MAC图Fig.5 MAC of the Updating Measuring Points
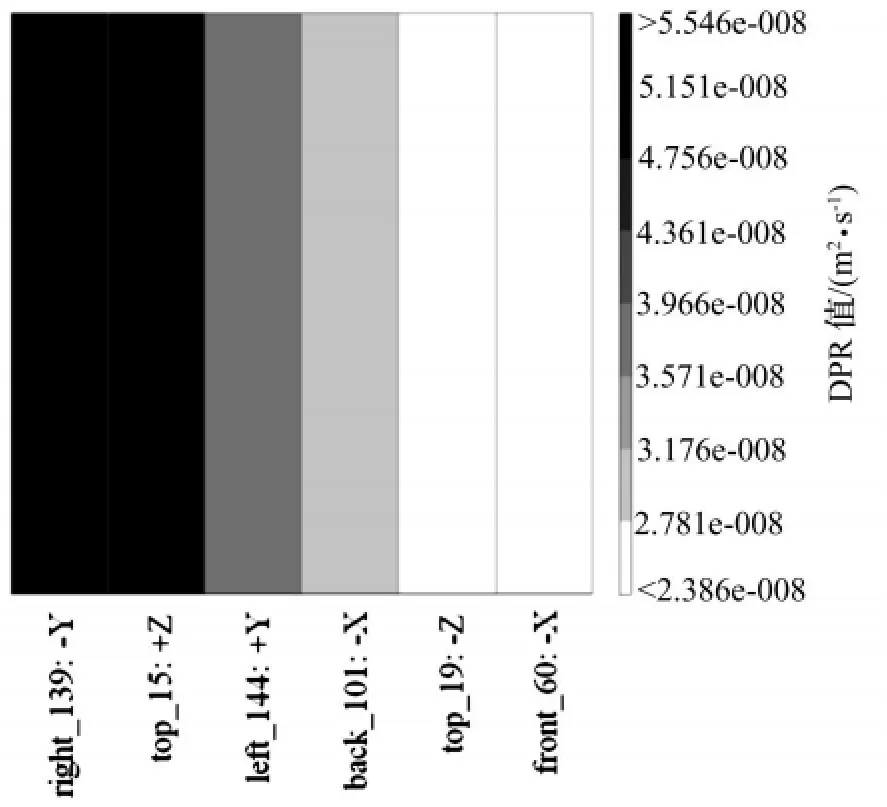
图6 测点DPR加权平均值Fig.6 DPR Weighted Average value of Measuring Points
由图6可知,箱体右侧139测点-Y方向DPR加权平均值最大,在该位置激励可以比较好的激起结构的各阶模态,由此确立箱体模态试验的激励点位置。
2 箱体试验模态分析
2.1 试验模态理论与方法
试验模态分析是研究复杂机械和工程结构振动的重要方法。它通过对激励力和响应的时域或频率分析,求得系统的频响函数,然后根据频响函数的特征,采用参数识别法求出结构的振动模态和结构参数,基本原理[8]如下:
变速箱箱体的振动可假设为一个具有n个自由度的线性时不变系统运动,其振动微分方程为:
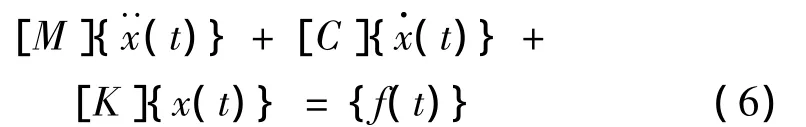
等式两边进行傅里叶变换得:
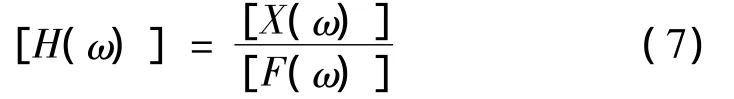
式中[H(ω)]为位移频响函数矩阵;
假设[φ]=[{φ1},{φ2},{φ3},…,{φn}]为结构的主振型矩阵,对于比例阻尼系统,在f点激励,第e点测量响应,位移频响函数为:
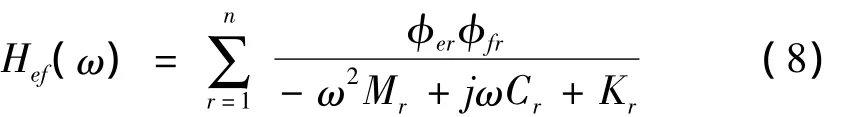
由于位移频响函数与加速度频响函数之间的关系为:
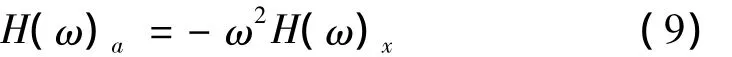
将式(8)代入式(9)中,得在f点激励,第e点测量响应,加速度频响函数为:
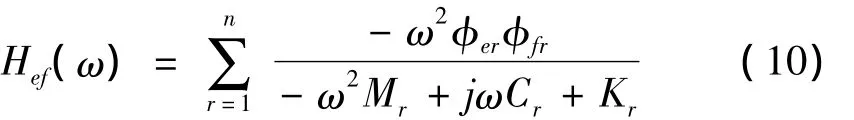
利用锤击法(SIMO)对结构进行试验模态分析,通常用加速度频响函数进行模态参数估计,为求振动模态,只要测定频率响应函数矩阵中的一行或一列即可。
2.2 箱体模态试验
本试验测试设备选用丹麦B&K公司8206型激振锤、4326型三轴向加速度传感器和比利时LMS公司的SC310DC-UTP型数据采集设备、LMS Test.Lab 9A版数据分析软件。根据预试验分析所确立的测点布置方案,建立箱体的模态试验模型,箱体外表面测点共152个,分别选取139-Y、101-X和19-Z方向作为激励点。
试验中对输入的激励力信号加力-指数窗,适时观察响应和激励之间的相干函数,剔除相干函数不理想、锤击质量不佳的测试数据,以提高激励信号的信噪比。每次试验锤击5次,并对测量数据进行线性平均处理,减少测量误差。由于试验对象是小阻尼系统,采样时间短、响应衰减慢,响应信号容易产生能量泄漏,需要对测点加速度响应信号加汉宁窗,提高了频响函数的精度。本试验将0~2000Hz作为试验测试频段。
对箱体进行单点激励多点响应的锤击模态试验,测量并记录各激励点作用下各测点的频响函数数据。利用Lms Test.Lab 9A软件的PolyMAX参数识别方法进行模态参数识别。识别出箱体在选定频段内的所有各阶模态参数,包括模态频率、阻尼比、模态质量、刚度和阻尼。由于振型矢量是相对值,采用不同尺度的振型矢量归一化,可得到不同的广义模态参数。最常用的方法是按模态质量归一化,箱体的前10阶模态参数如表2。
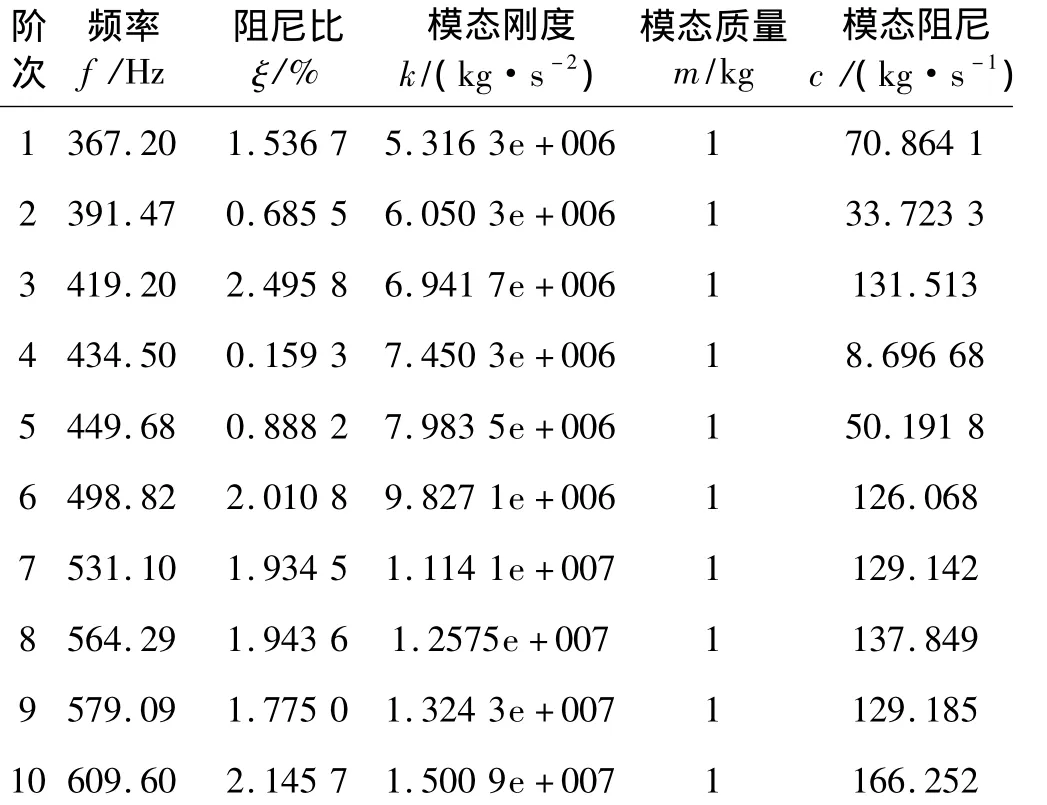
表2 箱体前10阶模态参数(模态质量归一化)Tab.2 Gearbox modal parameters of first 10 orders(unity modal mass)
对三个不同方向和位置的激励点进行锤击模态试验,得到各自频响函数总和曲线并进行比较,如图7所示,由图可知,综合比较曲线上的峰值个数和激振能量总体分布,139-Y方向激励效果最好,这与箱体预试验分析结果一致。
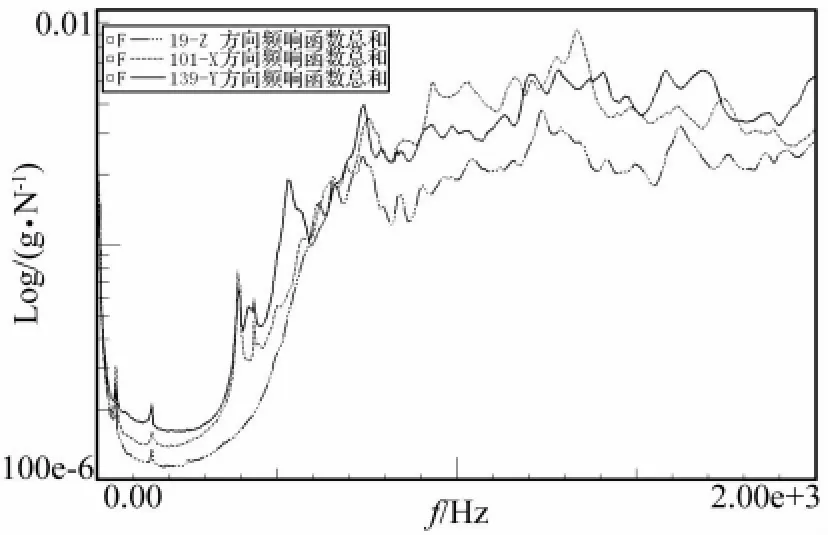
图7 不同激励点下频响函数总和Fig.7 SUM of FRF of Different Exciting Points
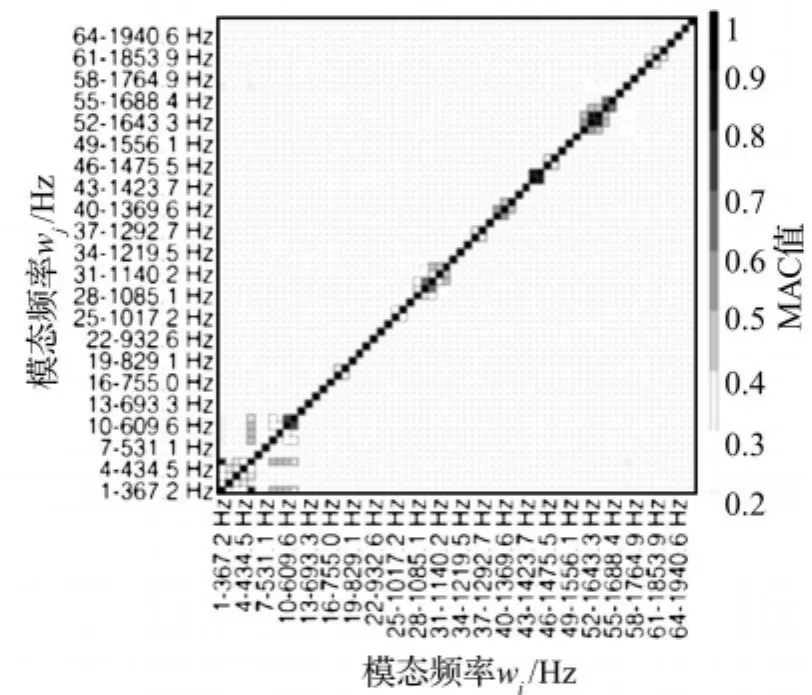
图8 试验模态置信准则图Fig.8 Experimental Modal Assurance Criterion
2.3 试验模态置信判据准则
对模态试验所得箱体各阶模态振型的相关性进行分析,利用MAC矩阵表绘制模态置信准则图,如图8所示。
由图8可知在MAC矩阵对角线上,值接近于1(100%),对角线外MAC远小于1。在低频范围内,模态振型存在空间混淆现象,这与箱体预试验分析时情况相同,因为实际模态测试时只能在箱体外表面布置传感器,低频各阶模态振型主要体现在箱体内部筋板的变化上。结合预试验分析结果,即使低频存在振型空间混淆,试验结果也是正确可信的,模态试验所识别的模态参数是箱体结构真实的模态参数。
3 结论
本文详细论述了模态预试验分析和模态试验分析理论,并以某型变速箱箱体为例,进行了锤击模态试验,并对试验结果进行比较分析。研究结果显示:
(1)在对复杂变速箱箱体这类结构进行模态试验之前,对其有限元模型进行预试验分析,可以很大程度地优化响应测点和激励点数目及位置。
(2)利用简单易行的锤击脉冲激振法可以对变速箱箱体这类复杂结构进行模态试验,并能充分激起结构的各阶模态,成功实现结构模态参数的识别。
(3)在不同的激励点位置和方向对箱体进行锤击模态试验,试验结果表明预试验分析确定的激励位置及方向是正确的。
(4)通过箱体模态试验与预试验分析所得的模态振型间相关性的比较,表明模态试验结果是可信的,可利用其进行有限元模型修正,以及计算结构的动力响应,进行结构的优化设计。
[1]夏江宁,陈志峰,等.基于动力学环境试验数据的模态参数识别[J].振动与冲击,2006,25(1):99-103.
[2]纪晓东,钱稼茹,等.模拟环境激励下结构模态参数识别试验研究[J].清华大学学报(自然科学版),2006,46(6):769-772.
[3]骆志高,李 举,等.基于试验模态分析的圆锯片降低振动研究[J].振动与冲击,2009,28(2):124-127.
[4]董小瑞,杨世文.复杂结构模态测试方法研究[J].兵工学报,2008,29(4):474 -477.
[5]Lallement G.Optimal selection of the measured degree of freedom and application to a method of parameter correction[C].Proceedings of the 9th International Modal Analysis Conference(IMAC).New York:Union College,1991:972-976.
[6]曹树谦,张文德,等.振动结构模态分析:理论、实验与应用[M].天津:天津大学出版社,2001.3.
[7]LMS Virtual.lab Noise&Vibration Pre - test Theore-tical Background[M].2004.
[8]沃德.海伦,斯蒂芬.拉门兹,等.模态分析理论与试验[M].北京:北京理工大学出版社,2001.

