斜拉桥主梁应变监测数据分析
周 毅,孙利民,闵志华
(同济大学 土木工程防灾国家重点实验室,上海 200092)
近年来,基于振动响应信息的结构健康监测已经得到越来越广泛的应用,许多国家和地区在一些已建的大跨度桥梁上安装了结构健康监测系统,如香港的青马大桥、韩国的Seohae桥和中国大陆的东海大桥等[1]。大多数结构健康监测系统不仅测量结构的响应,如位移、加速度、应力等,也监测结构所处的环境或者运营状况,如温度、风速/风向、相对湿度、交通荷载等。通常,健康监测的过程包括:通过一系列传感器的定时取样得到系统动力响应测量值,从这些测量值中抽取对损伤敏感的特征因子,并对这些特征因子进行统计分析,从而获得结构当前的健康状况信息,最终为结构维护、维修与管理决策提供依据和指导。
东海大桥健康监测系统自2006年9月成功运营以来,积累了大量的实测数据。在以往的健康监测数据分析中,人们利用较多的是加速度响应,因为加速度响应是一种稳态信号,可以很方便地得到结构的振型。对所获得的应变数据的利用主要是把握结构的绝对应力水平、混凝土结构的开裂和钢结构的疲劳等,而对无损伤或轻微损伤状态下的结构应变数据的利用研究还不多。Wang[2]等人基于经验模态分解(Empirical Mode Decomposition,简称EMD)分析方法对应变数据进行了处理,对一个由车辆过桥时产生的应变信号进行分离,从中提取了车辆的静荷载效应引起的应变信号,通过数值算例和试验分析验证了该方法的可行性。但其未对动态响应作进一步的分析。
根据车桥共振理论[3],本文用经验模态分解法(EMD)对东海大桥主航道斜拉桥的主梁应变监测数据进行了动、静分离,并基于分离出的动态应变响应识别了结构的频率信息;同时基于分离出的静态响应数据估计了车流量,初步探讨了结构应变监测数据的处理方法及利用价值。
1 主航道斜拉桥健康监测
东海大桥是我国第一座真正意义上的跨海大桥,起始于上海市南汇区芦潮港,北与沪芦高速公路相连,南跨杭州湾北部海域,直达浙江省嵊泗县小洋山岛,全长约32.5 km。大桥设主通航孔桥一座,为双塔单索面半漂浮体系叠合梁斜拉桥,主塔为倒Y型钢筋混凝土结构,塔高150 m,主跨420 m,为全线最大跨径桥梁。
为了保证东海大桥结构的安全性、耐久性和使用性能,提高大桥的维护管理水平,东海大桥上设计安装了结构健康监测系统。该系统共监测桥的8个区段,其中主航道斜拉桥位于第5区段,安装有169个传感器,实时监测该斜拉桥的加速度、位移、风速/风向、大气温度、结构温度、索力、结构应变、伸缩缝位移等(图1)。
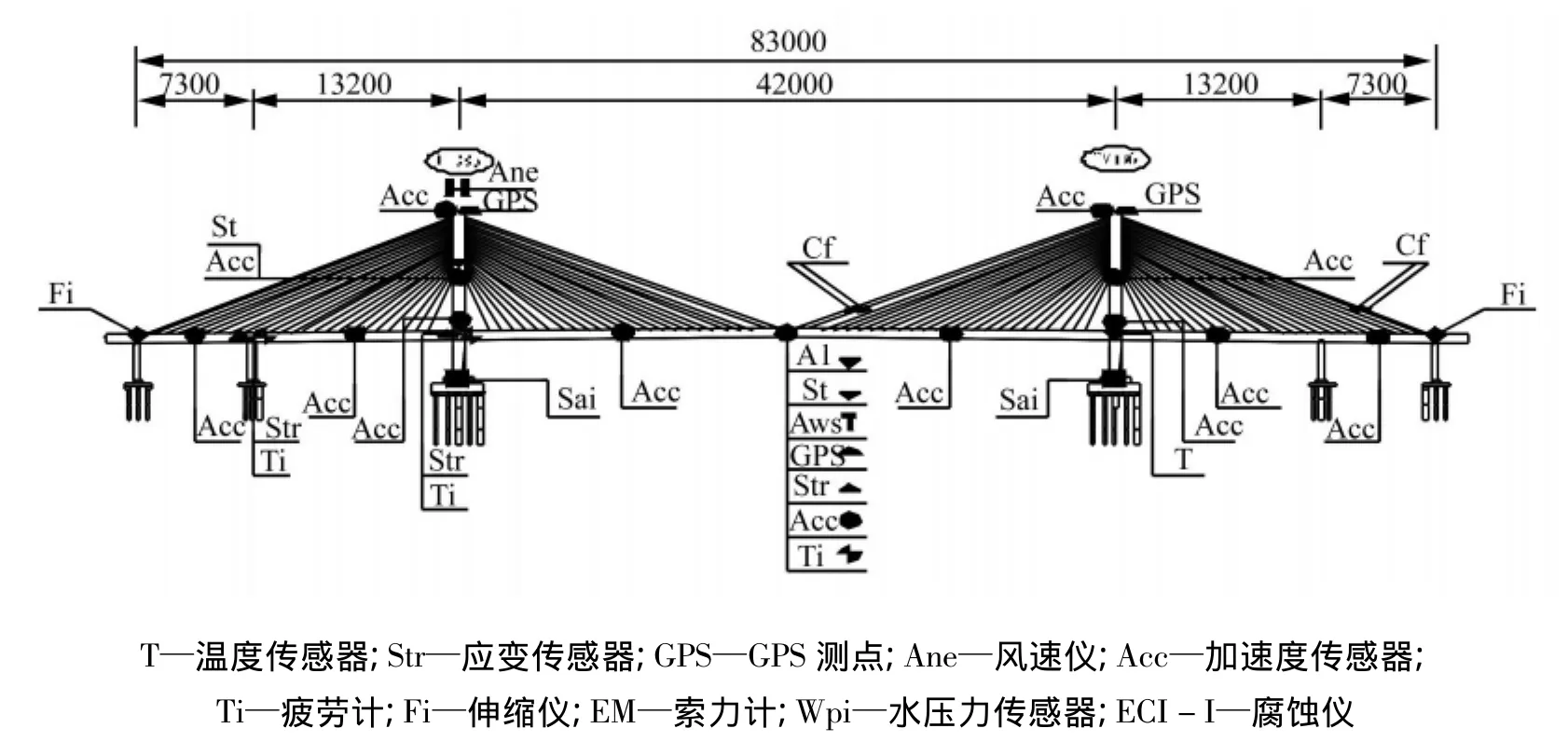
图1 主航道斜拉桥传感器布设示意图(单位:cm)Fig.1 Layout of the Sensors on the Main Navigation Channel Bridge
2 应变成分分离方法
2.1 移动车辆引起的桥梁振动
结构在移动荷载作用下的应变响应同位移响应类似,可视为长周期响应趋势与短周期扰动的叠加,这里分别称为静态响应成分和动态响应成分。求解结构在移动车辆作用下的响应,理论上大致可分为古典法和现代法两大类,本文采用俄国学者Крылов建立的古典分析方法。这里,车辆荷载用一个常量力F代替,不计车辆质量,即不考虑车桥耦合振动;桥梁模型采用质量均匀分布的等截面简支梁,跨径为l,其单位长度上的质量m以及抗弯刚度EI均假定为常数。当车辆F以匀速v通过简支梁时,梁挠度的动力响应表达式为:
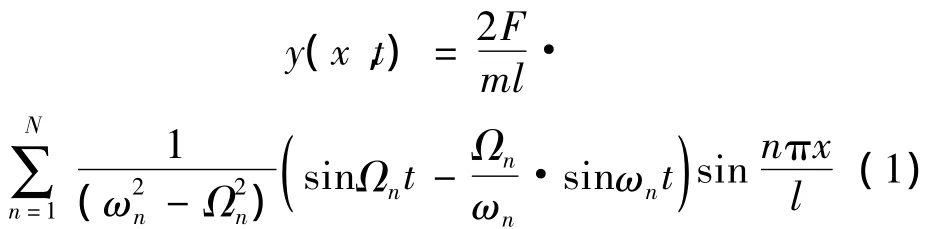
式(1)括号中的第一项就是静态响应,它的角频率Ωn=nπv/l与车速成正比,可以证明,其级数和与挠度影响线相似。第二项则是动态响应,它的角频率ωn=是结构的固有角频率。以一座简支梁桥为例,假定各项参数为:l=25 m,m=5148kg/m,F=550000N,v=10 m/s,EI=1.304 ×1010N·m2,则 Ω1=0.4 π,ω1=8 π;Ω2=0.8 π,ω2=32 π;Ω3=1.2 π,ω3=72 π……如果取式(1)中级数的前10项,该简支梁跨中的挠度时程将如图2所示。
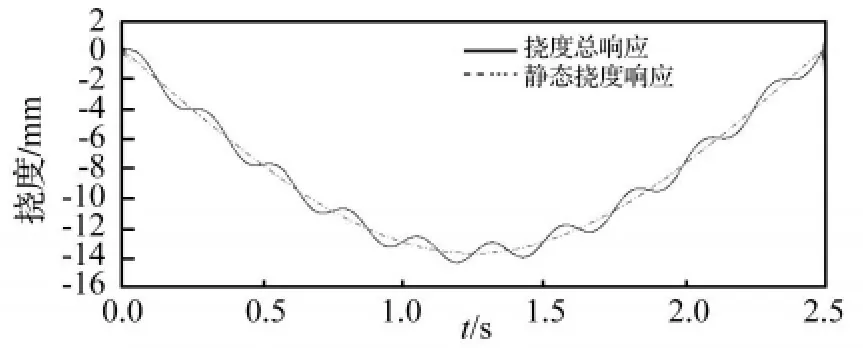
图2 匀速移动常量力引起的跨中挠度Fig.2 Mid-Span Deflexion under a Uniformly Moving Force
图2中的虚线就是式(1)中第一项sinΩnt累加的结果,反映了挠度响应的趋势,而图中的波浪线则是响应趋势与扰动叠加的结果。在目前的车速下,式(1)中的Ωn远小于ωn。正是动静响应成分在频率上的差异,使得它们的分离成为可能。
2.2 经验模态分解法(EMD)
移动车辆引起的桥梁振动是一种包含多种频率成分的非平稳信号。分离这类信号有多种方法,比如经验模态分解法(Empirical Mode Decomposition,简称EMD),多分辨率小波分析法(Multiresolution Analysis,简称MRA),主成分分析法(Principal Component Analysis,简称PCA)和独立成分分析法(Independent Component Analysis,简称ICA)等。PCA及ICA方法需要多测点的数据,而实际监测的数据通常点数较少,故较难取得好的效果,只适合于数值模拟信号的分析;相对来说EMD和MRA方法比较适合东海大桥实测应变数据的处理。本文选用EMD方法对东海大桥应变监测数据进行动静成分分离。
经验模态分解[4]是近年来由美籍华人科学家Huang提出的一种新的信号处理方法,它认为任何信号都由一些不同的固有振动模式构成,并据此将信号分解为若干个本征模函数(Intrinsic Mode Function,简称IMF)ci(t)及一个余项rn(t)的线性和。即:
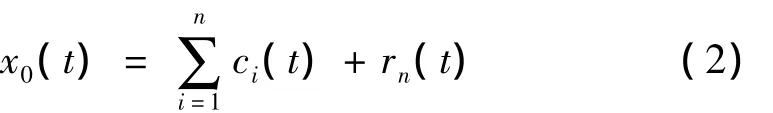
本征模函数 ci(t),i=1,2,…,n反映了信号中不同频率的成分。从原始信号中先分离出来的本征模函数的频率高,后分离出来的频率低,余项的频率最低。我们以结构基频为阈值,认为频率高于基频的本征模函数属于动态成分,它们的和等于结构动态响应;认为频率低于结构基频的本征模函数属于静态成分,把它们相加后得到结构静态响应。
3 数值试验验证
下面通过一个算例验证经验模态分解法在分离结构动静应变响应上的可行性。
该算例按与东海大桥主航道斜拉桥相近的跨径比采用5跨等截面连续梁模型,跨径布置为10+20+60+20+10 m(图3)。采用平面梁单元建立有限元模型,单元长度为 0.1 m,弹性模量 E=3.00 ×1010Pa,泊松比 μ =0.2,密度 ρ=2600kg/m3,截面积 A=9 m2,惯性矩I=11.75 m4,截面高h=3 m。移动车辆荷载按100 kN计,以20 m/s的速度过桥,时间步长为0.001 s。
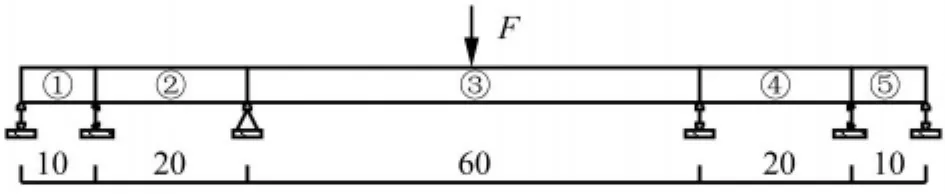
图3 连续梁模型(单位:m)Fig.3 FE - Model of the Continuous Beam(unit:m)
为了说明基于应变响应统计车辆数目的原理,这里假设有两辆车先后同方向通过该连续梁。第一辆车在t=0 s时上桥,在t=6.005 s时离桥;第二辆车t=9 s时上桥,t=15.005 s时离桥,程序计算至t=18 s。通过改变集中力作用位置模拟过桥车辆,求得主跨中点截面下缘的应变响应如图4所示。
利用经验模态分解法对该应变时程进行分解,得到6个本征模函数IMF和一个余项共7个分量。通过求每一个分量的自功率谱,可判断该分量的主要频率成分(图5)。从图中可以发现本征模函数的频率逐渐降低,第1阶的峰值频率接近3Hz,与结构基频f1=2.9891Hz相当,可以认为是高频成分,属于动态响应;而后面几阶IMF包括余项的峰值频率都远低于结构基频,属于低频成分,把它们相加后应该表示静态响应。
分离得到的动静应变响应如图6和图7。
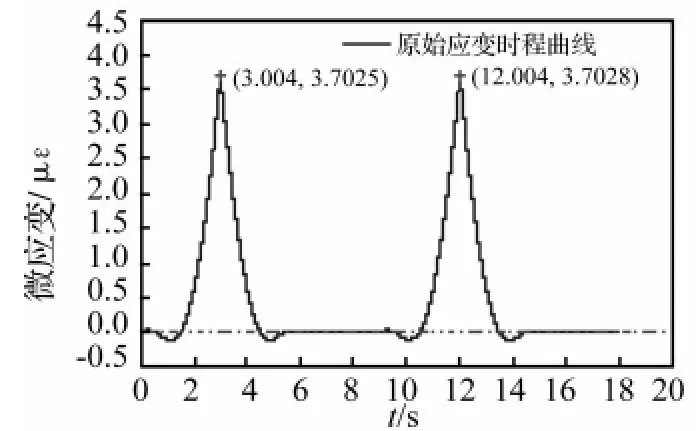
图4 连续梁模型主跨跨中原始总应变时程Fig.4 Total Strain History in Mid-Sapn of FEM
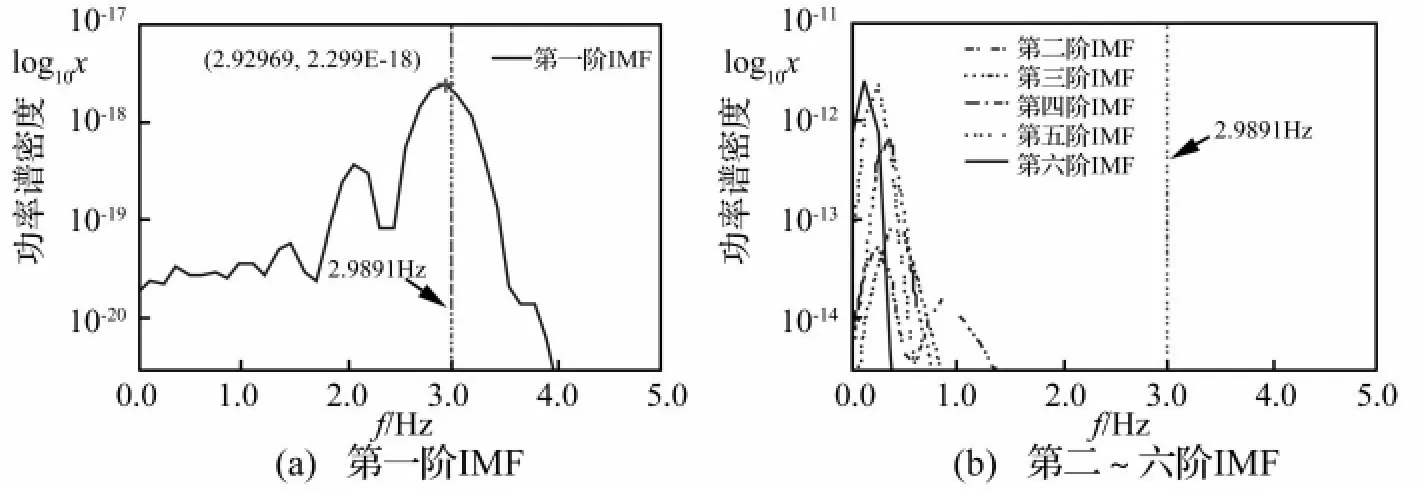
图5 应变的本征模函数IMF的频谱特性曲线Fig.5 Power Spectral Density of IMF
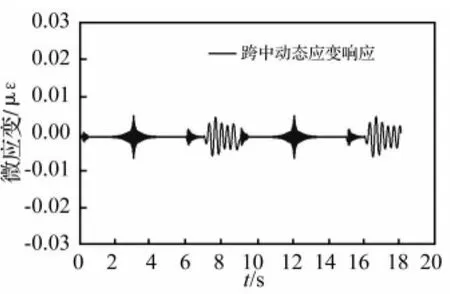
图6 动态应变响应成分时程曲线Fig.6 Time History of Dynamic Strain Response
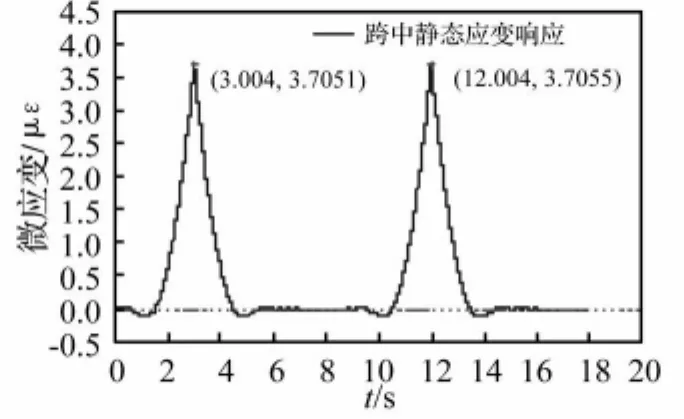
图7 静态应变响应成分时程曲线Fig.7 Time History of Static Strain Response
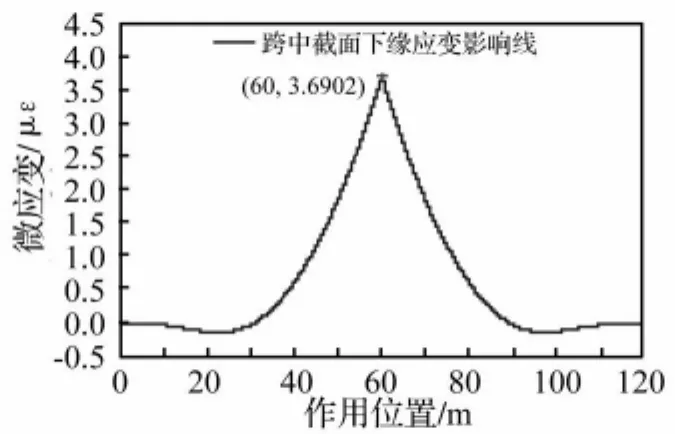
图8 连续梁跨中截面下缘应变影响线Fig.8 Influence Line of Strain at Bottom of Mid-Section
下面求动态应变响应的功率谱密度函数,并在结构一阶频率f1=2.9891Hz附近寻找功率谱密度极大值对应的频率。算例中动态应变响应只包含第一阶IMF,故其功率谱密度函数图形即为图5(a)。由图中可见,能量峰值位于fd=2.9297Hz附近,该频率即为由动态应变响应识别出来的结构基频。fd与结构基频f1=2.9891Hz之间的绝对误差为0.0594Hz,略小于频率分辨率0.061Hz,相对误差为2%。这说明基于经验模态分解法(EMD)所得结果识别结构基频的方法是可行的。
再将静态响应的时程曲线(图7)与模型结构的影响线(图8)作一比较。这里必须指出,结构某一量值的影响线是在单位移动荷载作用下表示该量值变化规律的图形,即相当于车辆缓行时的响应趋势,与时间t无关。所谓静态响应与影响线的比较,实际上是以车重和速度为系数对静态响应时程曲线进行缩放后的比较。方便起见,采用同样的重车进行影响线求解。
连续梁模型跨中截面下缘应变的影响线仍然用移动加载的方式获得,只不过此时要加大瞬态分析子步的时间步长,模拟荷载在不同位置的静力加载(图8)。
对比图7和图8可知,它们的最大应变十分接近,由EMD方法分离出的最大静态响应为3.7051μq、3.7055μq,与模型结构影响线的最大值3.6902μq 只相差了。这说明EMD方法的确分离出了跨中截面应变响应的趋势,用该方法进行响应动静分离是可行的。
图7的静态应变响应中最大的两个峰值是由两辆车匀速过桥产生的。利用5跨连续梁影响线的性质不难知道,一辆车过桥时在跨中应变响应时程曲线上将产生三个波峰和两个波谷(图8)。其中小车位于第1、3、5跨上时对应波峰,位于第2、4跨上时对应波谷。对于等跨径连续梁而言,跨中截面应变的影响线将呈现由中间向两边幅值逐渐递减的趋势。如果中跨跨径远大于边跨,则跨中截面应变的影响线将几乎只有一个明显的高峰,该峰值对应于小车恰好位于跨中的情况,就像数值算例中的一样。这种情况对于车辆数目的统计是最方便的。
车辆数目的识别精度与车速、车重、车距等因素有关。本文限于讨论单向车流的情况。利用数值模型计算两车过桥时的跨中应变后,可发现车速的影响不如车重、车距大。限于篇幅,图9展示了部分计算结果。
4 实测应变数据处理
4.1 实测应变数据动静成分分离
东海大桥主航道斜拉桥主梁采用钢-混凝土叠合梁,跨中断面上既布设有混凝土应变传感器,又有钢结构应变传感器。应变传感器均为光纤光栅传感器,布置如图10。
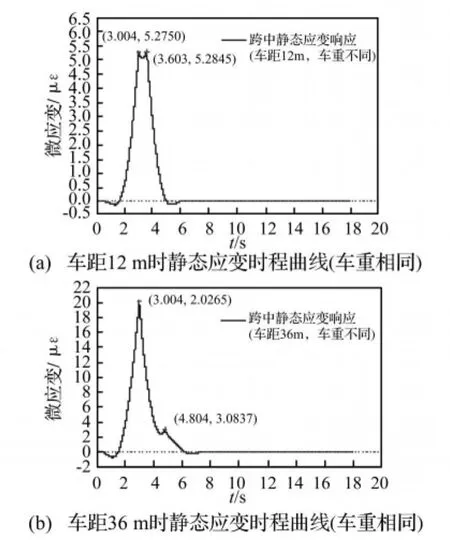
图9 不同情况下的静态应变响应时程Fig.9 Static Strain Responses in Different Cases
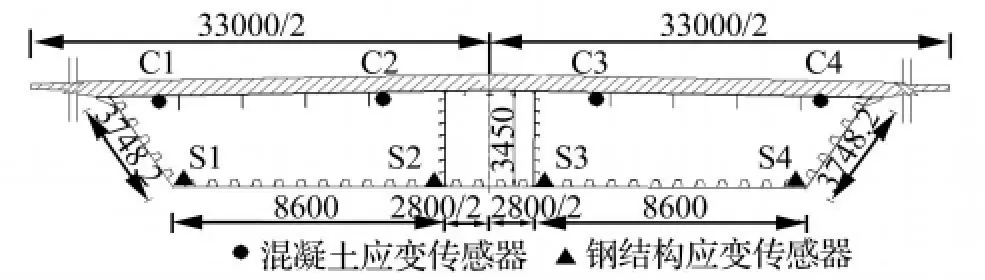
图10 主航道桥跨中断面应变传感器布置图(单位:mm)Fig.10 Layout of Strain Gauge on Mid-Section(unit:mm)
本文取东海大桥主航道斜拉桥跨中钢结构应变传感器S2和S3在2008年3月19日上午9点到10点一个小时内所测数据进行分析。同时为了能够在分离的结果中区分出动态应变响应和静态应变响应,选取该时间段内加速度响应计算出结构的基频为0.3662Hz,以此作为比较的标准。东海大桥主要通行车辆为集装箱卡车,且目前由于洋山港二期工程尚在建设中,交通量还不大,车辆荷载模式比较简单。
实际传感器存在“零偏”现象,即由于混凝土伸缩徐变,及传感器安装与工作时环境温度的不同导致测量得到的应变信号在无外界荷载激励时其中心不在零点。考虑到零点的偏移值主要与环境温度有关,而在一个小时内温度不会发生太大的变化,因此可假定一个小时内的所有数据点与零参考线偏移了同一个值C,即时程曲线整体平移了C。从应变时程曲线上可以找到一些相对平稳的数据段,它们应该表示桥上无车通过或者仅在边跨上有车辆行驶的情况。可用若干个这样平稳数据段的平均值表示C。在对实测数据中的零点偏移进行修正之后,本文先基于EMD方法对S2所测数据进行分解,得到了17个本征模函数和1个余项,共18个分量。对每一个分量进行自功率谱分析,可以发现第8阶以后的分量的主要频率明显小于结构基频0.3662Hz(图11)。把第8阶以后的分量相加得到静态应变响应,而1阶~7阶分量相加得到动态应变响应。
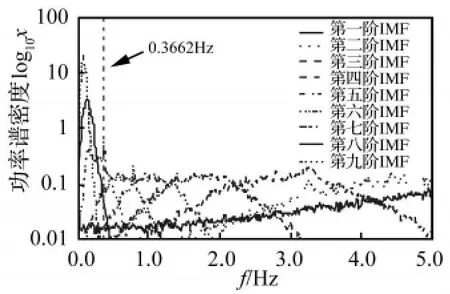
图11 前9阶IMF频谱特性曲线(S2传感器)Fig.11 PSD of the 1st to 9th IMFs(S2 Sensor)
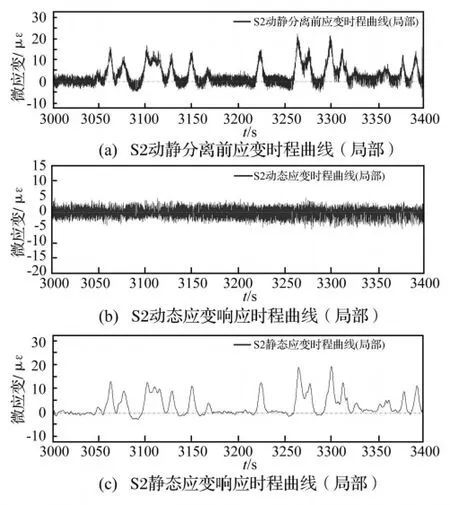
图12 S2传感器所测应变响应分离结果(局部)Fig.12 the Decomposition of Strain Measured by S2(Part)
图12是S2传感器实测应变动静分离前后的情况,从图中可以发现,原始信号中的趋势成分与扰动成分被较好地分离开来。
对S3传感器的数据可以同样处理,结果与S2基本相同,限于篇幅,结果不再详述。
4.2 基于动态响应数据的应用
首先求出S2的动态应变响应的自功率谱(图13)。在0.3Hz~0.5Hz的范围内功率谱密度最大值所对应的频率为0.3693Hz,该值即为通过动态应变响应求得的结构基频。它非常接近于由加速度响应识别的一阶频率0.3662Hz,两者相对误差只有0.8%。从图中也可以看到二阶对称竖弯模态频率0.7813Hz,它与由加速度响应得到的值0.7874Hz也只有0.8%的相对误差。为了对比,把原始信号的自功率谱绘于图14中,前几阶频率不如图13明显。
同理,可以得到S3传感器动态响应的频谱特性曲线,从中获得的结构一阶频率恰为0.3662Hz,而二阶对称竖弯模态频率仍为0.7813Hz。
由上述两个传感器的处理结果不难发现,实测应变数据经EMD分离得到的动态响应可以识别出结构的低阶频率,这主要是因为应变响应对于结构的低阶频率更加敏感。尽管加速度信号功率谱密度曲线的峰值更为明显,但是使用应变传感器通常更为经济。因此,东海大桥主航道斜拉桥基频的成功求解,对于健康监测系统应变数据处理方法的研究和充分利用还是很有意义的。
4.3 基于静态响应数据的应用
东海大桥主航道斜拉桥上的车辆主要为往返于上海和洋山港之间的集装箱卡车,交通流特性较单纯,有以下两个特点:
(1)车辆过桥速度均匀。在利用静态应变响应对车辆进行计数时,本文假设车速均匀,在数值算例中也未对变速过桥的情况作讨论。这是因为东海大桥非常长,而主航道斜拉桥只是中间的一小段,车辆在上面行驶时几乎不存在变速的问题,故可认为行车速度均匀。
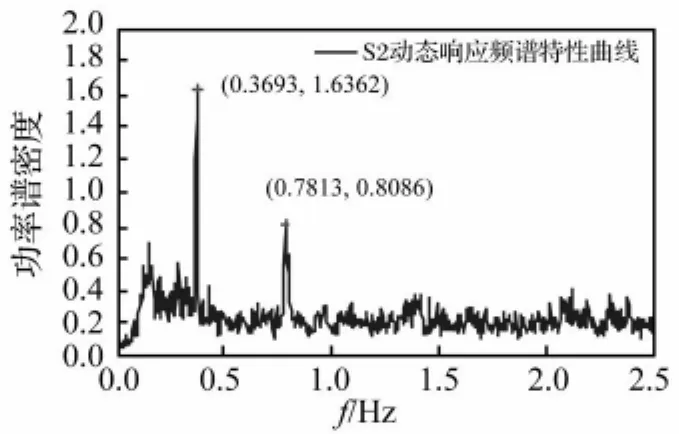
图13 动态应变响应频谱特性曲线(S2传感器)Fig.13 PSD of Dynamic Strain Response(S2 Sensor)
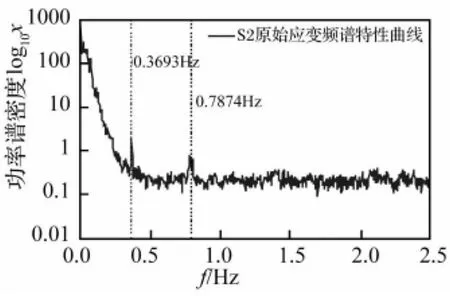
图14 总应变响应频谱特性曲线(S2传感器)Fig.14 PSD of Total Strain Response(S2 Sensor)
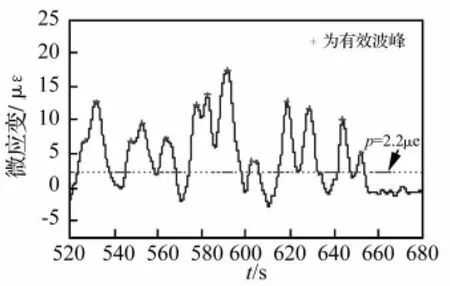
图15 S2静态应变时程曲线中识别出的有效波峰(局部)Fig.15 Effective Peaks on Static Strain Curve of S2(Part)
(2)过桥车辆以大、中型车辆为主。这是因为东海大桥主要为洋山深水港区运输货物的集装箱卡车服务,这些大、中型车辆过桥时产生的应变响应较明显,对大桥疲劳和受力特性的影响远大于小型车辆。所以对于评估大桥结构健康状况而言,即使由于识别精度问题遗漏了部分小型车辆,对桥梁评估的影响也不大。
东海大桥主航道斜拉桥与算例中的5跨连续梁相似,中跨跨径远大于边跨,车辆在边跨行驶远不及在中跨行驶时对跨中断面应变的影响大。本文采用统计跨中断面应变高峰数量的方法对过桥车辆进行计数。基本思路为:找出时程曲线上振幅大于h的波形的极大值点。为了不遗漏所有极值点,h的值可适当取小。由于经验模态分解法分离出的静态应变在零参考线附近会有波动,而且车辆在边跨上行驶时也会在应变波形中产生波峰,所以应再设置一个阈值p,把时程曲线上应变值小于p的峰值点删除,最后剩下的波峰数即为过桥车辆数。
如图15所示,首先找出S2传感器的静态应变响应时程曲线上振幅大于h的所有极值点,包括波峰和波谷。为了保证车距较近的两辆车能被准确识别,阈值h适当取小,最终取h=0.01 με。然后删除波谷对应的极值点,再设置一个阈值p,把应变值小于p的波峰删除,排除小幅波动的影响。最后统计得到的波峰数才是过桥车辆的数目。p值的确定方法与h值相似,可以通过观察静态应变响应时程曲线得到。对S2传感器,p可以取为2.2 με,有效波峰有218个。
同理,我们也可以通过S3传感器的静态应变响应估计过桥车辆数目。通过观察静态应变波形可以确定参数 h=0.01 με,参数 p=2.5 με,识别出的过桥车辆为238辆。
综合考虑两个传感器的识别结果,可以粗略地估计2008年3月19日上午9点到10点一小时内过桥车辆约有228辆。
总的说来,从健康监测系统测得的应变响应中精确识别过桥车辆数目还相当困难。上述统计静态应变响应曲线有效波峰数量的方法受到很多人为因素的干扰,尤其表现在参数h和p值的确定上。若要使参数的选择尽可能客观,则需要结合交通视频、荷载标定实验等手段,对车重、车速与跨中应变响应之间的关系做更为深入的研究。由于预算原因,东海大桥结构健康监测系统中未能安装动态轴重仪对车辆荷载进行监测。因此,以上静态应变数据的利用很好地补充了相应的信息。
5 结论
本文对东海大桥主航道斜拉桥实测应变数据进行了处理,并简单讨论了监测数据的利用价值,从中可得到如下结论:
(1)经验模态分解(EMD)法可以实现结构应变响应的动、静成分分离,两种成分的分离以结构基频为界。在实际应用中,作为分离阈值的基频的准确度不必很高,所以可以通过数值计算、经验公式等方法获得。
(2)基于EMD方法对实测数据进行动静分离后,其中的静态响应可粗略估计过桥车辆的数目,而动态响应可以估算结构的模态频率。
本文只是对应变监测数据的初步探讨,在理论和实践上仍然存在不少问题。比如:采用经验模态分解法进行应变信号分离时的端点效应如何处理?本征模函数IMF的物理意义如何?各IMF之间的频率混淆问题如何解决?如果有多辆车同时经过跨中断面或者是双向车流,如何从静态应变响应中估计车流量?这些问题的解决有待进一步的研究。
[1]Sun L M,Sun Z,Dan D H,et al.Large-span bridge and their health monitoring systems in China[C].//Fan L.C.,Sun L.M.,Sun Z..Preoceeding of 2007 International Symposium on Integrated Life-Cycle Design and Management of Infrastructure. Shanghai:TongjiUniversityPress, 2007:79-95.
[2]Wang X M,Huang F L,Ma G,et al.Application of Empirical Mode Decomposition to Process Measured Strain Responses of a Bridge[C].//Ren W.X.,Hong H.,Zhu X.Q.Structural Condition Assessment,Monitoring and Improvement.Beijing:Science Press,2007.11.Vol.2:940 -944.
[3]李国豪.桥梁结构稳定与振动[M].第2版.北京:中国铁道出版社,2002.
[4]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstation time series analysis[J].Proceedings of the Royal Society of London.1998,A454:903-995.
[5]张启伟.大型桥梁健康监测概念与监测系统设计[J].同济大学学报,2001,29(1):65 -69.
[6]谢 峻,江见鲸,王国亮,等.大跨度预应力混凝土箱梁桥的健康监测系统[J].清华大学学报(自然科学版),2006,46(12):1957-1960.

