基于改进D-S证据理论的水下航行器声隐身性能评估

汤智胤，何 琳

(海军工程大学 船舶与动力学院，振动与噪声研究所，武汉 430033)

水下航行器的隐身性是水下航行器最基本的技术性能，其中声隐身性能则是决定其隐身性的最重要因素。水下航行器的隐身安全性历来被认为是头等重要的问题［1］。传统上，在中、低频常采用有限元 +边界元［2］;在高频常采用统计能量法对壳体辐射声计算［3］，以此判断水下航行器的声隐身性能。有限元+边界元方法基本原理是用有限元方法描述弹性结构的振动问题，用边界元方法来描述结构的声辐射场，将有限元方法和边界元方法在弹性结构与流体交界面上的离散化点相匹配，从而获得结构与声场的耦合运动方程。统计能量法是把研究对象划分成子系统后，假定每个子系统的模态参数的统计分布为已知的统计母体，使用子系统的动力学能量来描述系统的状态，利用能量变量就可使用简单的功率流平衡方程来描述耦合子系统间的相互作用，使用能量变量统一处理结构、声场等子系统间的相互作用问题［4］。虽然上述做法精度较高，但是速度慢，达不到快速计算的要求。实际应用中，对水下航行器隐身性需求，实时性要比精度更重要更具实战效应。如何选择合适而准确的方法，快速评估水下航行器声隐身性是一项复杂而重要的问题。

现代先进的水下航行器上都安装有包括力传感器、速度传感器、加速度传感器等在内的大量传感器。我们认为，对于该问题的工程解决方案，可以将数值计算问题变为基于多传感器信息融合的模式识别问题来解决。即:不直接计算航行器辐射声的具体大小，而是事先将航行器的声隐身性分为有限的若干类;当航行器运行时，通过传感器组采集的数据，将其声隐身性归为其中某一类，作为其声隐身性评估结果。这样一来，就将复杂的数值计算问题进行了合理简化，满足了实时性的要求。

1 模型的提出

传统对水下航行器声隐身性的评估，都是通过直接计算其辐射噪声来实现。但水下航行器的复杂结构决定了其巨大的辐射噪声计算量，实时性得不到保证。然而现代战争中，评估的实时性是水下航行器安全性的基本保证。实战中若丧失了实时性，其声隐身性评估则毫无意义。

多传感器信息融合技术在近二三十年来取得了快速的发展。而其中D－S证据理论是处理不确定性问题时的一个有用的方法。它已广泛用于信息融合和不确定性推理等领域，能在不需要先验概率的情况下，以简单的推理形式，得出较好的融合结果。

现代水下航行器上安装数目最多的是壳体振动加速度传感器(也称加速度计)。本文避开水下航行器复杂的辐射声计算而采用多传感器信息融合的手段，直接利用布置在航行器壳体表面的多个加速度传感器的实测时域信号，进行变换算出功率谱信号作为特征，然后用一种改进的D－S证据理论方法进行数据融合，提高了评估效率，能够很好地解决水下航行器声隐身性评估的实效性问题，从而实现水下航行器声隐身性的快速评估。评估过程如图1所示。

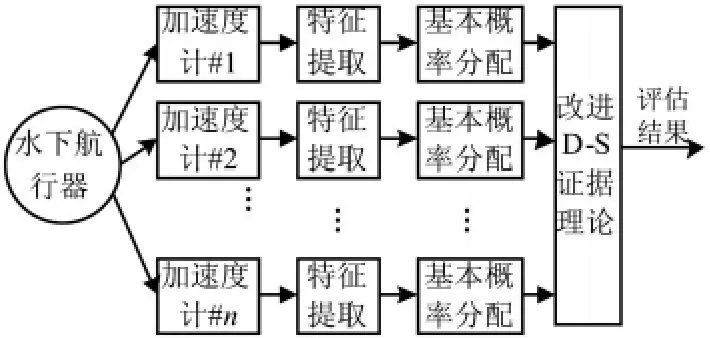
图1 基于改进D－S证据理论的水下航行器声隐身性能评估模型Fig.1 Acoustic stealth situation assessment model of underwater vehicle based on Improved D－S Theory

2 特征提取及基本概率分配

水下航行器辐射噪声时，认为系统在大多数情况下都是线性的。航行器声隐身性是其辐射噪声决定的，而辐射噪声又是航行器壳体振动所引起的。基于线形系统的假设，所以辐射噪声所研究的频段应与壳体振动研究的频段一致。

2.1 特征提取

设壳体上有n个可用的振动加速度传感器，水下航行器的辐射声能量绝大部分集中于从fdown到fup频率范围内，其它频段的能量很小。航行器声隐身性能全部由这个频段内的辐射噪声所决定。基于系统线性假设，壳体振动的能量分布也在从fdown到fup频率范围内。取航行器壳体n个加速度传感器的实测值，并分析从频率fdown到fup之间的范围。设从fdown到fup有r个点，计算出这些点的功率，并将其排列组成向量，作为水下航行器各传感器振动加速度的特征向量。

2.2 基本概率分配函数

本文基本概率分配函数的确定方法为:将进行水下声学实验时所测各性能级别的所有传感器数据作为基准，将实时测量的所有传感器数据分别对其进行比较，计算出实测数据与基准数据间的距离，并对其进行归一化处理，以此作为基本概率分配函数。具体步骤如下:

假设航行器声隐身性能有L个级别，加速度传感器共n个。将从fdown到fup的r个点，每个点的功率作为一维特征，即每个加速度传感器测得的样本可转化为一个r维的特征向量。

设性能级别为l(l=1，2，…，L)时，加速度传感器a(a∈{1，2，…，n})的基准特征向量为评估时刻，加速度传感器a实测值的特征向量为:ap=［ap1，ap2，…，apr。将二者之间的距离记为。对于单个传感器，计算出实测值的特征向量和所有性能基准向量的距离，并将归一化处理的结果作为各性能下的基本分配函数值，即:am(l)=这里的距离将用到一种图像欧式距离(Image Euclidean Distance)［5，6］:

设e1，e2，…，eR为对应R维空间的一组基向量，向量 p=［p1，p2，…，pR］T=p1e1+p2e2，…，pReR。图像欧式距离IMED(image euclidean distance)定义为:

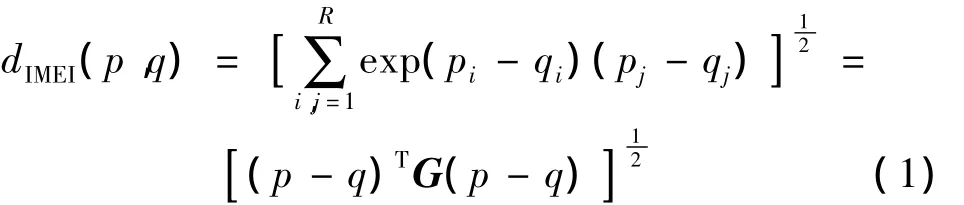
其中对称矩阵 G=(gij)R×R称为度量矩阵，gij(i，j=1，…，R)称为度量系数定义为:

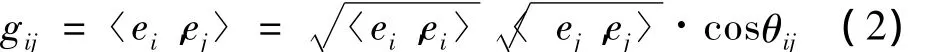
式中，〈，〉表示内积运算，θij是 ei和 ej间的夹角。常用的高斯函数所构造的图像欧式距离为:

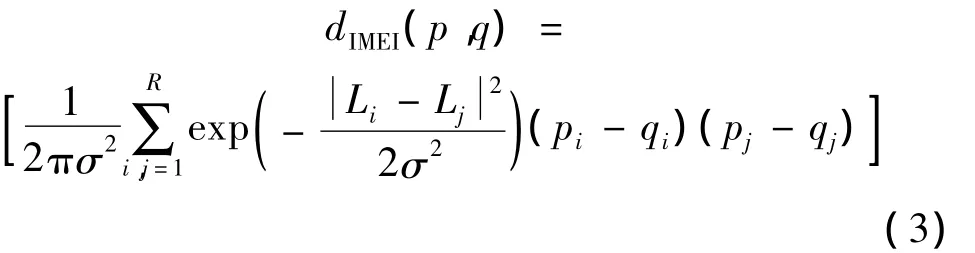
图像欧式距离和传统欧式距离的本质区别是:传统欧式距离没有考虑元素之间的空间关系，其基向量是完全独立的。而图像欧式距离则考虑了元素之间的空间关系，并体现在了度量系数中。

3 证据合成理论

由于其坚实的理论依据，D－S证据理论在很多情况下都能很好地进行信息融合，并得到与人们的直观认识相一致的结果。但当证据源出现矛盾，甚至冲突时，D －S 证据理论合成公式将会失效［7－9］。

本文采用一种基于证据特征的证据合成规则［10，11］，进行水下航行器声隐身性能评估。经计算仿真验证，它要比传统的Dempster证据合成规则和Yager证据合成规则的效果更好，结果也更符合实际解释。对于识别框架Θ，整个空间的大小为2N，其子集记为:A1，A2，…，A2N。两个证据m1和m2之间的距离为:

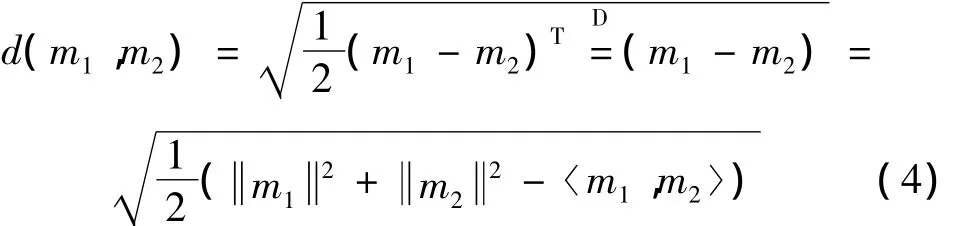
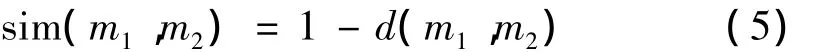
若有K个证据时，证据群体可靠性ε为:

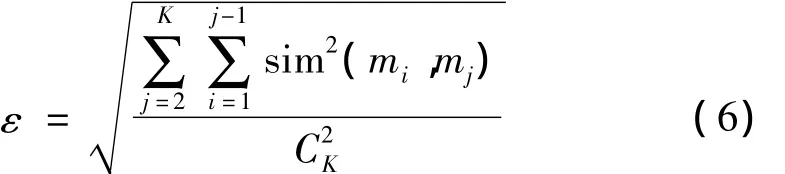
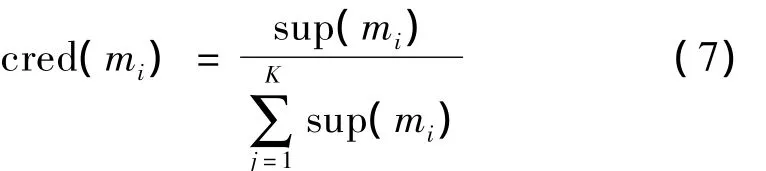
本文的证据合成规则，基于冲突信息可以利用，证据合成规则为:

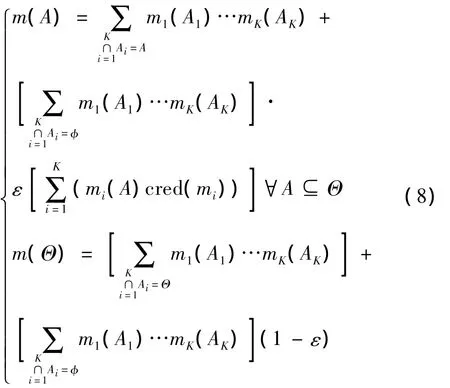
利用(8)式计算证据合成后的基本概率分配，分别求出所有状态的信任函数Bel，比较所有状态的信任函数值的大小，判定值最大的状态为当前的航行器声隐身性能级别。

4 应用实例分析

为测试方法的评估能力，我们进行以下仿真和实验。

4.1 几种距离的比较

比较两种信号的欧式距离、Hausdorff距离和图像欧氏距离的差异。

图2～图5中，红色图线表示的信号在4幅图中是一样的，蓝色图线代表的信号略有差异。

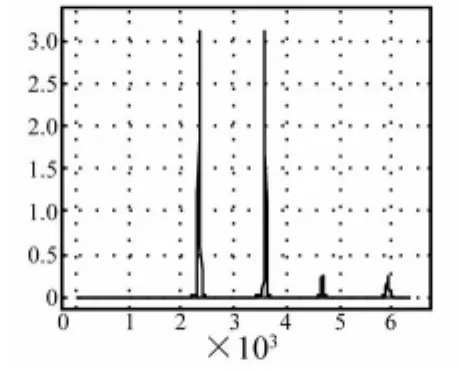
图2 两不同信号比较(1)Fig.2 Two different signals(1)

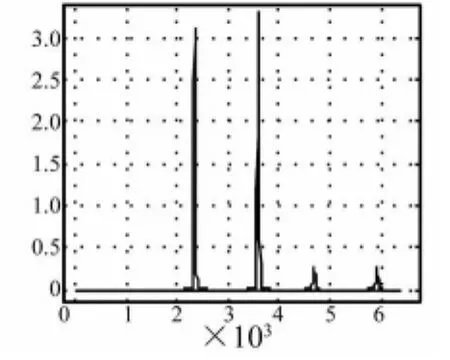
图3 两不同信号比较(2)Fig.3 Two different signals(2)

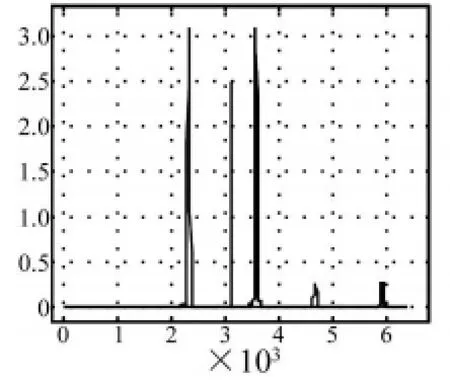
图4 两不同信号比较(3)Fig.4 Two different signals(3)

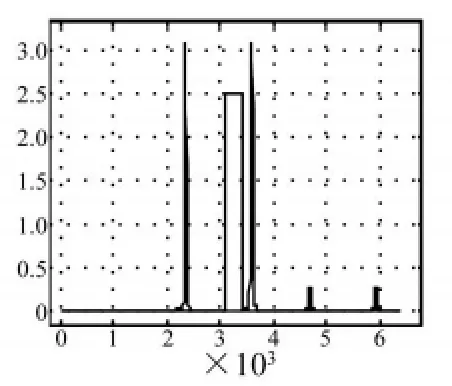
图5 两不同信号比较(4)Fig.5 Two different signals(4)

如图2所示红色和蓝色两个信号相比，仅有频率的漂移，欧式距离 dE=9.9039，Hausdorff距离 dH=1.1418 ×10－5，图像欧氏距离 dI=6.1631。当两个信号在形状上相似，而在位置上不同时，二者的Hausdorff距离比欧式距离和图像欧氏距离都要小，图像欧氏距离次之，欧式距离最大。

图3和图2相比，蓝色信号仅有最大值点比原信号的最大值大5%，其欧式距离dE=9.9540，Hausdorff距离 dH=0.15570，图像欧氏距离 dI=6.1929。其欧氏距离和图像欧氏距离都与图2中的相差不超过0.51%，而Hausdorff距离竟相差10982倍。

图4中蓝色信号比图2中的多了一个尖峰，欧式距离 dE=10.214，Hausdorff距离 dH=0.017693，图像欧氏距离dI=6.2433;图5中蓝色信号比图2中多出的一部分方波，其峰值与图4中的多出的尖峰峰值相等，欧式距离 dE=20.414，Hausdorff距离 dH=0.017693，图像欧氏距离 dI=12.779。

比较图4和图5，两图中蓝色信号的形状差别相当大，而它们与红色图线的 Hausdorff距离相等，说明Hausdorff距离进行信号形状比较时，主要是提取边缘，然后再进行相似性度量，它对信号局部的变形也不是很敏感。而另一方面，如果噪声对信号的极值造成影响，则有可能在计算Hausdorff距离时产生严重误差。

欧氏距离虽然能很好地度量两信号间的差异，对个别点的噪声也不很敏感，但对于仅存在位置差异，而形状相似的信号，却不能很好的描述。

而图像欧氏距离却能兼顾欧式距离和Hausdorff距离之间的优点，对形状相似的信号可以较好地度量，而对信号局部噪声的敏感度也较小。

表1 图2～图4中两信号的距离Tab.1 The distances between two signals in Fig.2 ～4

4.2 几种证据合成方法的比较

假设有识别框架 Θ={A1，A2，A3}，5个证据源，分别是证据源 m1为:m1(A1)=0.98，m1(A2)=0.01，m1(A3)=0.01;m2为:m2(A1)=0.98，m2(A2)=0.01，m2(A3)=0.01;m3为:m3(A1)=0，m3(A2)=0.99，m3(A3)=0.01;m4为:m4(A1)=0.98;m4(A2)=0.01，m4(A3)=0.01;m5为:m5(A1)=0.98;m5(A2)=0.01，m5(A3)=0.01。这5个证据源可以代表这样的情况:所有传感器对状态都是A1都是较大程度地支持，(有可能是故障或较强的局部噪声所导致的)仅有一个传感器m3对A1进行了全部否定，而较大程度地支持了A2。观察表2的证据合成结果，发现经典的证据合成方法在m2出现之前，三种方法的合成结果差别不大。而当m3出现之后，三种方法出现了显著的差别:由于m3对A1的全部否定，造成即使后面所有的证据都支持A1，用D－S证据合成方法，m(A1)始终为0，并将较大程度的支持分配给A2;而用Yager证据合成方法m(A1)也是始终为0，m(A2)和m(A3)也都随着证据源的个数增大而不断减小，并将绝大多数的支持全部分配给了全域。这两种合成结果显然是与实际常理相违背的。而用本文的证据合成方法，即使出现了一个与大多数正确证据源相冲突的错误证据源，合成结果也会随着正确证据源个数的增大而逐渐收敛到合理的结果，降低了错误证据源对信息融合结果的影响。

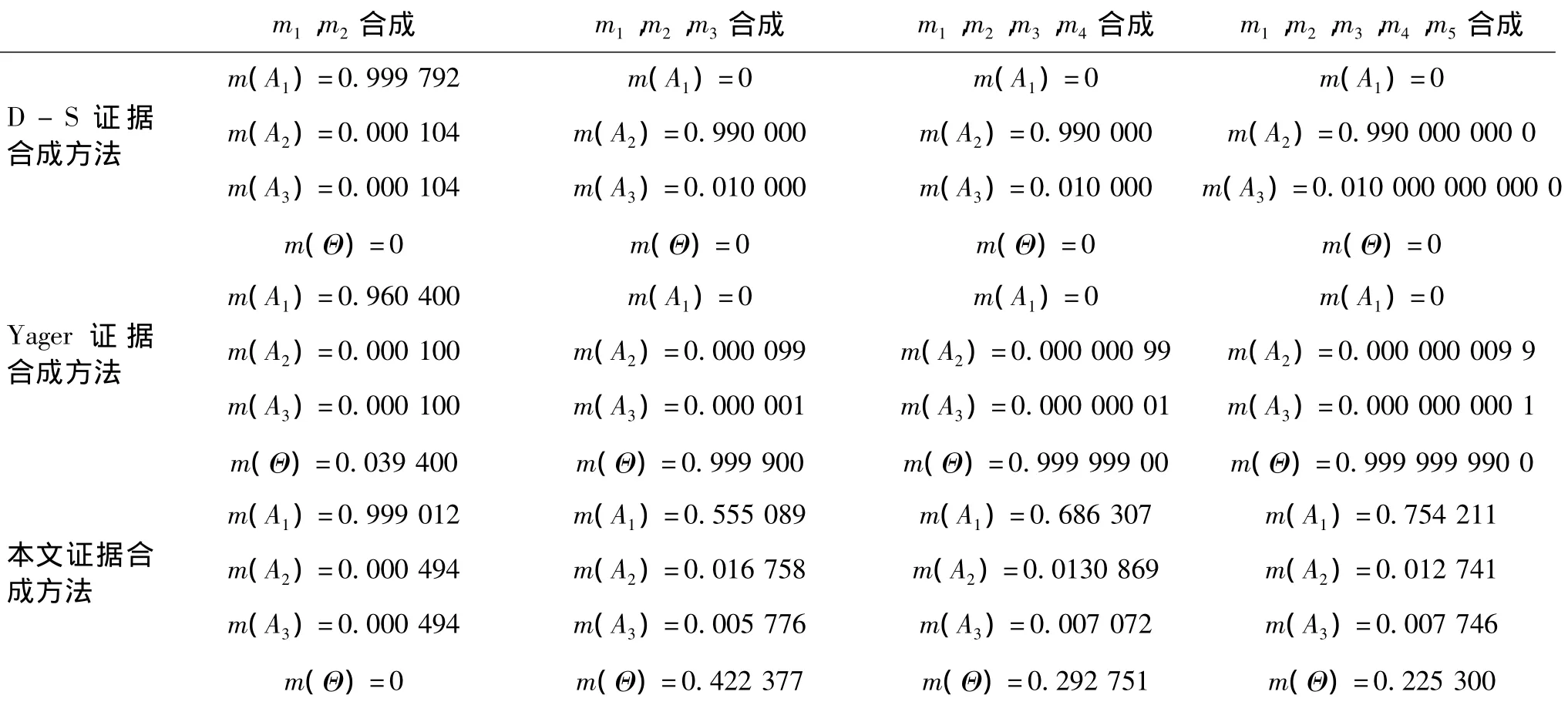
表2 不同证据合成公式对比Tab.2 Different results based on different evidence theories

4.3 不同个数证据源合成结果的比较

利用铁制双层加肋圆柱壳体进行水下声学实验。壳体外直径560mm，内直径400mm，高600mm。壳体内部安装3个激振器，模拟航行器内部机械装置对艇体的激励，在壳体表面上布置15个加速度传感器。根据模型的对称性，在内壳体内部布置3个激励点和10个加速度传感器，外壳体外表面布置17个加速度传感器。其布置方式如图6所示。表面加盖并密封，置于深约70 m，面积约250 m×1000 m的水库中;壳体布放位置离岸最近60 m，顶部离水面1.7 m;离壳体表面1m处，悬垂一个水听器，如图7所示。

实验设备为:

(1)信号发生器:用DP测量系统产生2路信号，用信号发生器产生1路信号;

(2)功率放大器2个:YE2706、YE5872;

(3)电磁激振器3台:JZK－2两台、JZK－20一台;

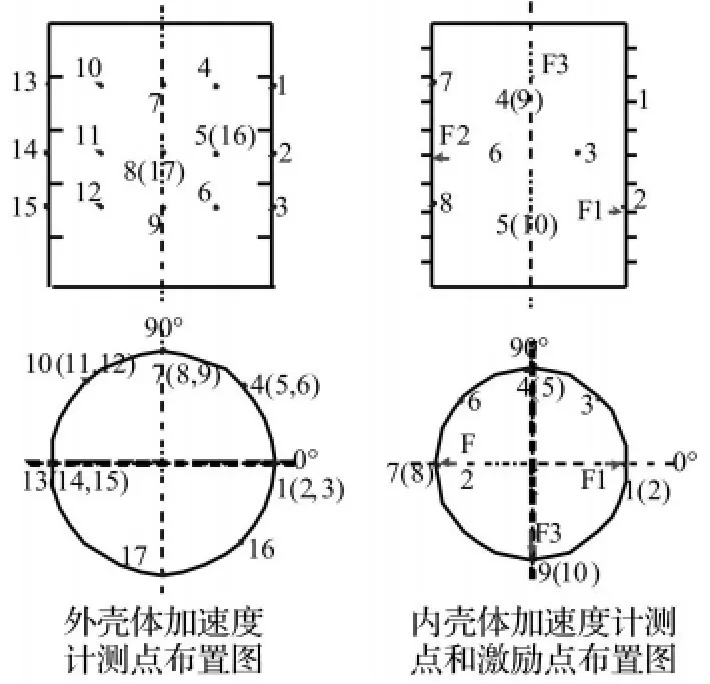
图6 内外壳体激励点、加速度测点布置图Fig.6 Position of vibration points ＆ Accelerometers

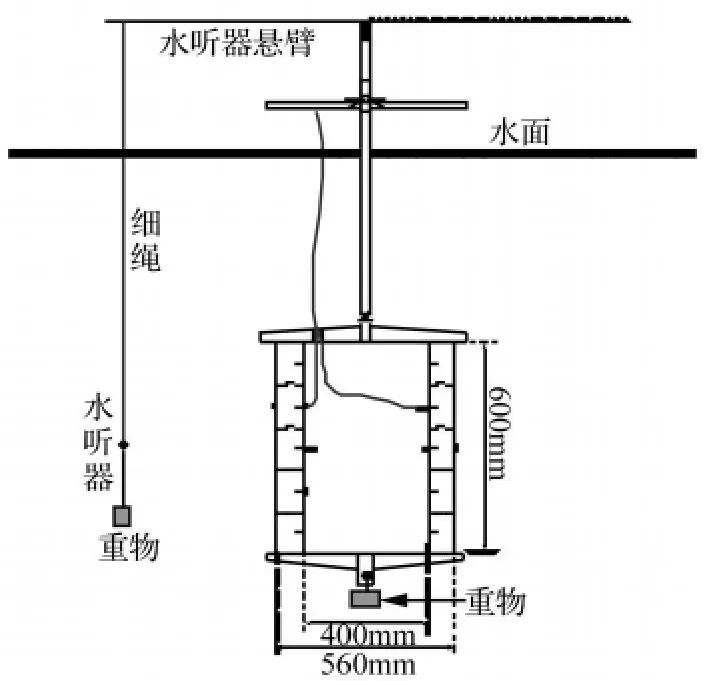
图7 双层圆柱壳体水下试验安装示意图Fig.7 Installation drawing of the equipment

(4)电荷放大器2个(信号放大、带通滤波);

(5)加速度传感器27个(内10外17):ICP加速度传感器(KD1002LC);

(6)32通道采集调理设备;

进行水下实验时，用壳体内部的电磁激振器激励壳体振动，测量内外壳体表面上的加速度信号。激励工况有单点激励，双点组合激励和三点同时激励;激励信号有白噪声和单频稳态正弦信号。实验采样频率为6400Hz，采样时间 4 s，声压基准值为 1 μPa。

评估时可将其声隐身状态分为:n类，n的取值可根据需要来定。不失一般性，本文中取n=3，分别对应#1、#2、#3激振器的激励情况。每个状态选择9个工况进行评估。评估时随机选取不同个数的传感器，用三种不同距离形成证据，并用本文中的改进D－S证据合成方法进行证据合成，比较评估正确率，结果如表3所示。

从表3中，我们可以发现虽然利用图像欧氏距离产生的证据能达到最大的正确率，但是与直观认识相矛盾的是证据源个数和评估正确率之间没有明显的规律。而且利用内壳传感器信息的识别正确率，不一定比用外壳传感器的正确率低。这是因为证据理论的基础是基于大多数证据都是支持正确命题的假设。然而实际中并不是完全符合这一假设，所以对证据源的选择，即传感器数据的选取方法还需要进一步地研究。

另一方面，用三种距离的识别方法其计算时间都会随着证据源个数的增大而增大。当选用10个内壳传感器和17个外壳传感器时，时间最长:用欧式距离最长计算时间7 s以内;用Hausdorff距离最长计算时间520 s;用图像欧氏距离最长计算时间316 s。如果要将此方法应用到实际中，传感器个数将是数以百计，计算时间也会成倍增长。但即使如此，也比传统辐射噪声计算方法的时间要短得多。

表3 不同个数传感器信息融合结果对比Tab.3 Different results based on different number of accelerometers

5 结论

本文针对以往水下航行器辐射声计算方法中计算时间长、实时性差、达不到作战使用要求的缺点，通过用图像欧氏距离进行传感器证据生成，以及一种改进的D－S证据合成方法相结合，提出了一种新的水下航行器声隐身性能快速评估方法。并利用仿真和实验相结合的方式，比较了本文方法和传统方法的差异。该评估方法计算速度较快、评估正确率较高、通用性较强，可应用于各类结构的声学状态评估，一定程度上为作战使用提供了技术支持。

然而该方法还需进一步改进的地方:对于不同位置的传感器，其评估正确率差别都相当大。所以在使用中，需要结合实际航行器结构进行传感器安装位置的研究;对于已安装好传感器的航行器，在选用传感器时还需要进行筛选，尽量用少的传感器信息得到较高的评估正确率，从而满足实时性和有效性的平衡。

［1］汤智胤，姜荣俊，何 琳.潜艇声隐身态势评估方法研究［J］.武汉理工大学学报(交通科学与工程版)，2007，31(1):17－20.

［2］彭 旭，骆东平.船舶结构建模及水下振动和辐射噪声预报［J］.噪声与振动控制，2003，23(6):9－12.

［3］伍先俊，朱石坚.统计能量法及其在船舶声振预测中的应用综述［J］.武汉理工大学学报(交通科学与工程版)，2004，28(2):212－215.

［4］姚德源，王其政.统计能量分析原理及其应用［M］.北京:北京理工大学出版社，1995，175(4－5).

［5］Wang L，Zhang Y，Feng J.On the euclidean distance of images［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(8):1334－1339.

［6］封举富，王立威.图像空间中的距离［M］.北京:清华大学出版社，2007.

［7］杨晓明，谭永红，苏密勇.D－S证据理论合成规则的一些修正［J］桂林电子工业学院学报，2004，24(1):13－16.

［8］Zadeh L A.Review of Shafer＇s A Mathematical Theory of Evidence［J］，AI Magazine，1984，5:81 －83.

［9］Yager R.On the Dempster Shafer framework and new combination rules ［J］. InformationSciences，1987(41):93－137.

［10］Jousselme A L ，Grenier D，Bossé E.A new distance between two bodies of evidence［J］.Information Fusion，2001(2):91－101.

［11］杜 锋，施文康，邓 勇.证据特征提取及其在证据理论改进中的应用［J］.上海交通大学学报(增刊)，2004(38):164－168.