弹性飞机的混合H2/H∞最优PID控制器参数优化

章 萌 ， 李爱军 ， 刘世民

(1.鲁东大学 电子与电气工程学院，烟台 264025;2.西北工业大学 自动化学院，西安710072;3.中航工业第一飞机设计研究院第6研究所，西安 710089)

现代大型飞机具有轻结构质量、薄升力面、细长机身和低动压载荷系数等的特点，这使得飞机的结构柔性增加，结构弹性形变增大，因此，需要考虑结构弹性形变的影响，这种考虑了结构弹性形变的飞机称为弹性飞机。由于弹性飞机的弹性运动与刚性运动之间会出现较强的耦合，传统的针对刚性和弹性模态分别设计控制器的方法变得不再适用［1］。另外弹性飞机在建模时在刚性模态的基础上引入了大量的弹性自由度来表示弹性模态，刚性模态和弹性模态的耦合与叠加使得弹性飞机模型往往具有很高的阶次。如果直接基于其全阶模型进行控制器设计往往会带来复杂的设计过程和大量的运算工作，得到的控制器阶次往往也很高，不利于工程的实现。因此，基于弹性飞机的降价模型进行控制器设计是一种较好的选择，但由于降阶模型与全阶模型之间必然存在着降阶误差(非参数不确定性或高频未建模动态)，这又需要设计鲁棒控制器来镇定模型降阶带来的非参数不确定性。

对于弹性飞机鲁棒控制器的设计，文献［2－4］和文献［5］分别使用H∞混合灵敏度控制方法和QFT方法基于降阶模型设计了鲁棒控制器。这些鲁棒控制器虽然具有一定的鲁棒性，但也存在着控制器阶次较高、增益较大等缺点，这些缺点显然不利于控制器的工程实现。因此，在弹性飞机的鲁棒控制器设计中迫切需要一种既能保证鲁棒性又能降低控制器阶次和增益的方法。

文献［6－7］提出的混合H2/H∞最优PID控制器设计方法是一种鲁棒优化设计方法，该方法结合了鲁棒控制、PID控制和智能优化算法的各自优点，把系统H2/H∞范数作为优化设计指标，使用遗传算法(GA)作为优化工具来进行PID控制器参数优化，从而获得鲁棒性较强且控制器阶次较低的鲁棒最优PID控制器。文献［8］研究了F18/HARV飞机的混合 H2/H∞最优PID控制器的参数优化，得到的控制器阶次较低且具有较强的鲁棒性能，表明了该优化设计方法设计的控制器既有较强的鲁棒性又有控制器结构简单、阶次和增益较低等优点，因此，完全可以把该优化设计方法用于弹性飞机中，但目前对于该问题的研究成果还没有。

差分进化算法(DE Algorithm)是由Storn R和Price K提出的一种群智能优化算法［9］。该算法实际上是一种实数编码且基于贪婪保优策略的遗传算法，具有算法原理简单、易于实现、优化性能强等优点，已经在优化领域得到了广泛应用。因此，完全可以代替遗传算法用于混合H2/H∞最优PID控制器的参数优化中。

为此，本文研究了弹性飞机的混合H2/H∞最优PID控制器的参数优化。首先，基于平衡截断法得到了某弹性飞机的降阶模型，并根据降阶模型与全阶模型的降阶误差选取了合适的鲁棒加权函数。之后，给出了一种计算闭环系统误差H2范数的简化计算方法，从而可以计算H2/H∞优化设计指标。最后，使用DE算法对混合H2/H∞最优PID控制器参数进行参数优化。

1 混合H2/H∞PID控制器优化设计的基本原理

1.1 优化设计指标

考虑如图1所示的鲁棒PID控制系统，PID控制器的形式为:

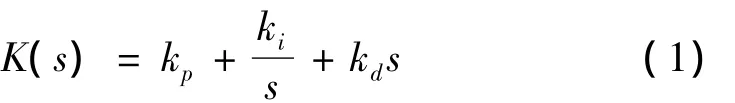
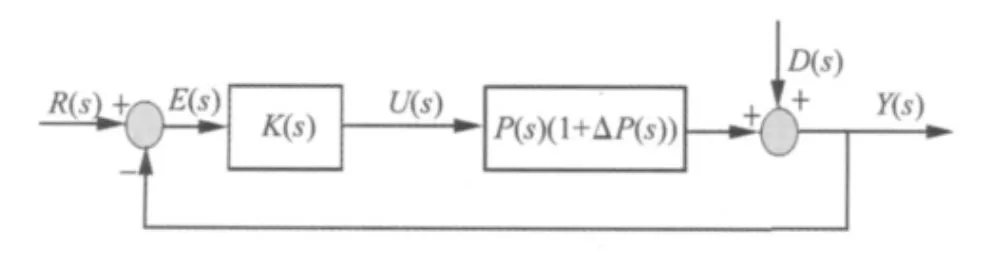
图1 鲁棒PID控制系统Fig.1 Robust PID control system

被控对象P(s)中含有乘性不确定性摄动ΔP(s)，其中:ΔP(s)假定为稳定的但具体形式并不确定的一个不确定性集，通过一个已知稳定的加权函数WT(s)来限定其摄动范围，即满足:或者(ΔP(jω))＜(WT(jω))。

假定ΔP(s)=0，则系统的灵敏度函数S和补灵敏度函数T可分别定义为:

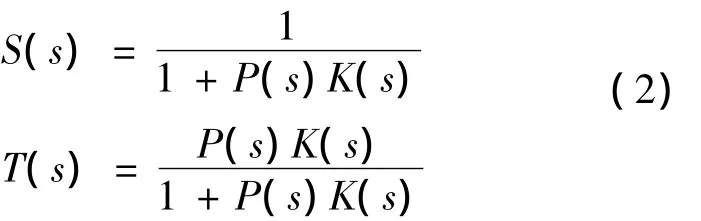
灵敏度函数S(s)是误差E(s)与参考输入R(s)之间的传递函数，是决定系统跟踪误差大小的最重要指标。S(s)的奇异值越小，则系统的跟踪误差越小，系统的跟踪性能越好。同时，S(s)也是干扰D(s)与输出Y(s)之间的闭环传递函数，S(s)的奇异值越小，系统对干扰的抑制能力就越强。因此，可以用作为闭环系统对干扰抑制能力和跟踪能力的度量。在此引入灵敏度函数加权函数Ws(s)，使其满足:

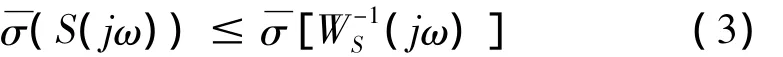
补灵敏度函数T(s)是系统参考输入R(s)与输出Y(s)之间的闭环传递函数矩阵，它是决定系统鲁棒稳定性的重要指标，在系统存在不确定性时，有较大的加权会迫使系统的输出信号稳定。T(s)的奇异值越小，标志着系统因模型不确定性产生的复合干扰对系统的影响越小，因此是对乘性摄动(1+ΔP(s))鲁棒性的一种测度。在此，引入补灵敏度函数加权函数WT(s)，使其满足:

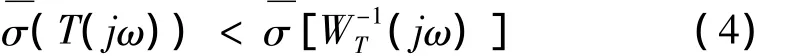
为了使系统同时获得良好的干扰抑制能力、跟踪能力和鲁棒稳定性，希望控制系统的灵敏度函数S(s)和补灵敏度函数T(s)的奇异值能够同时达到最小，但由式(2)可知S(s)+T(s)=1，二者同时最小是相互矛盾的。这就需要对灵敏度函数S(s)和补灵敏度函数T(s)在特定频段内进行折衷处理，使得在低频段内系统的灵敏度函数的奇异值较小，在高频段内系统的补灵敏度函数的奇异值较小。引入加权函数WS(s)和WT(s)后，使它们分别在低频段和高频段上具有较大的值，则可以引出如下两个H∞优化设计指标:

①鲁棒稳定性指标:

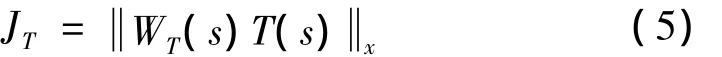
②干扰抑制指标:

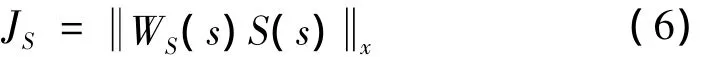
对二者进行折衷处理得到总的H∞优化指标为:

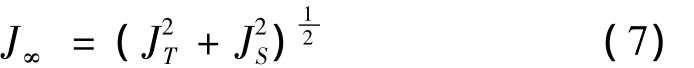
为最小化闭环系统的跟踪误差，引入闭环系统跟踪误差E(s)的H2范数指标:

混合H2/H∞最优PID控制器优化设计的最终优化指标J为:

由上可得混合H2/H∞最优PID控制器优化设计的要求是:优化设计一个PID控制器，在保证名义闭环系统(ΔP(s)=0，D(s)=0)稳定的情况下，使得式(9)所示的系统H2/H∞范数优化指标最小。

1.2 闭环系统误差E(s)的H2范数的计算方法

对于闭环系统误差E(s)的H2范数的计算方法，文献［10］给出了一个初步的结果，但计算过程较为繁琐复杂，下面给出一个简化的计算方法。

闭环系统的跟踪误差E(s)为:

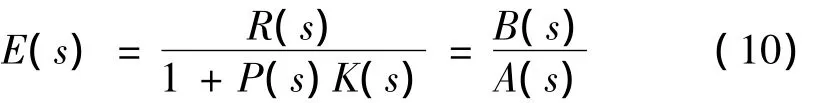
其中:R(s)为单位阶跃信号。

根据Parseval定理有:

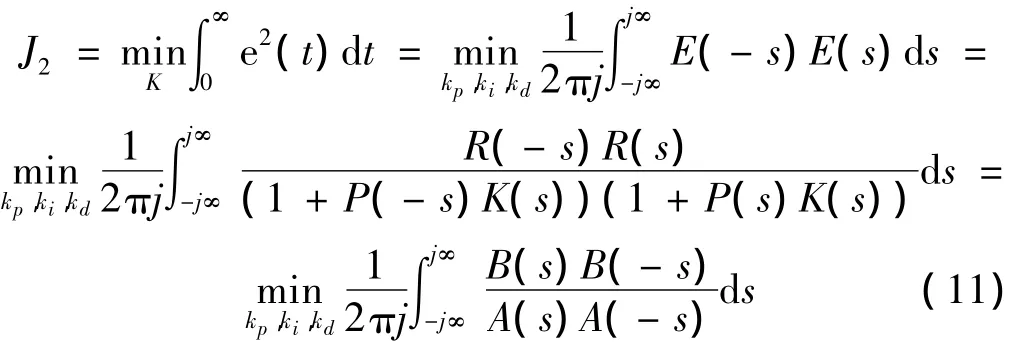
其中:A(s)，B(s)是Hurwitz多项式。

上述优化问题可以借助于留数定理来解决。

假定:

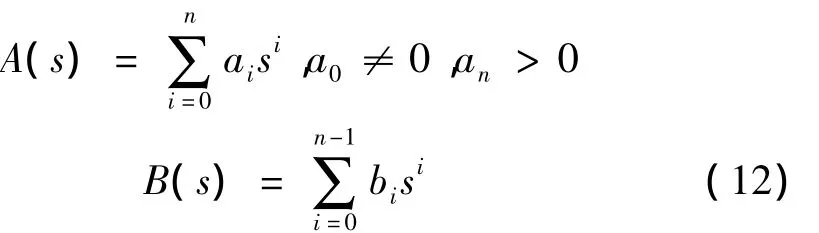
根据式(12)可以把式(11)表示为:

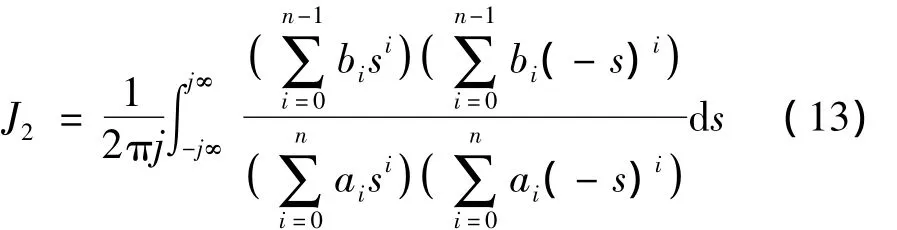
则有［10］:

其中:Pn－1是下面求解 Pi(i=0，1，…，n －1)的 n 个方程得到的结果:

同时令:

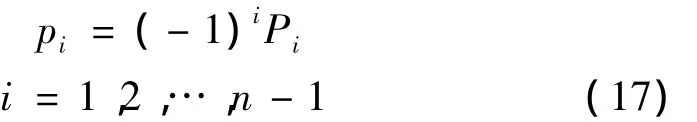
且 P=［p0，p1，…，pn－1］T。

则式(15)可以写为矩阵方程

其中Ω为矩阵:

为了求解式(18)中的pn－1，使用Cramer法则有:

其中:

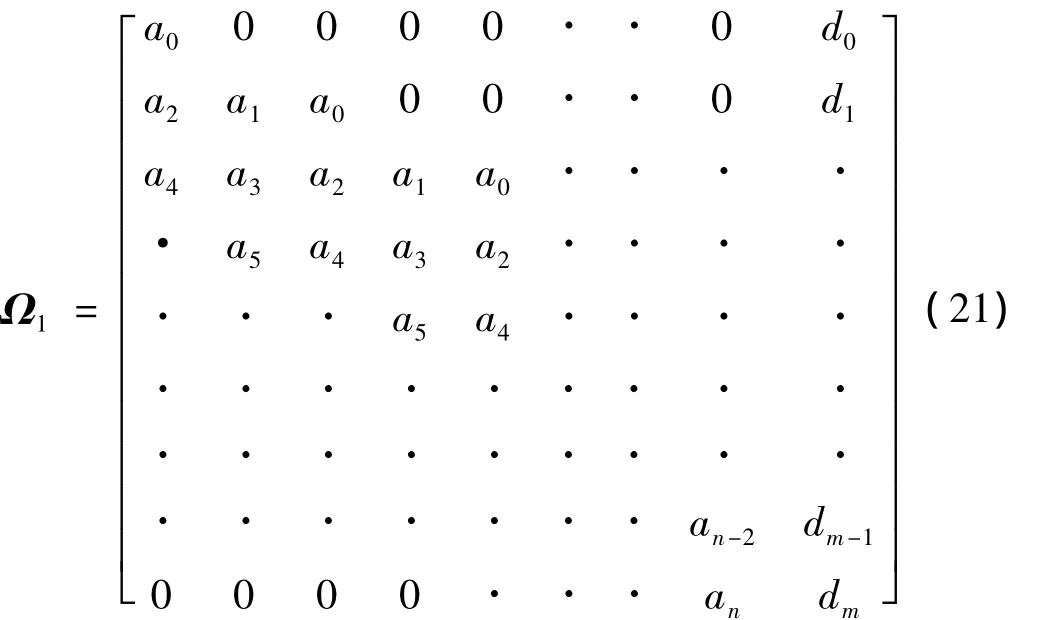
综上所述，由式(14)、式(17)和式(20)可得:

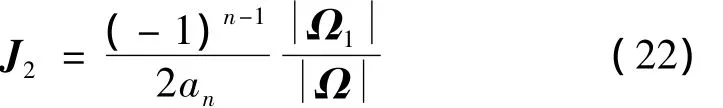
2 弹性飞机混合H2/H∞最优PID控制器参数优化

以某弹性飞机纵向运动作为例，其基准飞行状态为高度H=1500 m，马赫数M=0.6，在此状态下进行线性化处理并考虑前4阶弹性形变模态，得到该弹性飞机的全阶状态方程为:

其中:状态 x=［V，α，θ，q，ηi，i］T，ηi，i分别表示广义弹性形变及其形变速度量，i=1，2，3，4分别代表第1～4个弹性模态，其阻尼比都为ξ=0.02，自然频率分别为:ω =5.88，10.8，11，0，13.3 rad/s;V 为飞机前向速度，α是迎角，θ是俯仰角，q是俯仰角速度，输入u=δe是升降舵偏转角，输出y是驾驶舱处的法向过载n。由此可看出，该弹性飞机全阶模型各包含了4个刚性模态量和弹性模态量，由于每个弹性模态量又包含了弹性形变量和形变速度量，因此，该弹性飞机全阶模型的阶次为12阶。

2.1 模型降阶与加权函数的选取

该弹性飞机模型的Hankel奇异值如图2所示，可以看出，后6阶的 Hankel奇异值相对于前6阶的 Hankel奇异值都很小，即有:，应该可以完全截断而不会对模型的精确度产生较大影响。因此，截断后6个状态量，则降阶模型的阶次为6。

使用平衡截断算法［11，12］进行模型降阶，得到6阶降阶模型Gr(s)。图3为全阶模型和降阶模型的频域响应，从图中可以看出，中低频段降阶模型与全阶模型逼近效果较好，高频段存在一定的截断误差。在设计混合H2/H∞最优PID控制器时，就可以把模型降阶误差作为被控对象存在的非参数乘性不确定性(高频未建模动态)来处理。在选取补灵敏度加权函数WT(s)时应使其覆盖Δm(s)所包括的乘性不确定区域。在此，选定补灵敏度加权函数为WT，则乘性不确定性Δ(s)和补灵m

敏度加权函数WT(s)的频率响应曲线如图4所示。此外，选取灵敏度加权函数为:

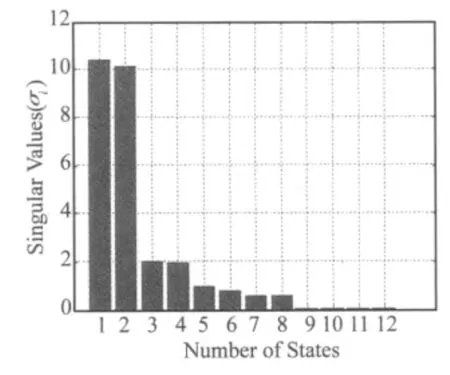
图2 弹性飞机全阶模型的Hankel奇异值Fig.2 Flexible aircraft full order model Hankel singular values

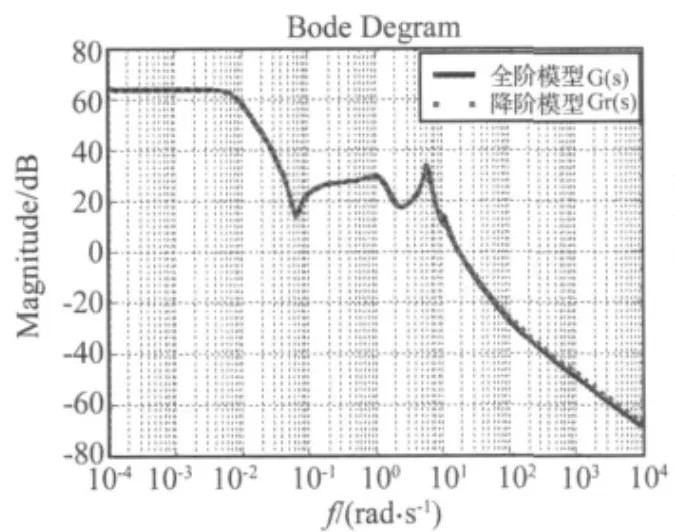
图3 全阶模型与降阶模型的频率响应Fig.3 Full order model and reduced order model frequency responses

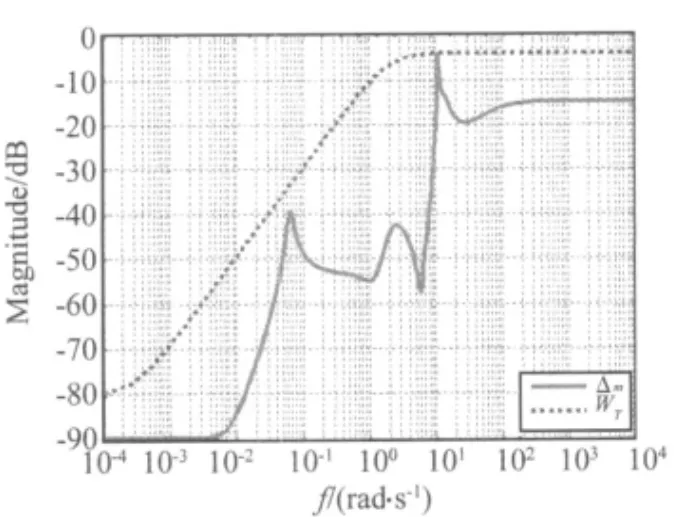
图4 乘性不确定性和补灵敏度加权函数的频率响应Fig.4 Multiplicative uncertainty and complementary sensitivity function frequency responses

2.2 闭环系统误差E(s)的H2范数的计算

对如图1所示的鲁棒PID控制系统，闭环系统误差的传递函数为:

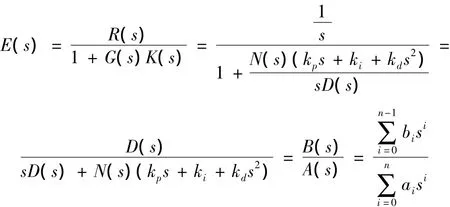
根据式(16)、式(19)、式(21)可得:

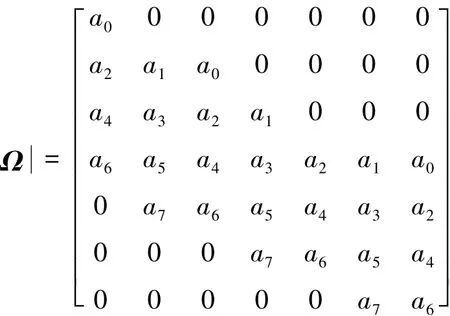
则由式(22)可得闭环系统误差E(s)的H2范数的计算公式为:

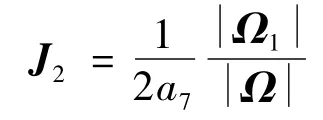
2.3 基于DE算法的最优PID控制器参数优化

把式(9)所示的优化指标作为优化设计中的目标函数，使用DE算法优化混合H2/H∞最优PID控制器的参数。首先对待优化参数kp、ki和kd进行编码，个体编码结构为:x=［kp，ki，kd］，则形成了一个 3 维的搜索空间。随机初始化m=30个个体形成一群初始随机解，其中第 i个个体为 xi=(xi1，xi2，xi3)，i=1，2，…，m。xi的搜索范围为 xi∈［0，20］。

按照差分进化算法的要求，由式(24)对个体进行差分变异操作得到变异个体vi。

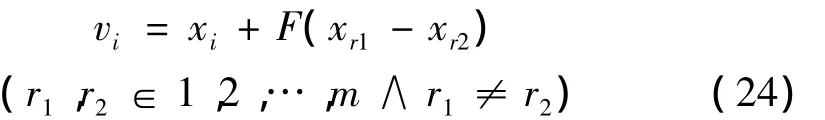
其中:F为缩放因子，选取为F=0.5。

然后对个体xi和变异个体vi进行交叉操作得到试验个体ui，其第j个染色体可表示为:

其中:rand(0，1)为［0，1］之间的均匀随机数;jrand为［1，3］之间的生成的随机整数;CR为交叉概率因子，选取为 CR=0.3。

最后，进行选择操作，得到如式(26)所示的下一代个体 xi'。

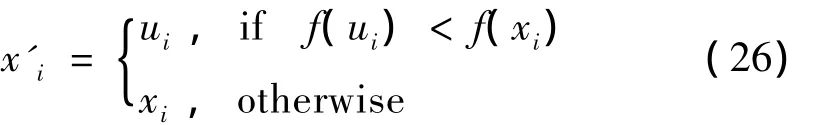
其中:f(·)为适应度函数，即为如式(9)所示的优化指标。

经过50次迭代后，得到的混合H2/H∞最优PID控制器参数为:

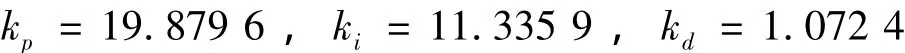
3 鲁棒稳定性验证与仿真分析

3.1 鲁棒稳定性验证

基于降阶模型设计了混合H2/H∞最优PID控制器，但要使用该控制器控制弹性飞机全阶模型，设计的控制器是否具有较强的鲁棒性来镇定模型降阶产生的非参数乘性不确定性从而保证整个系统的鲁棒稳定性是首先需要验证的。

对于非参数乘性不确定性Δm(s)，有G(s)=［I+Δm(s)］Gr(s)，根据小增益定理，如果则系统具有鲁棒稳定性。

图5 给出了 σ［Δm(jω)］和 σ［T－1(jω)］频率响应鲁棒稳定性验证曲线，可以看出，在全频段内都满足小增益定理，设计的控制器能够保证系统的鲁棒稳定性。

3.2 仿真分析与比较

为体现出优化设计的混合H2/H∞最优PID控制器的优越性，现将其与H∞混合灵敏度控制器的控制效果和鲁棒性能做比较。在进行H∞混合灵敏度控制器的设计时，所选的加权函数与混合H2/H∞最优PID控制器设计中选取的加权函数完全一致，设计得到的H∞混合灵敏度控制器为:

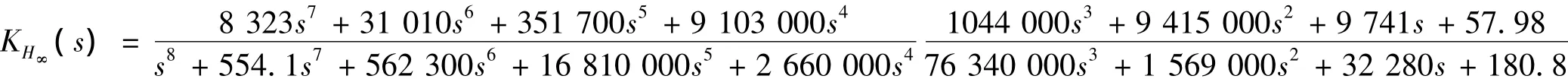
分别使用混合H2/H∞最优PID控制器和H∞混合灵敏度控制器控制弹性飞机的全阶模型，其状态方程如式(23)所示，输入信号为单位阶跃信号，输出量为过载和弹性模态的形变量和形变速度量，因为在模型降阶时截断了后3个弹性模态，因此，我们重点关注后3个弹性模态的响应情况。过载和后3个弹性模态的时域响应如图6、图7所示。

由以上仿真图可看出，在标称状态时，两种控制器的控制效果较相近，H∞混合灵敏度控制器作用下的过载响应无稳态误差和超调量，混合 H2/H∞最优 PID控制器作用下的过载响应无稳态误差，超调量为2.5%，调节时间都为3.5 s。但设计的混合 H2/H∞最优PID控制器的阶次和增益远小于H∞混合灵敏度控制器。

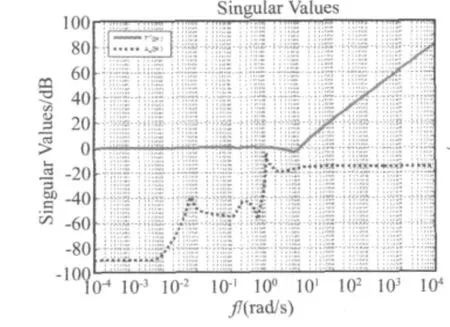
图5 鲁棒稳定性验证曲线Fig.5 Robust stability validation curve

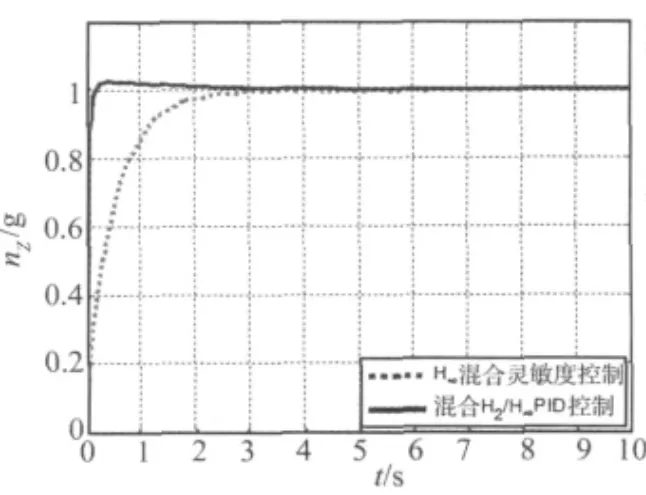
图6 过载响应曲线Fig.6 Overload response curve

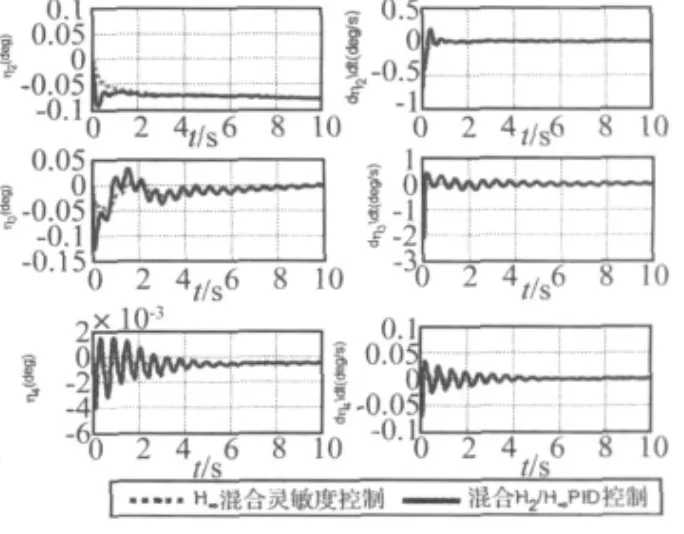
图7 弹性模态的响应曲线Fig.7 Elastic modal response curve

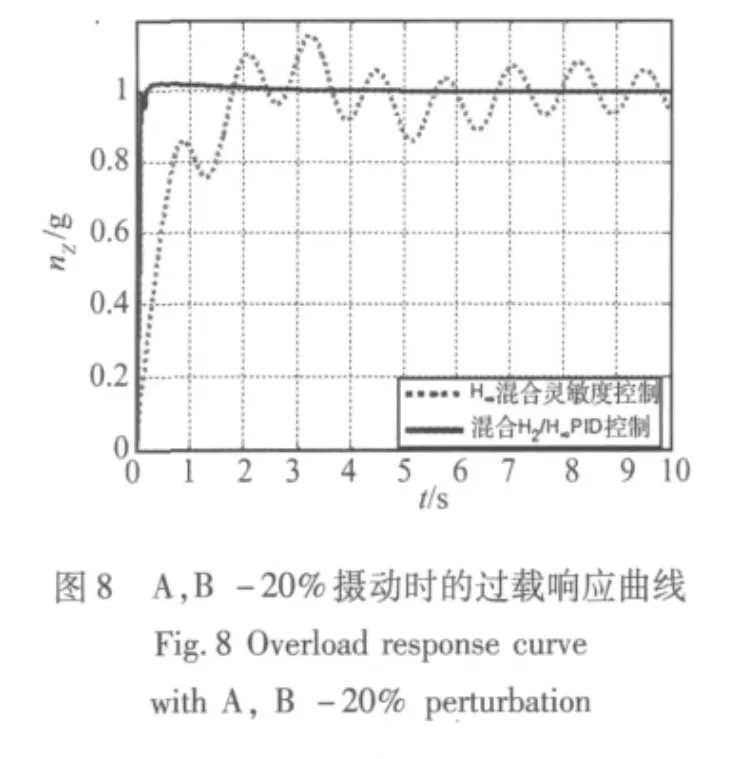
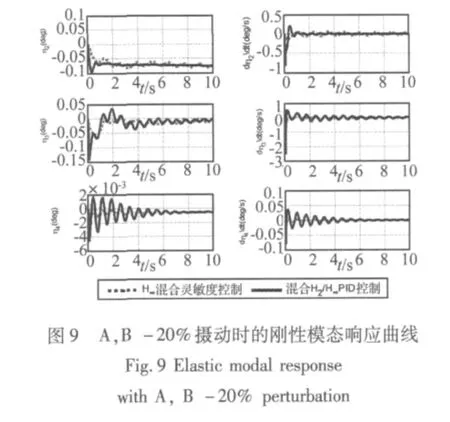
当弹性飞机全阶模型的状态矩阵和控制矩阵A，B存在－20%摄动时，即被控系统同时存在着参数不确定性和非参数不确定性时，弹性飞机的过载和后3个弹性模态的时域响应如图8、图9所示。

由以上仿真图可看出，此时H∞混合灵敏度控制器不能对弹性飞机进行较好地控制，特别是过载和第2个弹性模态的响应呈现出明显的振荡发散的趋势，表明该控制器仅能镇定非参数不确定性这一种不确定性。而混合H2/H∞最优PID控制器却能取得较好的控制效果，过载响应无稳态误差，超调量为2.5%，调节时间约为3.8 s。同时，各个弹性模态都能够得到较好地抑制，快速地衰减到零。此时的响应与标称时的响应十分接近，这表明该控制器能够同时镇定参数和非参数两种不确定性，具有更强的鲁棒性。

通过以上分析比较可知，经过参数优化后得到的混合H2/H∞最优PID控制器与传统的H∞混合灵敏度控制器相比，具有控制器阶次低、增益低、鲁棒性强等优点。

4 结论

本文研究了弹性飞机混合H2/H∞最优PID控制器的参数优化问题。通过使用差分进化算法极小化H2/H∞优化指标优化了混合H2/H∞最优PID控制器的参数，使得控制器具有较强的鲁棒性和较低的增益。仿真结果表明，优化设计的混合H2/H∞最优PID控制器可以同时镇定参数和非参数两种不确定性，具有更强的鲁棒性。表明该参数优化方法是弹性飞机混合H2/H∞最优PID控制器参数优化中一种有效、实用的方法。

［1］Schmidt D K，Raney D L.Modeling and simulation of flexible flight vehicles ［J］.Journal of Guidance，Control and Dynamics，2001，24(3):225 －235.

［2］Li X H，Ramesh K A.Application of reduced-order-models to robust control of the dynamics of a flexible aircraft［R］.AIAA－2003－5504，2003.

［3］刘世民.弹性飞机模型降阶与控制律设计［D］.西安:西北工业大学，2010.

［4］刘 宝.弹性飞机的建模与控制研究［D］.西安:西北工业大学，2008.

［5］李爱军，章卫国，刘世民，等.基于降阶模型的弹性飞行器QFT控制设计与仿真［C］//中国航空学会.第三届中国导航、制导与控制学术会议论文集.北京:航空工业出版社，2009.396－400.

［6］Chen B S，Cheng Y M.A genetic approach to mixed H2/H∞optimal PID controller［J］.IEEE Control System Magazine，1995，15(5):51 －60.

［7］Renato A K，Joost P R.Design of optimal disturbance rejection PID controllers using genetic algorithm ［J］.IEEE Trans on Evolutionary Computation，2001，5(1):78 －82.

［8］Ho S J，Ho S Y，Hung M H，et al.Designing structurespecified mixed optimal H2/H∞controllers using an intelligent genetic algorithm IGA ［J］.IEEE Trans on Control Systems Technology，2005，13(6):1119 －1124.

［9］Storn R，PriceK.Differential evolution:A simple and efficient heuristic for global optimization over continuous spaces［J］.Journal of Global Optimization，1997，11(4):341－359.

［10］Jury E，Dewey A.A general formulation of the total square integrals forcontinuoussystem ［J］. IEEE Transon Automatic Control，1965，10(1):119 －120.

［11］Moore B C.Principal component analysis in linear system:controllability，observability and model reduction［J］.IEEE Trans on Automatic Control，1981，26(1):17 －31.

［12］Laub A J，Heath M T，Paige C C，et al.Computation of balancing transformations and other applications of simultaneous diagonalization algorithms［J］.IEEE Trans on Automatic Control，1987，32(2):115 －122.

［13］胡 峰，吴 波，胡友民，等.利用粒子群优化算法实现阻尼比和频率的精确识别［J］.振动与冲击，2009，28:(7):8－11.