模糊信息分配法在裂隙结构面特征统计中的应用

董贵明，束龙仓，王茂枚，刘丽红，陶玉飞

(1. 中国矿业大学 资源与地球科学学院，江苏 徐州，221116；2. 河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京，210098；3. 江苏省水利科学研究院，江苏 南京，210017；4. 北京木联能软件技术有限公司，北京，100085)

岩体裂隙结构面特征包括产状、间距、组数、延续性、粗糙度、张开度、充填情况和连通性等，通过野外调查、绘制各种裂隙统计图和数理统计方法可进行结构面特征的分析。结构面特征分析是岩体渗流分析、岩体工程设计和稳定性分析的基础。常用的裂隙统计图主要包括玫瑰花图、极点图和等值线图，裂隙统计图主要反映了结构面的产状特征，可以用来对结构面进行分组，一些学者对这种方法的不足和改进进行了分析[1-2]。裂隙统计图实质上是对结构面的产状分区间统计，并以图形的形式表现出来。玫瑰花图是在一维区间上进行统计，极点图和等值线图是在二维区间上进行统计，通过这种分区间统计来提取结构面样本的信息。这里的区间是确定性区间，在确定性区间上统计时，把该区间上的样本同等对待，不考虑样本在区间的位置，会出现一定程度的信息丢失，统计结果对区间界限依赖较大，在区间附近的数据稍有波动，便进入不同的区间，导致统计结果具有一定的不稳定性[3-5]。使用离散网络模型进行岩体渗流计算时需要结构面特征的概率密度函数，该函数直接影响计算结果的准确性[6]。概率密度函数的确定方法较多，如频率直方图法、适线法、蒙特卡罗法、假设检验法等。其中频率直方图法仍然是使用较广泛的一种方法，但频率直方图中使用确定性区间进行统计，同样没有考虑样本的位置信息，结果受样本的波动影响较大，导致经验频率曲线与实际的概率密度曲线误差增加。野外调查时获得的结构面样本是有限的，有些情况下甚至是小样本数据，这时使用确定性区间进行统计时会增加信息丢失的程度，降低结果的稳定性。确定性区间上的信息统计特点是经典集合论中元素与集合非此即彼的关系引起的，模糊集合通过隶属函数建立元素与集合的关系。模糊信息分配采用了模糊区间，考虑了样本在区间中的位置信息，减弱了对区间界限的依赖程度，统计结果稳定[7-10]。模糊信息分配方法在自然灾害风险评价、气象数据分析、工业生产、人工智能、投资管理、环境评价等方面都已有应用[5]。模糊信息分配结果可以用图形来表达，也可以直接使用模糊信息矩阵。本文作者将阐述该方法进行裂隙结构面特征分析的原理、步骤，并结合具体实例进行分析。

1 模糊信息分配原理

使用模糊信息分配法分析样本信息时，首先把问题中涉及到的每个论域用模糊区间的并集表示，模糊区间由中心数和模糊度组成，对于只有一个论域的问题，这时的模糊空间是大于一维的；然后，根据信息分配公式计算每个样本对论域模糊空间中的每个模糊区间的信息量；最后，可根据模糊空间中的每个模糊区间的信息量值进行分析。一维模糊空间的信息量分布情况可以用直方图的形式表现，二维模糊空间的信息量分布情况可以用模糊信息矩阵的形式表现。可见：直方图和信息矩阵都可以用来展示样本的信息结构。裂隙结构面产状玫瑰花图只涉及到一个角度论域，极点图和等值线图涉及到2个角度论域。其他的结构面特征(比如结构面间距)涉及到的论域一般也不会超过2个。所以，本文只介绍一维、二维模糊信息分配公式及模糊信息矩阵。

1.1 一维信息分配公式

最简单的模糊区间是对称三角模糊数，其隶属函数为[5]。

式中：x0和Δ分别是论域I中某个模糊区间的中心数和模糊度；u为任意实数。这个隶属函数μI(u)也是一维模糊空间经常使用的线性模糊信息分配公式，相应的μI(u)也是实数u在以x0为中心数和以Δ为模糊度的模糊区间的信息量值。u距离中心数x0越近，信息量越大，当u取中心点时，信息量取最大值1；u距离中心数x0越远，信息量越小，当u与x0的距离大于等于模糊度时，信息量取最小值为 0。对所有的样本通过式(1)可计算出每个模糊区间总的信息量值。

1.2 二维信息分配公式

二维模糊空间是由2个一维模糊空间中的模糊区间的迪卡尔积形成的。式(2)为二维信息分配公式[5]。式中：(xi，yi)为样本；Aj和 Bk为一维模糊空间；uj和hx分别为Aj中的一个模糊区间的中心数和模糊度；vk和hy分别为Bk中的一个模糊区间的中心数和模糊度。当(xi，yi)与(uj，vk)的距离变小时，相应的信息量增加，信息量最大值为1；当(xi，yi)与(uj，vk)的距离变大时，相应的信息量变小，信息量最小值为 0。对所有的样本通过式(2)可计算出每个二维模糊区间总的信息量。

1.3 模糊信息矩阵

文献[5]中的模糊信息矩阵定义是针对输入和输出2个论域的，其实，模糊信息矩阵的2个论域不一定是输入和输出关系，如一个论域是倾向，另一个论域是倾角，同样可以根据样本得到模糊信息矩阵，但倾向和倾角并没有明显的输入、输出关系。模糊信息矩阵的形式和一般矩阵是一样的，矩阵的元素值是相应的二维模糊区间的总信息量，信息量根据式(2)计算。相应地，传统的非此即彼的信息分配方式下可以得到简单信息矩阵，矩阵的元素值是属于该二维确定性区间的样本个数。

2 模糊信息分配法在裂隙图绘制和概率密度函数估计中的应用

2.1 裂隙玫瑰花图

玫瑰花图的论域为0~360°，首先把其分成若干个大小相同的模糊区间，模糊区间的模糊度一般可取10°和20°，这与传统的统计区间长度一致。如分成36个模糊区间，那么，每个模糊区间的模糊度是 10°，每个模糊区间的中间数相差10°，第1个模糊区间的中心数是 5°，对于走向玫瑰花图只使用其中的 18个模糊区间就可以了，对于倾向玫瑰花图一般要使用全部的模糊区间。玫瑰花图的模糊区间的并集形成了一维模糊空间，根据式(1)就可以计算样本在不同的模糊区间的信息量，最后可得到每个模糊区间的总信息量，以某个实际长度(如1 cm)代表单位信息量，即可绘制出基于模糊信息分配的玫瑰花图。基于模糊信息分配的玫瑰花图的形式和传统的玫瑰花图是一样的，不同的是前者使用的是模糊区间的模糊信息，后者使用的是确定性区间上的简单信息。

2.2 裂隙极点和等值线图

极点图和等值线图上展示的是裂隙的倾向、倾角信息。这两个图分别涉及到 2个论域：倾向论域为0~360°，倾角论域为 0~90°。将每个论域分成若干个大小相同的模糊区间，计算这2个论域中的模糊区间的迪卡尔积，使用式(2)计算样本在每个二维模糊区间的信息量，根据信息量计算的结果设定一个点子代表的信息量，便可绘制出极点图、等值线图。基于模糊信息分配的极点图和等值线图在形式上与传统的极点图和等值线图是一样的，极点图、等值线图也可以直接通过二维模糊信息矩阵的形式表现出来。

2.3 结构面特征的模糊频率直方图

采用式(1)计算样本在每一个模糊区间上的信息量，模糊频率直方图的概率估计为[5]：

式中：n为样本个数；Δ为模糊度，也是各个中点数的距离；x为中心数；Qx为所有提供给以x为中心数、以Δ为模糊度的模糊区间的信息量。文献[5]，[7]，[11]和[12]中都论述了模糊频率直方图优于传统的频率直方图，其中文献[5]针对正态分布、指数分布和对数正态分布类型进行了详细的仿真实验对比。结果表明：在样本不大的情况下，模糊频率直方图估计概率比传统的频率直方图估计概率减少20%，估计精度的提高是明显的。使用式(3)可以绘制出裂隙结构面的模糊频率直方图，进而可分析其统计特征。

3 应用实例及分析

3.1 实例1

文献[13]中通过裂隙走向、倾向玫瑰花图结合裂隙类型与填充情况对某坝基岩体稳定性进行分析，裂隙调查数据见表1[13]。本文采用表1中数据进行裂隙统计的传统绘图方法与基于模糊信息分配的绘图方法的对比分析。裂隙走向、倾向玫瑰花图见图1~4。

图1 传统裂隙走向玫瑰花图Fig.1 Rose map of traditional fissure trend

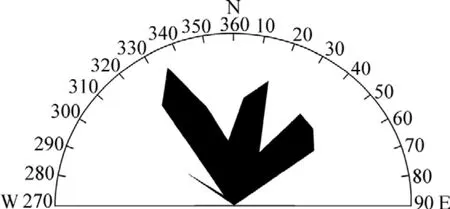
图2 基于模糊信息分配的裂隙走向玫瑰花图Fig.2 Rose map of fissure trend based on fuzzy information distribution

图3 传统裂隙倾向玫瑰花图Fig.3 Rose map of traditional fissure dip

图4 基于模糊信息分配的裂隙倾向玫瑰花图Fig.4 Rose map of fissure dip based on fuzzy information distribution

图1采用的区间长度是10°，图2中模糊区间的模糊度为10°，图3采用的区间长度是20°，图4中模糊区间的模糊度为20°。在图1和图3中有很多的“尖点”，这种情况在小样本的图形中是经常见到的，这是由于某个区间中的样本点仅仅只对该区间提供信息，是非此即彼的简单信息分配的结果，并没有考虑样本点尤其是在区间边界附近的样本点对其相邻区间提供的信息。图2和图4中，由于采用了模糊信息分配方法，这种“尖点”现象明显减弱，并且走向和倾向的分组以及优势组更加清楚。

倾向、倾角的组合信息本文使用简单信息矩阵和模糊信息矩阵反映，见表2和3。表中的数据分别为相应区间的裂隙条数和信息量，简单信息矩阵和传统的极点图是一致的。表3中非0值个数比表2中明显增加，即表2中有些是0值的地方在表3中变成了非0值，并且这些非0值中有些会相对较大，如在表2和3的左上侧范围内的数值中，表2中有3个非0值(2，3，5)，在倾向[40,60)与倾角[10,20)处数值是 0，但在表3中该位置变成了2.04，在周围的6个非0数值中是第2大的数。这是因为从表1中可以看到有很多样本点在区间[40,60)∪[10,20)边界附近，这些样本点可以对该区间提供一定的信息。表3中非0值个数比表2明显增加也表明了信息的过渡性增加。

表1中有些倾角刚好位于表2的区间边界上，区间的边界稍有变化；表2中的统计结果就会有较大的变化，但表3中统计结果的变化比表2中统计结果的变化小得多，这可由式(2)看出，表明模糊信息分配法统计的稳定性好于传统统计方法。另外，从传统玫瑰花图上可以得到某个统计区间的样本平均值。这个平均值在大样本下，根据中心极限定理是理论值的无偏估计所得，但实际中，一般不容易得到一个大样本尤其是某个区间上的大样本，这时，传统玫瑰花图上的某个统计区间的样本平均值没有多大意义，应该更多地关注在区间上的模糊信息量，而不是样本平均值。

表1 裂隙调查结果Table 1 Fissure survey results

表2 倾向和倾角简单信息矩阵Table 2 Matrix of dip and trend simple information

表3 倾向和倾角模糊信息矩阵Table 3 Matrix of dip and trend fuzzy information

3.2 实例2

后寨地下河流域位于贵州省普定县城以南 11 km，为典型的喀斯特流域，在该区域已进行了大量的裂隙统计工作[14]。陈旗堡地区位于后寨地下河流域的东北部，为峰丛洼地地貌，该地区已经设立气象、水文观测站及试验区，成为研究西南喀斯特地区石漠化问题的典型试验地区。地层为中三叠统关岭组的第 2段中的第1层和第2层，即 T2g2-1和 T2g2-2地层，岩层倾角为5°左右，倾向接近270°。选择该区内的3个测线，对厚层灰岩地层出露地表的溶蚀裂隙间距进行统计，该溶蚀裂隙主要有2组：第1组平均走向为301°，另一组平均走向为29°。选择第 1组进行裂隙间距的直方图特征进行分析，表4所示为第1组裂隙间距。绘制传统频率直方图和模糊频率直方图，并采用切比雪夫多项式函数逼近方法确定了概率密度函数曲线，见图5和图6。

图5 传统裂隙间距频率直方图Fig.5 Frequency histogram of traditional fissure distance

图6 裂隙间距模糊频率直方图Fig.6 Fuzzy frequency histogram of fissure distance

表4 裂隙间距Table 4 Fissure distance

图5中统计区间长度为20 cm，图6中模糊度为20 cm，第1个模糊区间的中心数为20 cm。基于切比雪夫多项式函数逼近的概率密度函数确定方法充分利用了样本的各阶矩，具有较高的精度[15-16]。模糊频率直方图比传统的频率直方图更能显示某种统计规律，并且更接近概率密度曲线，即基于模糊信息分配公式的区间信息量计算方法充分提取了样本点中的信息，信息量的计算是比较准确的。

对统计区间的长度(模糊度)、起始和结束值进行调整，可绘制出多组对比图。经对比后发现，基本上都能得到图5与图6的对比结果，对比结果并未一一列出。同时，对比结果也表明模糊频率直方图的稳定性比传统频率直方图的稳定性强。

4 结语

(1) 将模糊信息分配法应用到裂隙结构面特征的统计分析中是基于模糊信息分配公式的模糊集合在对数据的区间识别上的应用，体现了经典集合和模糊集合在对数据的区间识别上的重要区别，考虑了样本的模糊过渡信息，减小了统计结果对区间界限的依赖性，增强了结果的稳定性。

(2) 在小样本的情况下，将模糊信息分配方法应用到裂隙结构面的产状、间距分析中，得到了较好的结果，为小样本情况下进行裂隙结构面特征统计分析提供了一种新的途径。在大样本情况下，没有使用实例数据进行分析，但从模糊信息分配方法的原理上可看出，模糊信息分配方法的统计结果仍优于确定性区间统计结果。结构面的其他特征和产状、间距特征具有相似性，也可以使用模糊信息分配方法进行分析。

(3) 基于模糊信息分配的结构面特征分析方法原理简单、易操作、结果合理，是一种较好的裂隙结构面特征分析方法，值得推广使用。

[1] Shanley R J, Mahtab M A. Delineation and analysis of clusters in orientation data[J]. J Math Geol, 1976, 8(3): 9-23.

[2] 范雷, 王亮清, 唐辉明. 节理岩体结构面产状的动态聚类分析[J]. 岩土力学, 2007, 28(11): 2405-2408.FAN Lei, WANG Liang-qing, TANG Hui-ming. Dynamic cluster analysis of discontinuity orientations of jointed rock mass[J]. Rock and Soil Mechanics, 2007, 28 (11): 2405-2408.

[3] LIU Zheng-rong, HUANG Chong-fu. Information distribution method relevant in fuzzy information analysis[J]. Fuzzy Sets Systems, 1990, 36(1): 67-72.

[4] 彭贵芬, 张一平, 赵宁坤. 基于信息分配理论的云南干旱风险评估[J]. 气象, 2009, 35(7): 79-86.PENG Gui-fen, ZHANG Yi-ping, ZHAO Ning-kun. Drought risk assessment in yunnan province on the basis of information distribution theory[J]. Meteorological Monthly, 2009, 35(7):79-86.

[5] 黄崇福. 自然灾害风险评价理论与实践[M]. 北京: 科学出版社, 2005: 55-60.HUANG Chong-fu. Risk assessment of natural disaster theory &practice[M]. Beijing: Science Press, 2005: 55-60.

[6] Long C S, Gilmour P, Witherspoon P A. A model for steady fluid flow in random three-dimensional networks of discshaped fractures[J]. Water Resour Res, 1985, 21(8): 1105-1153.

[7] Marti K. Coping with uncertainty[M]. New York: Springer, 2006:77-79.

[8] Hardy C C. Wildland fire hazard and risk: Problems, definitions and context[J]. Forest Ecology and Management, 2005, 211(1):73-82.

[9] Adrian C. Integrated risk and vulnerability assessment and management assisted by decision support systems[M]. Dordrecht:Springer, 2005: 80-85.

[10] 黄崇福. 自然灾害风险分析的信息矩阵方法[J]. 自然灾害学报, 2006, 15(1): 1-10.HUANG Chong-fu. Information matrix method for risk analysis of natural disaster[J]. Journal of Natural Disasters, 2006, 15(1):1-10.

[11] Megumi K, Judith M S, Hyg M S, et al. First-aid training and capabilities of the lay public: a potential alternative source of emergency medical assistance following a natural disaster[J].Disaster, 2005, 29(1): 58-74.

[12] 王新洲, 邹双朝, 邹进贵, 等. 模糊直方图及其在测量数据处理中的应用[J]. 武汉大学学报: 信息科学版, 2004, 29(5):385-388.WANG Xin-zhou, ZOU Shuang-chao, ZOU Jin-gui, et al.Fuzzy histogram and its application to surveying data processing[J]. Geomatics and Information Science of Wuhan University, 2004, 29(5): 385-388.

[13] 吴成扬. 节理倾向玫瑰花图在水利工程中的应用[J]. 黑龙江水专学报, 2004, 31(4): 57-59.WU Cheng-yang. Application of the rose diagram of the joins trend in the water resources engineering[J]. Journal of Heilongjiang Hydraulic Engineering College, 2004, 31(4):57-59.

[14] 陈洪元, 陈邦宇, 陈波. 贵州省普定后寨岩溶小流域水文特性研究[J]. 贵州地质, 2005, 22(4): 284-288.CHEN Hong-yuan, CHEN Bang-yu, CHEN Bo. Hydrographic characteristics of Houzhai Karst Small Valley, Puding, Guizhou Province[J]. Guizhou Geology, 2005, 22(4): 284-288.

[15] Deng J, Li X B, Gu G D. A distribution-free method using maximum entropy and moments for estimating probability curves of rock variables[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(3): 1-6.

[16] 张伟, 宫凤强, 李夕兵, 等. 一种推断岩体裂隙几何参数概率模型的新方法[J]. 岩石力学与工程学报, 2006, 25(S2):3703-3708.ZHANG Wei, GONG Feng-qiang, LI Xi-bing, et al. A new method of definition of probabilistic density functions of geometry parameters for rockmass fissure network[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2):3703-3708.