落石冲击作用下环形网耗能性能的理论及数值模拟研究

汪 敏，石少卿，康建功

(后勤工程学院 军事建筑工程系，重庆 401331)

1995年，由瑞士布鲁克集团首创的柔性防护技术被引入国内边坡地质灾害防治领域，通过十几年的发展，作为该项新技术载体的柔性防护系统在国内铁路、公路、水电站、矿山、市政及景区边坡防护工程中得到了广泛应用［1］。柔性防护系统包含被动柔性防护系统及主动柔性防护系统，被动柔性防护系统主要由以下几个部分组成:钢柱、消能件、拉锚绳、支撑绳及金属柔性网［2］，各构件按照一定的安装方式组合成被动防护系统，在系统中起着不同的作用。文献［3～5］对被动防护系统进行了试验研究，但是由于试验条件的限制，未对影响被动防护系统耗能性能的参数进行分析;文献［6］对铁路客运专线与公路并行区段柔性防护网预留变形空间进行了试验及数值计算，但未考虑约束条件对金属柔性网变形距离的影响;文献［7～9］对不同结构形式的金属柔性网组成的被动防护系统进行了数值模拟，对被动防护系统中的相关参数进行了分析;文献［10］对环形网中单个圆环进行了静力试验研究，对落石冲击不同约束形式下环形网的力学行为进行了试验研究，并通过自行编程对落石冲击防护网进行了数值模拟分析，对比了数值模拟分析结果与试验结果，给出了一种考虑落石冲击作用下防护网耗能特性的数值分析工具。被动防护系统中主要耗散能量的构件为金属柔性网，消能件，因此，考虑金属柔性网耗散能量的特性是非常重要的，这对于将金属柔性网较好的应用到整个被动防护系统当中，充分地发挥其耗散能量的能力具有重要的意义。尽管已有许多研究人员对被动防护系统及金属柔性网受冲击作用下的力学性能进行了数值模拟及试验研究，但从作者查阅的文献来看，目前对环形网耗能性能的理论分析及考虑约束条件对环形网耗能性能影响的相关研究并不多见。

基于上述原因，本文主要针对单个圆环耗能性能进行理论分析，同时讨论环形网耗能性能的特点，研究约束条件对环形网耗能性能的影响，为环形网耗能性能的评价及设计提供一定的参考依据。

1 单个圆环吸收能量的理论计算公式推导

为了方便与试验结果进行比较，本文建立模型1时采用与文献［10］相同的试验模型，其次考察被动防护系统的形式，将被动防护系统简化成模型2［9］，模型1、模型2长宽尺寸分别为:3.9 m、3.9 m，环形网中共包含180个圆环，简化模型如图1、2所示。计算中选取的网型为R7/3/300，即由直径为3 mm的钢丝、盘结7圈，按网孔内切圆直径300 mm编织成的环形网［11］。支撑绳选用φ18单绳，四周拉锚绳选用φ22单绳。根据布鲁克(成都)工程有限公司提供的钢丝绳破断拉力的相关参数［12］，取圆环等效截面面积为 A1=35.2 mm2，等效截面半径为r1=3.35 mm;支撑绳等效截面面积为A2=124.2 mm2，等效截面半径为r2=6.29 mm;四周拉锚绳等效截面面积为A3=171.0 mm2，等效截面半径为 r3=7.38 mm。

图3、图4分别给出了圆环在变形前及变形后的实物照片，从中可以看出，当环形网受到落石冲击作用以后，单个圆环由于受到周围四个圆环的影响，最后将被拉伸成矩形框架。取单个圆环进行分析，在圆环被拉伸成矩形框架的过程中，吸收的能量推导如下。

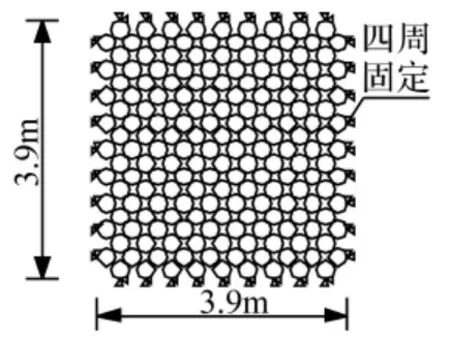
图1 模型1四周固定Fig.1 Model one fastened to its perimeter

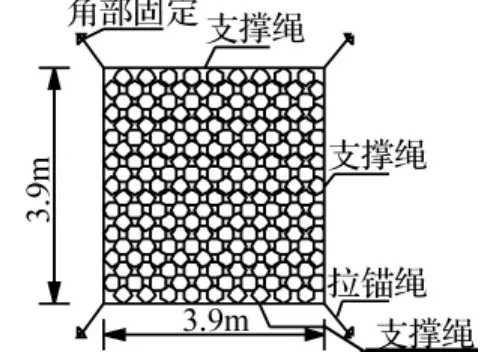
图2 模型2角部固定Fig.2 Model two fastened to its corner

图3 圆环之间的相互Fig.3 关 In系ter照rel片ation of single ring in the ring net

图4 圆环被冲击破坏后照片Fig.4 The ring net deformed after impacted

根据试验测得的ROCCO钢丝绳的本构关系［13］，将圆环的本构关系简化成弹塑性模型，应力应变关系曲线见图5所示。在理论分析中，圆环拉直成矩形框架过程中可以取1/4圆环，分成两部分进行计算。第一步，将1/4圆环拉伸成直线，第二步，将直线拉伸成直角形。第一步将1/4圆环拉伸成直线时，1/4圆环的曲率可以取为1/r，而直线的曲率为0，因此可得拉直1/4圆环耗散的能量Wa为:

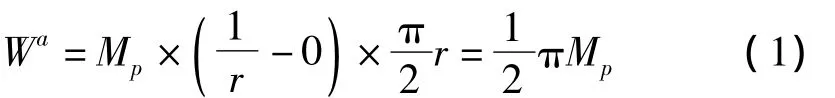
其次，求将直线拉伸成直角形时需要做的功Wb，此时:

将圆环拉伸成矩形时，需要做的总功W1为:

式中:r为圆环半径;Mp为圆环截面极限塑性弯矩，由塑性结构力学知识可求得，σ为圆环截面屈服应力，取 σ =1770 MPa，r1为圆环截面等效半径。显然，以上分析中只考虑了圆环的弯曲变形，而没有考虑圆环拉伸变形有关的能量。

根据上面理论公式的推导，将数值代入式(4)可求单个圆环弯曲变形吸收的能量为:

当圆环拉伸成矩形框架以后，圆环还可以依靠矩形框架的拉伸变形耗散能量。为了估计矩形框架在拉伸变形下的能量吸收能力，首先考虑在弯曲变形阶段所发生的拉伸应变，显然，在这个阶段严重的弯曲变形发生在塑性铰周围，根据文献［14］对塑性铰的有效长度的研究结果，本文将塑性铰的有效长度近似取为λ=12·h，其中h为弯曲元件的厚度，λ为塑性铰的有效长度。由图6可知，在弯曲变形阶段，拐角处塑性铰总的转角为(π/2)，拐角处塑性铰段中性轴的最终曲率 k，此处h=2r。注意到圆环最外层纤维1的初始曲率为1/r，发生在这一段上最外层纤维上的最大弯曲应变为。此时假定圆环的极限塑性应变为εf，而矩形框架的塑性极限轴力为NA=σA1，因此，当任一塑性铰发生拉伸失效时，四个塑性铰由于拉伸变形所耗散的总能量W2为:

图5 弹塑性应力应变关系曲线Fig.5 Assumed stress-strain curve modeling the elastic-perfectly plastic behavior of cables

图6 拐角处塑性铰区域形状Fig.6 The figure of plastic corner

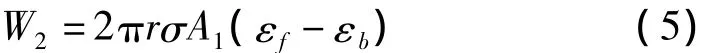
式中:εf为圆环极限塑性应变，取 εf=0.05，如图 5所示;A1为圆环等效截面面积，其余符号意义同前。根据上面理论公式的推导，将数值代入式(5)可求单个圆环被拉成矩形框架以后吸收的能量为:

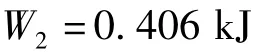
可见当圆环被拉伸成矩形框架后，圆环还有一定的耗能能力。因此，单个圆环的吸收能量的大小Wd为:

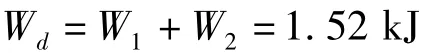
通过上面的分析，得出了单个圆环吸收的最大能量，如何评价单个圆环组成的环形网吸收的能量，对此本文作如下讨论:由于单个圆环被拉直成矩形框架以后，很快并发生破坏，经计算，W2仅仅只有弯曲耗散能量W1的36.4%，可以近似认为当环形网中所有圆环均被拉伸成矩形框架之后，环形网中圆环发生破坏，因此理想情况下模型1、模型2中环形网所能吸收的最大能量均为:

事实上，环形网吸收的能量与其约束条件有关系，如何确定合理的约束条件充分发挥环形网的最大耗能能力，下面通过数值模拟与理论相比较的方式进行研究。

2 数值模拟方法及假定

本文采用LS-DYNA软件对落石冲击环形网进行数值模拟分析，分析中选用单元:对落石的模拟选用solid164单元;对支撑绳、拉锚绳采用link160单元进行模拟，该模型只能考虑材料受到轴力的作用，不能承受弯矩，对圆环采用beam161单元进行模拟，主要考虑圆环能在拉伸过程中承受一定的弯矩［15］。

数值模拟分析时采用的材料模型:对落石采用刚性体模型，密度为2600 kg/m3，弹性模量为3.0E10，计算过程中假定落石为球体，总质量为830 kg，与文献［10］试验条件相同。对支撑绳、拉锚绳及环形网均采用塑性随动模型，该模型可以考虑单元失效及破坏效果，材料的本构关系如图5所示，密度为7850 kg/m3。泊松比为0.3。碰撞过程材料应变变化速率较大，这将对弹塑性材料的硬化行为产生较大影响，计算中采用Cowper-Symonds模型来考虑材料的塑性应变效应，用与应变率有关的因数表示屈服应力:

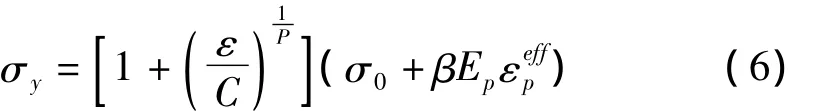
式中:σy为考虑应变率影响的屈服应力;σ0为初始屈服应力;ε，εeffp为应变率和有效塑性应变;Ep为塑性硬化模量;C，P为Cowper-Symonds应变率参数，对于钢材可分别取C=40，P=5。

在采用LS-DYNA计算落石撞击环形网时，必须满足以下假定:

(1)网中任一个构件发生破坏，即认为环形网发生了破坏;

(2) 冲击作用时间指落石与环形网开始接触到速度为0所经历的时间;

(3)对落石撞击环形网中极限速度的确定问题［9］:假设数值计算中落石速度为(vlim+1)时，模型发生了破坏，而当落石速度为vlim时，环形网没有发生破坏，此时防护网防护落石的速度为最大速度。

3 数值模拟计算结果与试验结果比较

表1中给出了文献［10］试验和本文数值模拟计算结果，落石冲击环形网的初始动能分别为45 kJ、24 kJ，本文采用LS-DYNA计算的环形网最大加速度、最大位移、冲击作用时间与试验结果吻合比较好，可见采用本文的数值模拟计算方法模拟环形网在落石冲击作用下的行为是可行的。

表2中给出了两种不同约束形式下，环形网在落石冲击极限状态下的计算结果。在模型1形式下环形网的破坏方式为圆环发生断裂，环形网被穿透，见图7所示，环形网耗能能力是理论计算值W的25%，可见模型1的约束形式严重影响环形网耗能性能的发挥;模型2形式下环形网的破坏形式为四周拉锚绳破坏，见图8所示，环形网耗能能力是理论计算值 W的59.7%，可见由于拉锚绳的强度不足，严重制约了环形网耗能性能的发挥。比较模型1、模型2两种情况，模型1发生的最大位移为模型2的73.8%，耗能能力为模型2的49.9%，可见模型2的约束形式在一定程度上能够充分发挥环形网的耗能能力。

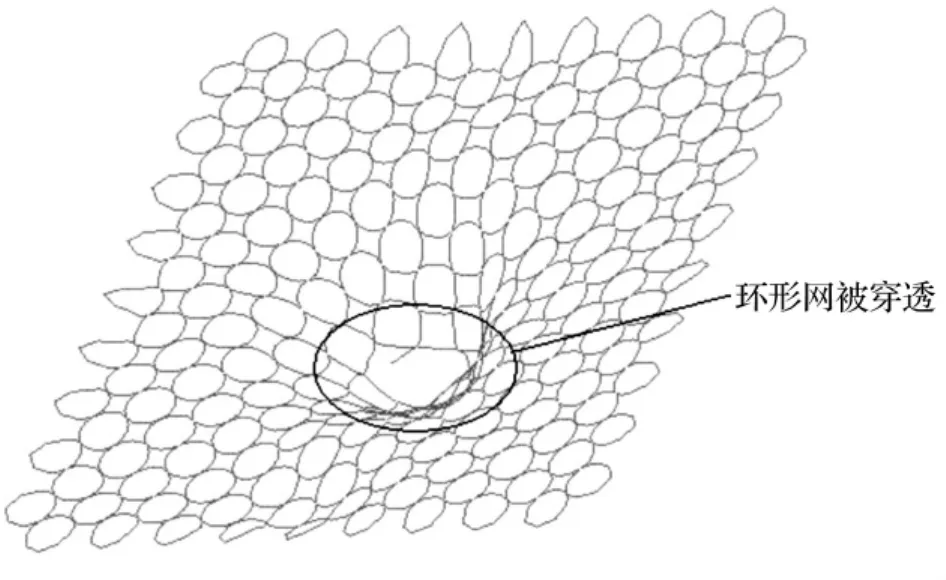
图7 模型1破坏形式Fig.7 Detail of the failure in the model 1 after impacted

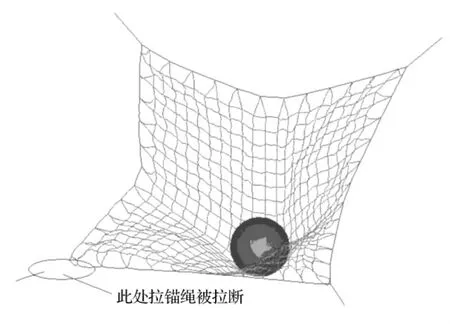
图8 模型2破坏形式Fig.8 Detail of the failure in the model 2 after impacted

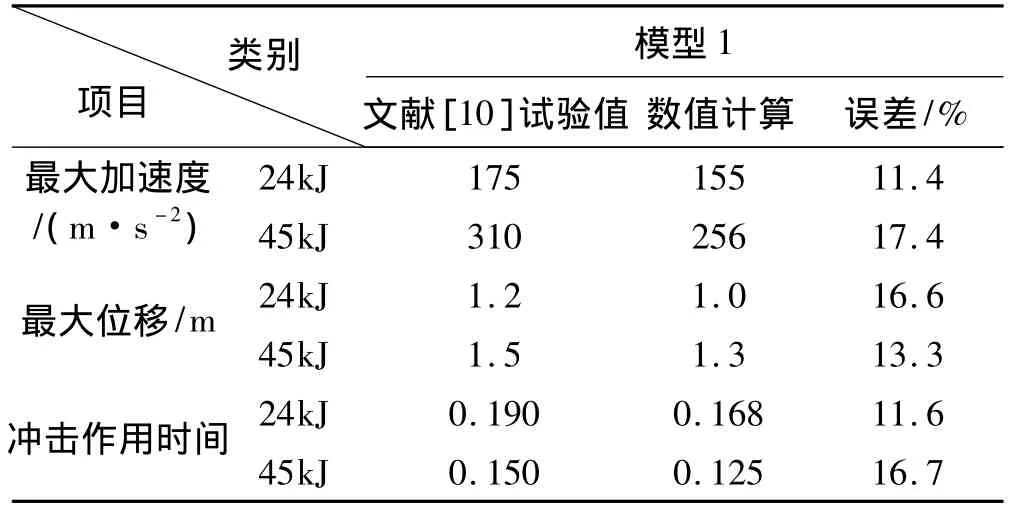
表1 模型1约束形式下环形网计算结果与试验结果比较Tab.1 Comparison between experimental and numerical results of model 1

表2 两种不同约束形式下环形网破坏时计算结果与理论结果比较Tab.2 Comparison between theory and numerical results of model 1 and model 2

4 不同约束条件下模型2耗能性能研究

对于模型2，在由支撑绳、拉锚绳、圆环构成的环形网中，若配置不当，可出现三种情形:一是个别构件能力不足而降低环形网的整体功能;二是个别构件能力过强不能充分发挥带来材料浪费;三是在约束形式一定的情况下，构件之间的相互刚度比值的影响导致环形网中圆环没有能充分发挥耗散能量的能力而带来材料浪费。为了能够充分发挥环形网耗能能力，针对模型2，着重分析环形网吸收的最大能量随拉锚绳等效截面与圆环等效截面比值之间以及支撑绳与圆环等效截面比值之间的关系，计算结果见表3、表4所示。从计算结果看出:在支撑绳不发生破坏的情况下，环形网吸收的最大能量随着拉锚绳等效截面的增大先增大后减小;在拉锚绳不发生破坏的情况下，环形网吸收的最大能量随着支撑绳等效截面的增大先增大，到一定程度后保持不变。同时，在拉锚绳等效截面与圆环等效截面比值以及支撑绳等效截面与圆环等效截面比值在适当的情况下，数值模拟计算得出的环形网吸收的最大能量为183.0 kJ，与理论预测结果 W较一致，误差为8.9%，可见理论计算公式能较好地计算环形网的最大吸收能量。

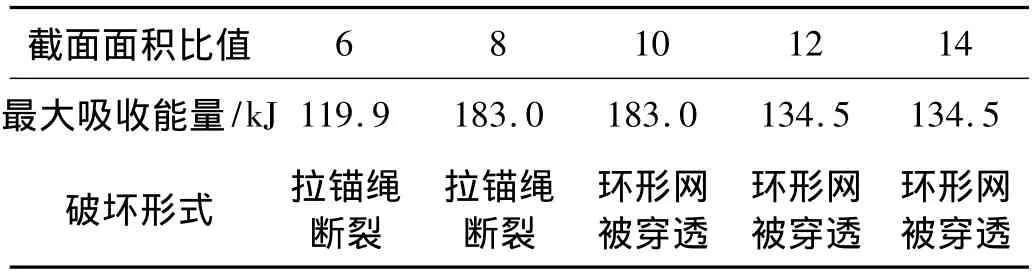
表3 拉锚绳圆环等效截面比值与环形网最大吸收能量之间的关系Tab.3 Relationship of the equivalent section between anchor rope and single ring to dissipation energy capacity of the ring net

表4 支撑绳圆环等效截面比值与环形网最大吸收能量之间的关系Tab.4 Relationship of the equivalent section between support rope and single ring to dissipation energy capacity of the ring net

5 结论

本文推导了环形网中单个圆环耗散能量的计算公式，同时将环形网的约束形式简化成模型1、模型2两种形式，讨论了环形网所能吸收的最大能力的计算方法。采用LS－DYNA软件针对环形网受到落石冲击下的力学性能进行了数值模拟分析，模型1的数值模拟分析结果与文献［10］的试验结果较吻合，为环形网受冲击作用下的力学分析提供了一种可靠的计算方法。

针对简化模型2，对影响其耗能性能的因素进行了参数分析，分析结果表明:在支撑绳不发生破坏的情况下，随着拉锚绳等效截面与圆环等效截面比值的增大，环形网吸收的最大能量先增大后减小;在拉锚绳不发生破坏的情况下，随着支撑绳等效截面与圆环等效截面比值的增大，环形网吸收的最大能量先增大，到一定程度后保持不变。在拉锚绳等效截面与圆环等效截面比值以及支撑绳等效截面与圆环等效截面比值在适当的情况下，数值模拟计算得出的环形网吸收的最大能量与理论预测结果较一致，理论计算方法能较好地预测环形网的最大吸收能量。

［1］贺咏梅，彭 伟，阳友奎.边坡柔性防护网的典型工程应用［J］.岩石力学与工程学报，2006，25(2):323－328.

［2］贺咏梅，阳友奎.SNS边坡柔性防护网的标准化问题［J］.路基工程，2002，(3):18－20.

［3］Pelia D，Pelizza S，Sassudelli F.Evaluation of behaviour of rockfall restraining nets by full scal tests［J］.Rock Mech.Rock Engng，1998，31(1):1－24.

［4］Smith D D，Duffy J D.Filed tests and evaluation of rockfall restraining nets［R］.California Department of Transportation，Final report，1990.

［5］Gottardi G，Govoni L.Full-scale modelling of falling rock protection barriers［J］.http://www.springerlink.com/content/178343x6n3t0w236/，2009.

［6］侯福国，王俊彪，禹志阳.铁路客运专线与公路并行区段柔性防护预留变形空间的研究［J］，中国铁道科学，2007，28(3):23－26.

［7］Nicot F，Cambou B，Mazzoleni G.Design of rockfall rest-raining nets from a discrete element modeling［J］.Mech.Rock Engng，2001，34(2):99－118.

［8］Bertrand D，Nicot F，Gotteland P，et al.Discrete element method numerical modeling of double-twisted hexagonal mesh［J］，Can.Geotech.J.2008，45:1104 －1117.

［9］Cazzani A，Mongiovi L，Frenez T.Dynamic finite element analysis ofinterceptive devicesforfalling rocks［J］.InternationalJournal of Rock Mechanics and Mining Sciences，2002，39:303 －321.

［10］Grassl H，Volkwein A，Anderheggen E，et al.Steel-Net Rockfall Protection Barriers http://www.wsl.ch/personalhomepages/volkwein/pdf/SUSI-RockfallProtection.pdf，2002.

［11］TB/T 3089－2004.铁路沿线斜坡柔性安全防护网［S］.北京:中华人民共和国铁道部，2004.

［12］柔性防护网(主动防护网，被动防护网)检验报告［R］.成都:布鲁克(成都)工程有限公司，2003.

［13］del Coz Diaz J J，Garcia Nieto P J，Castro Fresno D，et al.Non-linearanalysis of cable networks by FEM and experimental validation［J］.International Journal of Computer Mathematics，2009，86(2):301－313.

［14］余同希，卢国兴.材料与结构的能量吸收［M］.北京:化学工业出版社，2006.

［15］ANSYS Inc.ANSYS/LS-DANY User’s Guide［M］，2006.