随机振动功率谱再现自适应控制算法研究

关广丰，王海涛，熊 伟

(大连海事大学 机械工程系，大连 116026)

振动模拟实验的目的在于考核设备或试件在振动环境下保持其原有性能的能力，为试件的性能测试和技术改进提供实验依据。试件在工作环境中经受的振动形式大多为随机振动，振动信号的频率不局限在确定的频率点上，其特征经常用功率谱密度等统计特性描述［1］。随机振动功率谱再现实验的目的，就是在实验台上高精度再现实测的功率谱密度信号(即参考谱信号)，研究试件的结构可靠性和操纵可靠性［2］。

液压振动模拟系统负载能力大，易实现低频大位移、大推力的振动激励，常用于大型工程结构或试件的模型及实物的振动模拟试验［3，4］。但受系统频宽的限制及液压系统非线性因素的影响(如油温变化等)，仅采用伺服控制很难满足随机振动实验的精度要求。为了提高控制精度，更准确地再现参考谱信号，需要通过振动控制对驱动信号进行迭代补偿，减小响应信号的功率谱密度与参考谱信号的差别，形成一种真正意义上的振动闭环控制［5］。

传统的随机振动控制算法大多基于频响函数的离线辨识结果对驱动谱进行修正，再通过频域随机化和时域随机化方法将功率谱信号转换为时域信号，驱动平台运动［6，7］。时域随机化后生成信号的频谱存在泄漏现象，在频率分辨率之间可能产生欠试验或过试验，影响系统的控制精度。而且，由于传统控制算法为离线迭代算法，当实验过程中系统特性发生变化时，很难保证实验的控制精度。

基于自适应滤波理论辨识系统的阻抗特性，并依据实时辨识结果修正驱动信号，将有利于提高随机振动实验的控制精度。Karshenas等［8］基于快速块LMS自适应滤波算法，应用自适应逆控制技术实现了冲击波形的高精度再现。Groud等［9］应用LMS自适应滤波器设计了电动振动台随机振动控制器，并通过仿真验证了算法的有效性。

LMS算法实现简单，但收敛速度慢。基于递归最小二乘估计的RLS算法可以将自适应滤波算法的收敛速度提高一个数量级。进一步研究表明，RLS算法实际上只是Kalman滤波算法在无激励线性动态系统模型假设条件下的一种简化，基于线性动态系统状态空间模型的Kalman滤波算法更适合于进行系统辨识［10］。因此，研究基于Kalman滤波的随机振动控制算法有利于进一步提高控制算法的实时性。

本文首先提出基于滤波器设计理论的时域驱动信号生成方法，基于参考谱的信息设计FIR滤波器，通过对白噪声信号的滤波生成时域驱动信号。然后利用Kalman滤波器辨识系统的阻抗特性，基于自适应逆控制方法对激振系统的输入信号进行补偿，使得系统的响应信号能够实时再现时域驱动信号，进而实现参考谱的高精度再现。最后通过随机振动实验对算法的有效性进行验证。

1 时域驱动信号生成方法

图1所示为基于滤波器设计理论的时域驱动信号生成过程原理图。利用参考谱设计FIR滤波器，通过对白噪声信号的滤波生成时域驱动信号。

图1 时域驱动信号生成方法Fig.1 Time domain drive signal generation

定义Gdd(f)为系统输入信号功率谱密度估计值，Gcc(f)为系统响应信号自谱密度估计值，H(f)为系统的频率响应函数。由随机过程理论可知:

式中，上角标H表示复向量的共轭转置。

取驱动信号为白噪声信号，则其功率谱密度Gdd(f)可近似看为常数。设Gdd(f)=b，式(1)可简化为:

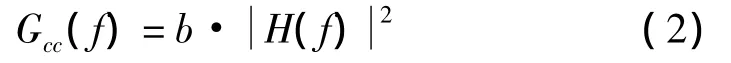
由式(2)可得:

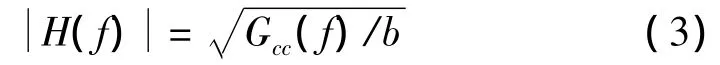
实验中，设定白噪声输入信号的功率谱密度为b，令参考谱信号为Gcc(f)，由式(3)计算所设计的FIR滤波器的幅频特性。

取线性相位φ作为FIR滤波器的相频特性，有:

式中，M为FIR滤波器的阶数。

已知滤波器的幅频特性和相频特性，基于Parks-McClellan方法，通过最小化FIR滤波器频率特性和期望频率特性之间的最大误差，利用Matlab信号处理工具箱中的Remez函数设计等纹波FIR滤波器［11，12］。

利用所设计的FIR滤波器对白噪声信号进行滤波，生成时域驱动信号。由于白噪声信号的功率谱均匀分布在整个频段内，因而大大减小了滤波生成的时域驱动信号的频谱泄漏现象。

2 自适应阻抗辨识

基于单步预测的Kalman滤波算法辨识振动实验系统的阻抗特性，利用自适应逆控制技术对系统的输入信号进行修正，使得系统的响应信号能够再现参考信号。

2.1 Kalman滤波器

Kalman滤波器基于随机状态空间模型给出了线性动态系统状态向量的最小均方估计。取状态向量的估计值为FIR滤波器的权值向量，图2给出了Kalman滤波器的实现框图［13］。

图2 Kalman自适应滤波器Fig.2 Kalman adaptive filters

图2中u(n)和y(n)分别为滤波器的输入和输出信号，d(n)为期望信号，e(n)为偏差信号，w^(n)为FIR滤波器权值向量的估计值。由图可知:

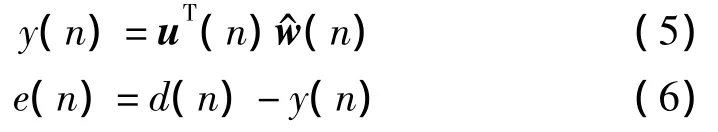
对于线性定常系统，Kalman滤波器的单步状态转移矩阵为常值。由于稳态时FIR滤波器的权值收敛于常数，或处于缓变状态，因此取单步状态转移矩阵为单位阵［14］。基于标准Kalman滤波算法可得

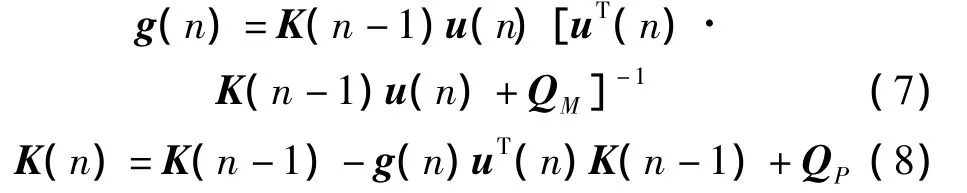
式中，g(n)为Kalman增益矩阵，K(n)为状态估计误差的相关矩阵，QM为测量噪声的相关矩阵，Qp为过程噪声的相关矩阵。基于e(n)和g(n)更新FIR滤波器权值向量的估计值:

式(5)～式(9)给出了基于单步预测Kalman滤波算法的FIR滤波器权值的最小均方估计递推公式。迭代过程趋于稳态时，FIR滤波器即为u(n)与d(n)之间脉冲传递函数的最优估计。

2.2 阻抗辨识

激振系统的输出信号往往存在噪声。由Kalman自适应滤波器原理可知，将系统输出信号作为滤波器的输入信号直接辨识系统阻抗时，无法得到阻抗特性的最优估计。而系统输出信号的噪声不影响自适应滤波器辨识传递函数的精度。因此，基于自适应逆控制原理，首先利用自适应滤波器辨识系统的传递函数，再通过辨识传递函数的逆得到系统的阻抗特性［15］。图3给出了基于Kalman自适应滤波器的阻抗辨识方法原理图。

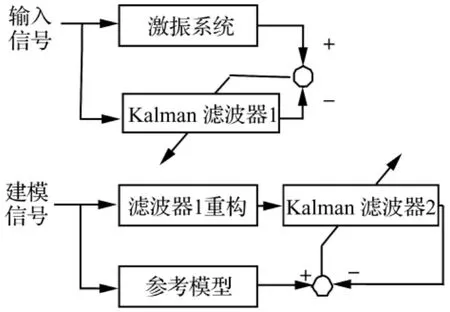
图3 基于自适应滤波器的阻抗辨识Fig.3 Inverse modeling based on adaptive filters

将激振系统的输入信号作为Kalman滤波器1的输入信号，系统的输出信号作为滤波器1的期望信号，基于单步预测Kalman滤波算法辨识激振系统的传递函数。

取限带白噪声信号作为建模信号，基于Kalman滤波器1的辨识结果，通过复制滤波器的权值重构滤波器1并对建模信号进行滤波，所得输出作为Kalman滤波器2的输入信号。将建模信号经参考模型之后的输出信号作为Kalman滤波器2的期望信号，基于单步预测Kalman滤波算法辨识Kalman滤波器1的阻抗特性。可知，滤波器2的辨识结果为参考模型和激振系统级联后的阻抗特性。

3 随机振动自适应控制算法

取延迟环节z－m(m为正整数)作为参考模型，图4给出了基于6自由度运动平台的随机振动自适应控制算法原理图。

图4中“运动学反解”和“运动学正解”模块用于在6自由度位姿信号和6路液压缸信号之间进行相互转换［16］。

利用参考谱的信息设计FIR滤波器，通过对白噪声信号滤波生成时域驱动信号。将时域驱动信号作为Kalman滤波器2的建模信号，通过复制Kalman滤波器2的权值重构滤波器2并对时域驱动信号进行滤波修正，所得输出作为6自由度运动平台的位姿输入信号。由2.2节分析可知，平台的位姿输出信号将再现延迟后的时域驱动信号。信号的延迟不改变其功率谱密度，因而使得6自由度运动平台的响应谱能够高精度再现参考谱信号。

图4 随机振动自适应控制算法Fig.4 Random vibration adaptive control

4 实验研究

为验证随机振动自适应控制算法的有效性，在图5所示6自由度运动平台Z方向上进行两组随机振动实验。

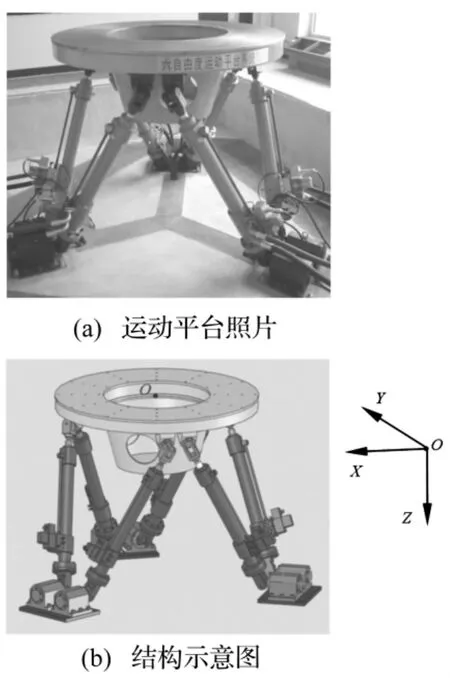
图5 6自由度运动平台Fig.5 6 Degree-of-freedom platform

参考谱由两段组成，在0.1 Hz～20 Hz为平直谱，20 Hz～25 Hz为下降谱，平直谱功率谱密度为7×10－9m2/Hz。取参考谱的±3 dB作为随机振动实验控制精度的容差限［17］，实验一中不修正时域驱动信号，将其直接作为6自由度平台的位姿输入信号，测量系统的响应信号。实验二中采用图4所示随机振动自适应控制算法控制平台运动。两组实验中均采用Welch方法估计响应信号的功率谱密度。

图6给出了参考谱和白噪声信号经FIR滤波器滤波后所得时域驱动信号功率谱的对比图。

由图6可知，经滤波生成的时域驱动信号的功率谱均在参考谱的±3 dB容差限内，表明基于滤波器设计理论的时域驱动信号生成方法是可行的。

图7给出了两组随机振动实验中的功率谱再现实验曲线。

图6 参考谱与时域驱动信号功率谱Fig.6 PSD of reference signal and time domain drive signal

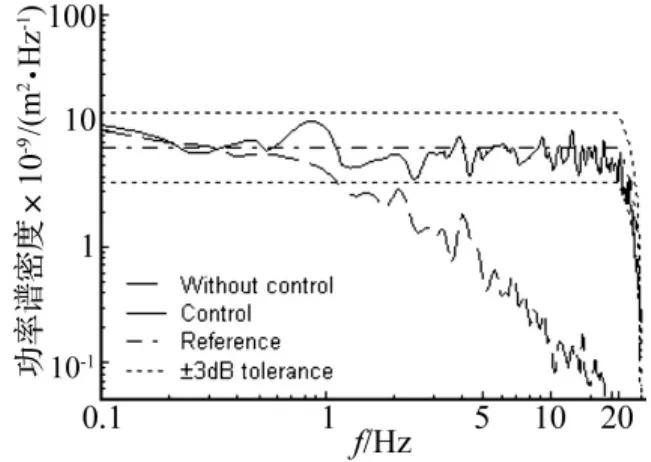
图7 随机振动实验结果Fig.7 Random vibration test results

由图7可知，无迭代补偿时系统的响应谱远远超出参考谱的±3 dB容差限，高频时(20 Hz附近)响应谱衰减甚至超过30 dB。采用随机振动自适应控制算法时，响应谱在整个频段内均控制在参考谱的±3 dB容差限内，实现了参考谱的高精度再现。

5 结论

提出了一种基于自适应滤波器的随机振动自适应控制算法。基于滤波器设计理论将参考谱转换为时域驱动信号，利用Kalman自适应滤波器实时在线辨识振动实验系统的阻抗特性，并对时域驱动信号进行滤波修正，通过再现时域驱动信号的方法再现参考谱信号。随机振动实验结果表明基于自适应滤波器的随机振动控制算法能够有效的拓展系统频宽，实现参考谱信号的实时高精度再现。

文中参考功率谱信号的频带为20 Hz。随着参考信号频带的提高，要求算法的运算周期随之减小。因此，进一步研究提高随机振动自适应控制算法收敛性及收敛速度的方法，将有利于高频参考谱信号的高精度再现。另一方面，设备或试件在实际工作环境中经受的振动是多维的，在多个轴向上同时存在。因此基于自适应滤波理论的多轴随机振动实时自适应控制算法也是后续的研究方向之一。

［1］Edwin A S.Vibration control system［P］.United States，4989158.1991－01－29.

［2］陈章位，于慧君.振动控制技术现状与进展［J］.振动与冲击，2009，28(3):73－77，86，200.

［3］韩 强，杜修力，刘晶波，等.多维地震作用下隔震桥梁地震反应(I)——模型结构振动台试验［J］.振动与冲击，2008，27(9):59－65，182－183.

［4］杨志东，丛大成，韩俊伟，等.基于扩展型准牛顿优化算法的单轴正弦扫频振动控制［J］.振动与冲击，2008，27(3):99－103，112，182－183.

［5］Stroud R C，Hamma G A.Multiexciter and multiaxis vibration exciter control systems［J］.Sound and Vibration，1988，22(4):18－28.

［6］Smallwood D O.Random vibration testing of a single test item with a multiple input control system［C］.Proceedings of the Institute of Environmental Sciences'28th Annual Technical Meeting，USA，Dallas，TX，1982:42－49.

［7］Stroud R C，Hamma G A，Underwood M A，et al.A review of multiaxis/multiexciter vibration technology［J］.Sound and Vibration，1996，30(4):20－27.

［8］Karshenas A M，Dunnigan M W，Williams B W.Adaptive inverse control algorithm for shock testing［J］.IEEE Proc-Control Theory and Applications.2000，147(3):267 －276.

［9］Groud D R，Gupta H O，Agarwal P.Design of random vibration controller using adaptive filtering［J］.International Journal of Recent Trends in Engineering，2009，2(5):75－79.

［10］Sayed A H，Kailath T.A state-space approach to adaptive RLS filtering［J］.IEEE Signal Processing Magazine.1994:18－60.

［11］The MathWorks，Inc.Filter design toolbox:designing advanced filters:optimal filter design solutions.Matlab Help Document［CP/CD］.US，MA:The Math Words，Inc，2002.

［12］McClellan J H，Parks T W.A personal history of the Parks-McClellan algorithm［J］.IEEE Signal Processing Magzine.2005，22(2):82－86.

［13］Haykin S.自适应滤波器原理［M］.第四版.郑宝玉等译.北京:电子工业出版社，2003，369－389.

［14］Qureshi S U H.Adaptive equalization［C］.Proceedings of the IEEE，1985，73(9):1349－1387.

［15］Widrow B，Walach E，Adaptive inverse control-a Signal processing approach［M］.Reissue ed.Hoboken，New Jersey:John Wiley＆ Sons，Inc.，2008，138－144.

［16］张尚盈，赵 慧，韩俊伟.六自由度运动平台实时控制的正/反解算法［J］.机床与液压，2003，(3):133－135，123.

［17］JB/T 8288－2001.中华人民共和国机械行业标准［S］.液压振动台.北京:中国机械工业联合会，2001.