高速列车振动荷载作用下电缆隧道结构动力响应分析

曲 村，高 亮，辛 涛，徐 亮

(1.北京交通大学 土木建筑工程学院，北京 100044;2.北京市市政工程设计研究总院，北京 100045)

城市中地下管线铺设较为复杂，在修建城市轨道或者城际高速铁路时，会出现铁路线修建在地下管线上方的情况。由于城际高速铁路列车运行速度较快，高速车辆振动荷载可能会对铺设地下管线的隧道结构产生不利的动力影响，需要对此进行动力学方面的研究。

本文以京津城际轨道交通工程为例进行研究。在北京市南二环路玉蜓桥东侧上，京津城际跨越了北京电力公司的一条2.0 m×2.0 m电缆隧道。由于京津城际无法避让，无法对电缆隧道进行迁改，采用了桩板结构跨越该电缆隧道，本文主要针对该措施进行研究。

1 研究思路

为了研究高速车辆对铺设地下管线的隧道结构产生的动力影响，本文首先运用耦合动力学思想，建立车辆－轨道耦合系统振动分析模型。利用较成熟的FORTRAN语言编写的动力学仿真计算程序，研究列车以一定速度从电缆隧道上方通过时桩板结构的受力情况，为研究列车荷载对下部结构的影响提供动力荷载谱。

然后，利用有限元理论建立桩板－土体－隧道一体化动力仿真模型。将车辆－轨道耦合系统振动分析模型得到的荷载谱作为外部激励作用在桩板－土体－隧道一体化动力仿真模型上，对电缆隧道的动力响应进行研究。

最后，根据车辆－轨道耦合系统振动分析模型和桩板－土体－隧道一体化动力仿真模型相结合得到的计算结果，研究京津城际运营后列车振动荷载对电缆隧道结构的影响。根据疲劳寿命、强度、变形和加速度等方面的评价标准，给出列车振动荷载对电缆隧道影响的评估结论。

2 计算模型及参数

2.1 车辆－轨道耦合系统振动分析模型

本文采用车辆－轨道耦合动力学的思想和理论［1－4］，建立了具有二系悬挂的整车模型、连续分布参数的轨道结构模型、轮轨耦合模型以及轨道不平顺模型。

根据车辆的结构形式、悬挂特性，将车体、转向架、轮对视为刚体，车辆模型就变成由车体、转向架、轮对组成的多刚体系统，彼此之间通过弹簧阻尼器元件连接。在车辆－轨道耦合系统振动分析模型中，车体和转向架各有3个自由度，即沉浮、点头、侧滚;每个轮对具有2个自由度，即沉浮、侧滚。

轨道由钢轨、扣件系统、轨道板、砂浆调整层以及水硬性支承层组成，钢轨由扣件等间距定位在轨道板上，混凝土基础考虑为刚性基础。在模型中只考虑钢轨的弯曲变形，而不考虑其剪切变形，钢轨单元看作点支撑等截面梁。轨道板在模型中采用弹性薄板单元进行处理。

车辆－轨道耦合系统振动分析模型如图1所示。

图1 车辆－轨道耦合系统振动分析模型Fig.1 Vibration analysis model of vehicle-track coupling system

车辆方面，采用国产300km/h动力分散式列车组参数。车辆全长26.3 m，定距18 m，轴距2.5 m，轴重14.5 t，车体质量 42.4 t，构架质量 3.4 t，轮对质量2.2 t。

轮轨之间的耦合作用，通过轮轨接触来实现。根据Hertz非线性弹性接触理论计算轮轨垂向力。

轨道方面，采用60 kg/m钢轨;扣件刚度为50 kN/mm;轨道板长6.45 m，宽2.55 m，厚0.2 m，相邻板缝为50 mm;砂浆调整层厚度30 mm;水硬性支承层厚0.3 m，宽3.25 m。轨道断面图如图2所示。

图2 轨道断面图Fig.2 View of track section

对于轨道不平顺，分别选取确定性不平顺和随机不平顺作为系统的激励。

按照文献［5］规定，无砟轨道的平顺度铺设精度，高低不平顺小于2 mm/10 m。又根据高速铁路正线轨道动态几何尺寸容许偏差及列车振动管理值［6］，对于高低不平顺，舒适度管理值为8 mm(小于40 m波长)和11 mm(小于80 m波长)，紧急补修管理值为10 mm。对于确定性不平顺，本文保守地取波幅10 mm，波长10 m的轨道不平顺作为系统的激励。

由于缺乏京津城际铁路采用的随机不平顺，本文选取德国低干扰轨道谱作为系统的激励。德国低干扰轨道谱可以用于时速250km以上的高速铁路。

2.2 桩板－土体－隧道一体化动力仿真模型

京津城际轨道交通工程在跨越电缆隧道时，采用了跨度16 m的桩板结构，墩台基础采用直径80 cm钻孔管灌注桩。桩板结构的竖向布置如图3所示。

支点及梗肋部梁高1.5 m，跨中梁高1.0 m。采用C40钢筋混凝土，弹性模量3.4 ×104MPa，容重25 kN/m3，混凝土泊松比0.2。桩板结构横向宽为12.4 m，斜交布置，斜角角度83.61°。桩板结构的横向布置如图4所示。

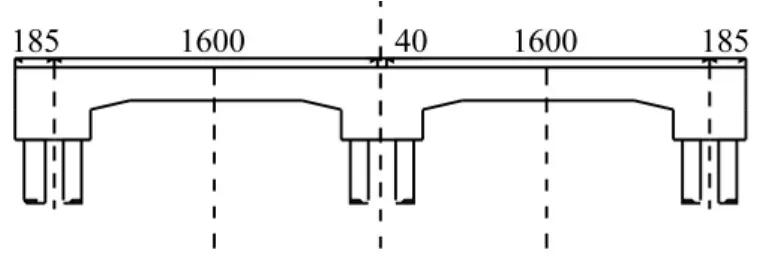
图3 桩板结构竖向布置Fig.3 Vertical disposal of pile-slab structure

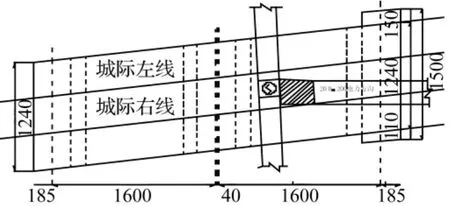
图4 桩板结构横向布置Fig.4 Transverse disposal of pile-slab structure

每个墩台桩基础均采用12根直径0.8 m钻孔桩，中墩设计桩长为26m，边墩设计桩长为24 m。采用C30钢筋混凝土，弹性模量 3.2×104MPa，容重 25 kN/m3，混凝土泊松比 0.2。

既有电缆隧道防护结构为钢筋混凝土框架箱涵，管道内尺寸2.0 m ×2.0 m，顶、底板厚度 0.4 m，边墙厚度0.3 m。电缆隧道采用C40钢筋混凝土，弹性模量3.4 ×104MPa，容重 25 kN/m3，混凝土泊松比0.2。

列车高速通过电缆隧道区域时，列车和轨道之间的动作用力经钢轨、扣件系统、轨道板、板下砂浆垫层和水硬性支承层等结构传至桩板结构顶端。通过建立桩板－土体－隧道一体化动力仿真模型，研究列车引起的动载经桩板结构、土层传至电缆隧道时电缆隧道结构的动力响应。

桩板结构有限元模型如图5所示。隧道结构有限元模型如图6所示。桩板结构与隧道结构斜交模型如图7所示。

图5 桩板结构有限元模型Fig.5 Finite element model of pile-slab structure

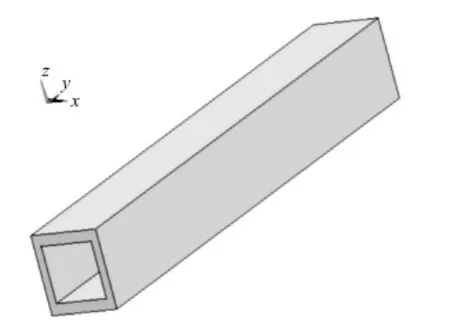
图6 隧道结构有限元模型Fig.6 Finite element model of tunnel structure

将桩板结构、隧道结构和土体有限元模型结合在一起，形成相互耦合的桩板－土体－隧道一体化动力仿真模型如图8所示。

在采用有限元法模拟半无限介质的波动问题时，在截断边界处会引起应力波的反射，使计算失真，故如何设置人工边界消除假反射是有限元法求解波动问题的关键。本文在考虑了计算的精度和运算的时间后，在有限元模型的边界处采用了弹簧阻尼边界(粘弹性边界)［7］，如图 9 所示。

图7 桩板结构与隧道结构斜交模型Fig.7 Oblique crossing model of pile-slab structure and tunnel structure

图8 桩板－土体－隧道一体化动力仿真模型Fig.8 Pile-slab-soil-tunnel longitudinaltransverse-vertical spatial coupled dynamic simulation model

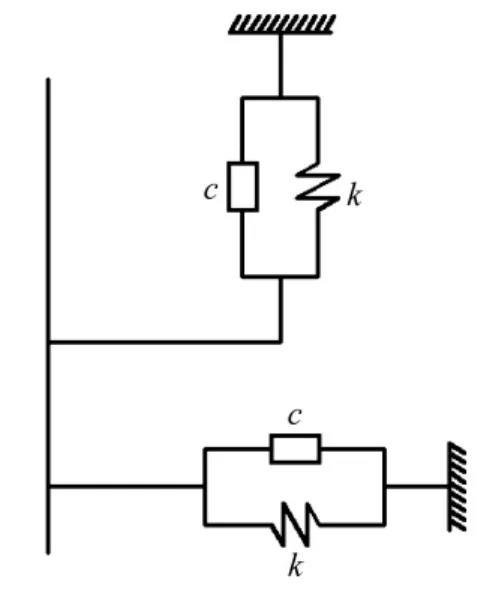
图9 弹簧阻尼边界Fig.9 Boundary of spring-damping

2.3 计算工况

本文采用确定性不平顺和德国低干扰谱两种激励，分别考虑左线单线行车、右线单线行车、双线同向行车和双线对向行车四种工况。结合上述车辆－轨道耦合系统振动分析模型和桩板－土体－隧道一体化动力仿真模型，得出计算结果。

3 列车荷载作用下隧道的动力响应

3.1 确定性不平顺激励下的动力响应

以采用确定性不平顺激励、桩板结构上左线单线行驶车辆为例，给出动力作用下的隧道变形结果如图10所示，隧道应力结果如图11所示，隧道加速度结果如图12所示。

采用确定性不平顺激励时，考虑四种计算工况，桩板结构下电缆隧道的动力响应计算结果汇总如下:

电缆隧道的纵向变形最大值为0.03 mm，横向变形最大值为0.05 mm，垂向变形最大值为0.94 mm，双线同向行车时变形最大;电缆隧道的纵向动应力最大值为23.70 kPa，横向动应力最大值为 4.60 kPa，垂向动应力最大值为6.39 kPa，双线同向行车时动应力最大;电缆隧道的纵向加速度最大值为2.64 cm/s2，横向加速度最大值为7.28 cm/s2，垂向加速度最大值为9.93 cm/s2，双线同向行车时加速度最大。

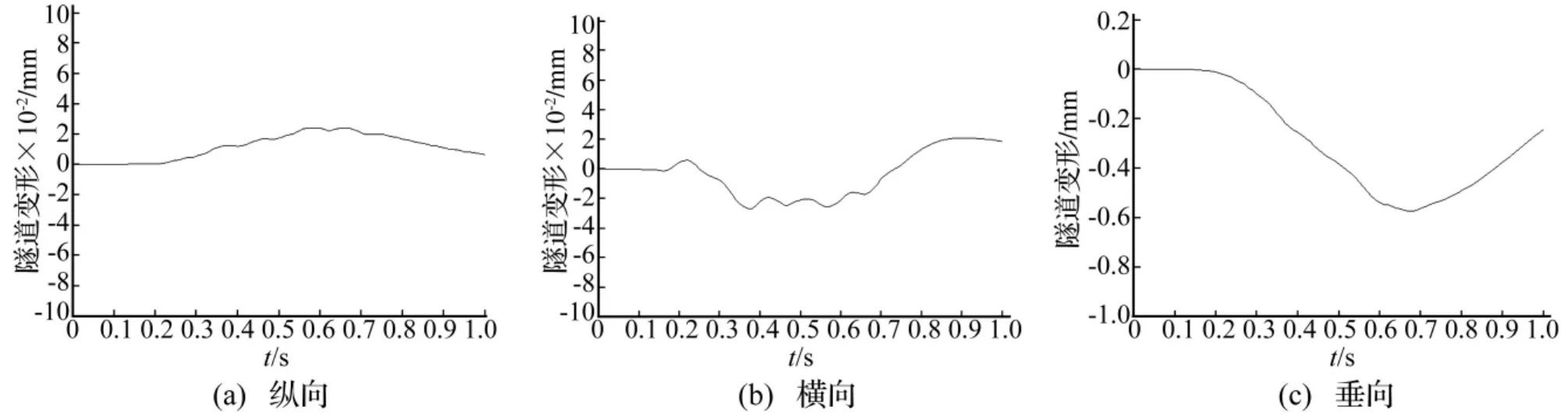
图10 隧道变形时程曲线图Fig.10 Time interval graph of tunnel deformation

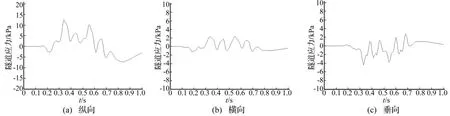
图11 隧道应力时程曲线图Fig.11 Time interval graph of tunnel stress

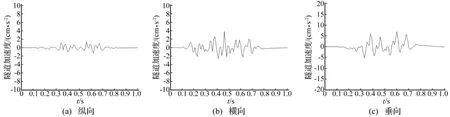
图12 隧道加速度时程曲线图Fig.12 Time interval graph of tunnel acceleration

由以上采用确定性不平顺激励时的动力响应计算结果可知，双线同向行车时隧道结构的变形、动应力以及加速度皆最大。

3.2 德国低干扰谱激励下的动力响应

采用德国低干扰谱激励，考虑四种计算工况，桩板结构下电缆隧道的动力响应计算结果汇总如下:

电缆隧道的纵向变形最大值为0.01 mm，横向变形最大值为0.05 mm，垂向变形最大值为0.92mm，双线同向行车时变形最大;电缆隧道的纵向动应力最大值为22.81 kPa，横向动应力最大值为 4.94 kPa，垂向动应力最大值为6.87 kPa，双线同向行车时动应力最大;电缆隧道的纵向加速度最大值为3.59cm/s2，横向加速度最大值为9.94 cm/s2，垂向加速度最大值为9.98 cm/s2，双线同向行车时加速度最大。

由以上采用德国低干扰谱激励时的动力响应计算结果可知，双线同向行车时隧道结构的变形、动应力以及加速度皆最大。

3.3 结果汇总

桩板结构下电缆隧道动力响应的最大值见表1和表2。

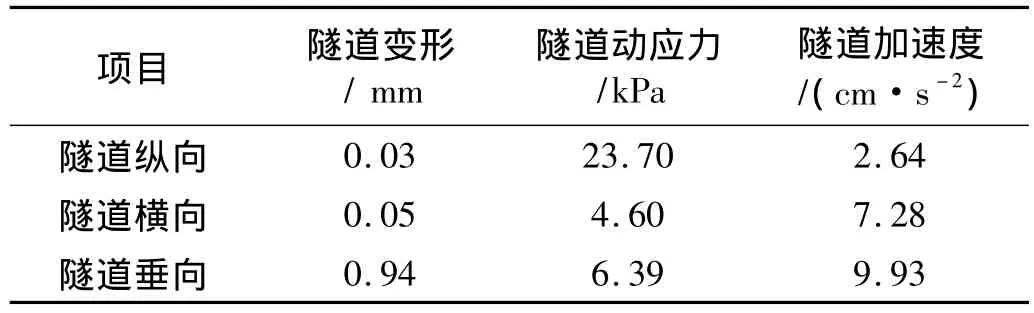
表1 确定性不平顺激励下动力响应的最大值Tab.1 Maximum of dynamic response under deterministic track irregularity stimulus

表2 德国低干扰谱激励下动力响应的最大值Tab.2 Maximum of dynamic response under Germanic interferential spectrum stimulus

综上所述，动力荷载作用下，桩板结构下的电缆隧道的最大变形为0.94 mm，最大动应力为23.70 kPa，最大加速度为9.98 cm/s2。

4 电缆隧道动力响应评估

4.1 电缆隧道疲劳寿命评估

列车荷载的长期反复作用，可能会造成电缆隧道的疲劳问题，下面就列车荷载反复作用对电缆隧道疲劳寿命的影响进行了分析。

根据Aas-Jakobsen公式［8］，混凝土材料的疲劳寿命根据下式得出:

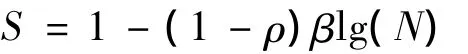
式中，S为应力水平，定义为作用在试件上的最大荷载与构件静载使用荷载之比;

ρ是荷载循环特征值，即循环荷载的最小值与最大值之比，一般取0.1 或0.2;

β为试验参数，对于某一特定混凝土材料β为定值，Aas-Jakobsen建议 β=0.0640;

N为混凝土的疲劳寿命，即在应力比S作用下混凝土所能承受的最大疲劳次数。

根据建模计算的结果，并取最不利的最大荷载与构件静载使用荷载之比，代入上面的Aas-Jakobsen公式计算得疲劳寿命约为1012次。按照城际铁路列车每10分钟一趟，每天运营24个小时(实际上会小于这个数字)，则一年可通过的列车次数为52560次，假使按照轨道的设计年限为一百年来计算，其通过次数为5256000次，约500多万次，远小于计算得到的混凝土材料的疲劳寿命1012次。从混凝土材料疲劳寿命的角度进行分析，电缆隧道结构的疲劳寿命能满足要求。

4.2 电缆隧道强度评估

根据文献［9］，C40混凝土的最小强度设计值为1710 kPa，远大于桩板结构下电缆隧道的最大应力23.70 kPa，电缆隧道结构强度能满足要求。

4.3 电缆隧道变形评估

根据计算结果，桩板结构下电缆隧道的最大变形为0.94 mm，能够满足实际工程的要求。

4.4 电缆隧道加速度评估

根据计算结果，桩板结构下电缆隧道的最大加速度为9.98 cm/s2，能够满足实际工程的要求。

5 结论与建议

本文对桩板结构条件下高速列车振动荷载对电缆隧道结构的影响进行了评估。由采用确定性不平顺激励和德国低干扰谱激励时的动力响应计算结果可知，在左线单线行车、右线单线行车、双线同向行车和双线对向行车四种工况中，双线同向行车时隧道结构的变形、动应力以及加速度皆最大。

根据本文所采用的参数和计算结果，在疲劳寿命、强度、变形和加速度等方面，本文所述高速列车振动荷载的动力作用不会对桩板结构下的电缆隧道产生显著的不利影响。本文偏重于理论研究，将来如有条件，应结合具体工程进行测试，对计算结果进行验证，以便更好地指导工程设计。

［1］夏 禾.车辆与结构动力相互作用［M］.北京:科学出版社，2002.

［2］翟婉明.车辆－轨道耦合动力学.第三版［M］.北京:科学出版社，2007.

［3］Xin T，Gao L，Qu J J.Research on Vibration Characteristics of Floating Slab Track in Rail Transportation System［C］//The Third International Symposium on Environment Vibrations:Prediction， Monitoring， Mitigation and Evaluation(ISEV2007)，Taipei，2007.

［4］Liao L，Gao L，Hao J F.Study on the Dynamics Vibration Character of the Concrete Slab Track in Track Traffic System of Linear Induction Motor［C］//The Third International Symposium on Environment Vibrations:Prediction，Monitoring，Mitigation and Evaluation(ISEV2007)，Taipei，2007.

［5］中华人民共和国铁道部.铁建设［2007］47号，新建时速300～350公里客运专线铁路设计暂行规定［S］.北京:中国铁道出版社，2007.

［6］卢祖文.客运专线无碴轨道［M］.北京:中国铁道出版社，2005.

［7］翟 辉.北京地铁四号线北大段综合减振措施理论模拟研究［D］.北京:北京交通大学，2006.

［8］庞林飞.钢筋混凝土板疲劳损伤识别及疲劳寿命预测［D］.南京:东南大学，2004.

［9］中华人民共和国建设部.GB50010－2002，混凝土结构设计规范［S］.北京:中国建筑工业出版社，2002.