微弱信号强干扰分离方法研究

李秀坤，李婷婷，马 涛

(哈尔滨工程大学 水声技术实验室，哈尔滨 150001)

水声传播理论发展的近百年过程中，主要关注的是声波在海水介质中的传播。根据浅海波导声传播的理论，简正波在波导中传播的频率低于截止频率时不能在水中传播［1］。尤其在夏季浅海中普遍存在负梯度水文现象，水中传播的声波将会急剧地折射向海底，此时水中的声波更易于通过海底传播，而不是通过水中传播。近几十年来人们对海底地质声学特性的认识不断深入，推动了对低频和极低频声传播研究的不断发展［2－4］。基于陆地的探测手段可以不受海洋水文环境的限制，全天候的对潮汐引起的地壳运动、海洋环境参数进行测量、探测水中目标。

理想情况下，测量系统需要一个绝热、隔振的环境，以避免环境因素如:振动、温度、湿度、气压等对测量的影响。但在实际的测量环境中，接收系统很难达到绝热真空处理，并且对空气扰动和低频振动极其敏感，这些随机干扰将直接影响接收系统的接收效果，所以在接收信号中会存在随机的强低频干扰，这类干扰称为趋势项干扰。

趋势项的存在，会使时域中的相关分析和频率中的功率谱产生大的误差，甚至使低频谱完全失去真实性［5］。现有的趋势项消除方法有几种［6－8］，如平均斜率法、差分法、低通滤波法及最小二乘拟合方法等。这些方法通常需要预先假定信号中趋势项的类型，如线性趋势或指数趋势等等，不适用于具有复杂变化趋势或随即变化趋势的信号，因此不具有普遍的适用性。经验模态分解(EMD)方法是一种全新的处理方法，该方法依据信号本身固有的特征自然的分解信号，无需设置先验的分解基函数，因而适用于处理各种不同类型的数据。

1 经验模态分解方法

希尔伯特－黄变换(HHT:Hilbert-Huang Transform)是美国工程院院士Huang及其合作者［9］在20世纪末提出的一种新的非线性、非平稳时间序列分析方法。它基于经验模态分解，将信号分解为一系列固有模态函数(IMF:Intrinsic Mode Function)之和，对每一个固有模态函数进行Hilbert变换，得到其瞬时频率，并将其以时间—频率为坐标的平面表示出来，得到时间－频率－能量的分布，称为Hilbert谱。从理论上分析，HHT不仅解决了多辐射声源时小波分析的分辨率问题和对不同声源信号的适应性问题，而且解决了Winger-Ville分布的多分量信号交叉项问题。本文采用EMD方法将实测信号分解成一系列IMF，其结果是将信号中不同尺度的波动或趋势逐级分解，产生一系列具有不同特征尺度的数据序列，达到分离趋势项的目的。

1.1 经验模态分解

EMD分解方法基于以下几点假设:(1)信号至少有两个极值点，一个极大值和一个极小值，或者极大值或极小值数目比零点的数目多2个(或2个以上);(2)信号的特征时间尺度是由极值点之间的时间间隔确定的;(3)如果数据中缺乏极值点，但存在奇异点，可以通过一次或多次差分来求出极值点。

EMD分解的具体处理方法是，找到数据x(t)的极大值点集和极小值点集后，用插值法拟合x(t)的上、下两条包络线。计算两条包络线的平均值，记为m1(t)。计算得到x(t)与m1(t)的差，记为h1(t)，即:

一般来讲，h1(t)仍然不是一个IMF分量，为此需要对它重复上述处理过程。即将h1(t)视为新的数据序列，拟合其上、下包络，得到两条包络线的平均值m11(t)，并计算h1(t)与m11(t)的差值，记为h11(t)，即:

重复以上操作i次，直到h1i(t)满足IMF的条件为止，至此得到了信号x(t)的第一个IMF分量，记为:

从数据中分离出imf1，即:

若剩余量r1(t)仍含有较长的周期成分，则将其看作新的数据，并重复以上步骤，分解出新的IMF:

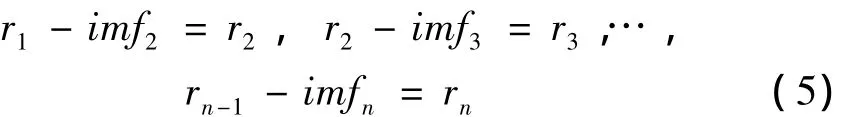
当剩余量变为一个常量，或者一个单调函数，再或者一个有且仅有一个极点的函数时，数据筛分结束。此时的rn(t)称为余项，每一个筛分出的IMF分量与前一个筛分出的IMF分量相比，含有较低的频率特性。最后，原始的数据序列即可由这些IMF分量以及一个均值或趋势项表示:

1.2 EMD方法的终止条件

文中采用简单收敛准则，即只要信号的极值点和过零点的数目相等时，筛选过程就终止准则。这种停止准则很简单，同时考虑了IMF的定义，更加趋于合理化。通过仿真研究，在实际中很难达到信号的极值点和过零点的数目相等。因此，本文在使用此准则时，将终止条件设置为信号的极值点与过零点的数目相等或至多相差1，即可停止筛选。并设置最多循环1200次如不满足简单收敛准则，则强制退出。

1.3 趋势项的确定

缓慢趋势项的估计可能是分解后的余项和几个低频模式分量的和，即认为从第D个基本模式分量到最后一个基本模式分量和余项的和。由此可以得到信号的缓慢趋势项为:

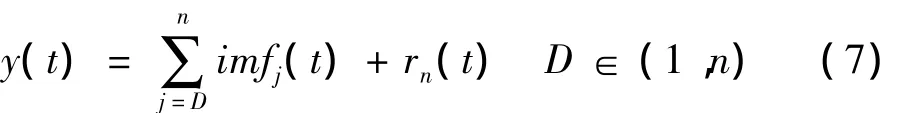
其中，n和rn(t)分别是经EMD分解得到的基本模式分量的个数和余项。

为了确定D值的大小，首先定义前d个基本模式分量的和为:

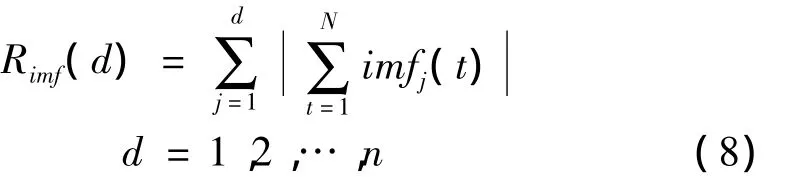
根据EMD分解原理可知，每个模式分量的均值都应该为零。但是由于一个IMF可能包含非整数个周期，所以在实际应用中Rimf(d)可能是非零的。并且随着分解阶数i的增大，IMF的周期也将增大，随之由于非整数周期引起的前i个IMF分量绝对值的和也单调增加。因此，可以观察Rimf(d)随分解阶数i的变化情况，在d≥D后明显地偏离零点便可以认为此时的IMF进入了缓慢变化的状态。取使Rimf(d)明显偏离零点时的d值作为D，然后用式(7)进行重构，就可以获得所求的缓变趋势项。

2 实测信号的数据处理

测量系统在进行接收信号，地声测量系统采集的数据的时域和频域如图1。观察实测数据的时域和频域上的特性不难看出，数据中存在极强的趋势项干扰，并且趋势项的形式非常复杂，而感兴趣的信号部分则相对较弱。为了实现强干扰的抑制和提高弱信号的检测与识别能力，便需要进行强干扰的分离与去除。

图1 实测信号的时域波形和功率谱Fig.1 Time-domain waveforms and power spectrum of achual signal

图2为采用最小二乘法拟合指数型的趋势项所构造得到的对于趋势项的近似估计和去除趋势项后信号的时域结果。采用最小二乘法只能近似拟合数据中趋势项，对于复杂形式的趋势项不能够很好的拟合出来。并且，这种趋势项的构造方法并不是按照信号组成成分的意义进行构造的，容易破坏有用信号成分或是没有完全去除趋势项部分。因此，利用这种方法去除趋势项具有很大的局限性。

现采用EMD方法将实测信号分解成一系列的IMF，其结果是将信号中不同尺度的波动或趋势逐级分解，产生一系列具有不同特征尺度的数据序列，从而达到分离强干扰的目的。对实测数据经过EMD分解得到的12个IMF分量和一个余项，如图3。Rimf(d)随分解阶数i的变化情况如图4所示。

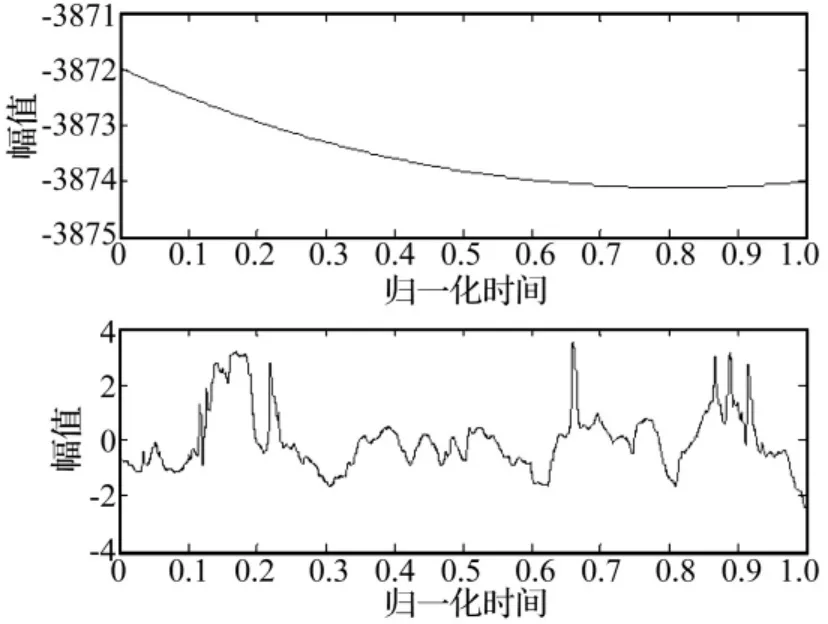
图2 最小二乘法去趋势项Fig.2 Tendency removing by least square method

按照文中所指出的趋势项判断方法分析，当d≥4时，Rimf(d)的值明显地偏离了零点。因此取D=4，即利用第5到第12个基本模式分量和余项根据式(7)重构就可以得到信号的缓变趋势项。处理结果如图5所示，其中上图为消除趋势项后的信号的时域图，图5为所去除趋势项的时域图。

图3 EMD分解的IMF分量和余项Fig.3 IMF and residue of the EMD

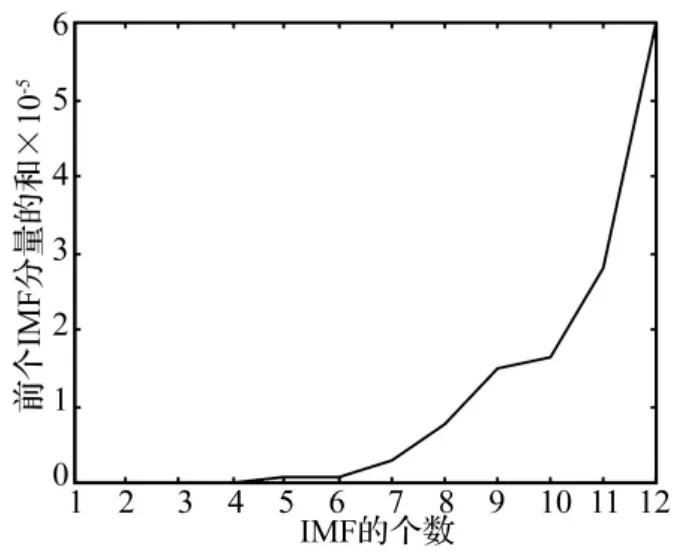
图4 前i个IMF分量的和Fig.4 Summation of the first i IMFs

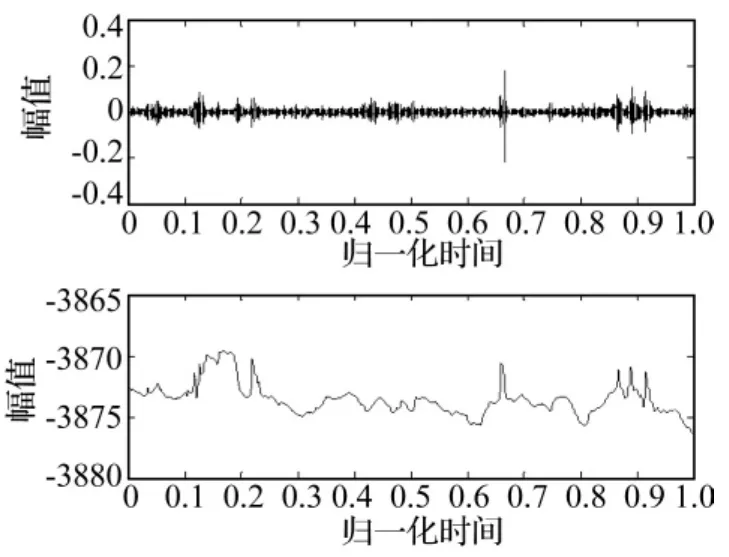
图5 期望信号和所剔除的趋势项的时域图Fig.5 Time-domain waveforms of the expect signal and the tendency

处理结果表明，利用EMD分解可以有效的提取出实测信号中的趋势项。与基于最小二乘的趋势项拟合方法相比，这种方法能有效地提取并分离出复杂的趋势项成分。

3 结论

实测信号是多源混合信号，存在形式复杂的强趋势项干扰，而真正所感兴趣的信号部分则相对较弱。EMD算法简单，无需任何的先验知识就可以自适应的把一个多分量信号进行分解，并且不损失信号成分。针对实测信号的特点，文中给出了根据IMF分量进行趋势项判别与重构的方法。实际数据的处理结果表明，文中方法可以有效地提取出复杂的趋势项。

［1］何祚镛，赵玉芳.声学理论基础［M］.北京:国防工业出版社，1981.

［2］Chapman N R，Chin-Bing S，King D，et al.Special issue on geoacoustic inversion in range-dependent shallow-water environments［J］.IEEE J.Oceanic Eng，2003，28(4):317－319.

［3］Chapman N R，Chin-Bing S，King D，et al.Inversion techniques workshop:Range dependent test cases［J］.IEEE J.Oceanic Eng，2003，28:320 －330.

［4］Fulford J K，King D，Chin-Bing S，et al.Benchmarking geoacoustic inversion methods using range-dependent field data［J］.IEEE J.Oceanic Eng，2004，29:3 －12.

［5］高品贤.趋势项对时域参数识别的影响及消除［J］.震动、测试与诊断.1996，14(2):20 －26.

［6］Bendat JS， PiersolA G. Random dataanalysisand measurement procedures［J］.Second Edition.John Wiley ＆Sons，1986，12:396 －398.

［7］王广斌，刘义伦，金晓宏，等.基于最小二乘原理的趋势项处理及其 MATLAB的实现［J］.有色设备，2005，1003－8884，05 －04 －05.

［8］王宏禹.非平稳随即信号分析与处理［J］.北京:国防工业出版社，1999.

［9］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proc.Roy.Soc.London A，1998，454:903 －995.