坡膛结构变化对弹带挤进过程影响的研究
孙河洋,马吉胜,李 伟,刘海平,齐 琦
(1.军械工程学院,石家庄 050003;2.66362部队 装备部,北京 101200)
弹丸及弹带冲击坡膛的研究需详细了解弹带挤进膛线的机理。弹带挤进过程即弹带随弹丸运动并挤入膛线的过程,其是一个极其复杂的非线性力学过程,分别涉及非线性问题的三大方面:材料非线性,即弹带材料的大变形、大应变及损伤失效问题;几何非线性,即弹丸、弹带在运动过程中的大位移及旋转问题;边界条件非线性,即弹带材料与坡膛的接触问题。由于其涉及到弹带在快速变化的压力作用下的高度非线性问题,且经历的时间及行程非常短,用实验测量比较困难。内弹道中常用静压法和截短枪管射击法来测量挤进压力,为此经典内弹道学模型进行了简化,假设膛内压力达到了挤进压力时弹丸瞬时挤进。目前,国内外对此方面的研究报道尚不多见。文献[1]通过研究弹丸滑移线建立平衡方程来近似计算接触应力,但滑移线是通过实验的观察粗略估计所得,且忽略了坡膛角,具有较大的局限性。文献[2]运用微元分析法建立平衡方程,计算得到自润滑弹带挤进时期的接触应力。文献[3]通过适当简化建立弹带挤进模型,进行了弹带挤进坡膛的受力分析及弹丸在静载平衡条件下的弹丸运动阻力,并以动载系数进行修正。文献[4]考虑了高速冲击下弹带材料的应变特性并建立相关模型模拟挤进。文献[5,6]通过构建简化模型分别计算了双头弹的挤进阻力。相关文献进行了静态及准静态的实验研究。以上文献在合理简化的基础上,采用微元分析的方法建立二维的弹带挤进模型,对经典内弹道学进行了有益的补充。本文在此基础上进一步完善对弹带材料高度非线性行为的描述,建立弹带材料的初始损伤及累计损伤失效模型,运用显式非线性有限元算法对两种不同结构坡膛的挤进过程进行瞬态动力学的数值模拟,研究了坡膛结构变化对弹带挤进冲击身管内壁的影响,从而为从力学角度揭示某型火炮坡膛裂纹形成机理奠定了理论基础。
1 计算模型
1.1 有限元模型
本文以某型火炮及其改进型的坡膛及弹丸、弹带为研究对象,运用有限元前处理软件建立8节点六面体有限元实体单元模型,如图1、图2所示。
1.2 计算工况模型
本文分析了弹带挤进某型火炮坡膛及其改进型坡膛两种挤进工况下弹丸、弹带对坡膛的冲击影响,两工况下坡膛长度分别取为40 mm及100 mm,弹带及弹丸的尺寸均保持不变。弹底压力分别来自两火炮计算说明书所提供的数据。

图1 弹丸及坡膛有限元模型Fig.1 Finite element model of bore and projectile

图2 弹带局部放大有限元模型Fig.2 Finite element model of band
2 材料模型
坡膛和弹丸均采用普通炮刚的材料模型。弹带材料为某型铜,由于弹带在挤进过程中涉及到大变形、大应变以及材料失效等高度材料非线性问题,故采用Johnson-Cook屈服模型及累计损伤失效模型。
2.1 弹带的屈服模型
弹带材料采用Johnson-Cook屈服模型,该模型中屈服应力是塑性应变、应变率以及温度的函数:

其中,εp为等效塑性应变;为等效应变率;ε0为参考应变率;T为温度;Tr为室温;Tm为融化温度;A、B、C、m和n是常量。
2.2 弹带材料的损伤失效模型[7,8]
各向同性硬化弹塑性材料的损伤可表现为两种形式:即屈服应力的软化和材料刚度的退化。如图3所示,实线代表含损伤材料的应力应变曲线,虚线代表无损材料的应力应变曲线。图3中σy0和分别为初始损伤的屈服应力和等效塑性应变为失效时的等效塑性应变。

当总体损伤变量D=0时,材料无损伤;当材料的总体损伤变量D不为零时,损伤材料的刚度退化为E(1-D);当总体损伤变量D=1时,材料的刚度退化为零,材料发生失效。由图3所示,若在A点进行卸载,应力应变曲线沿直线AB下降至B点处,B点处的值即为损伤材料卸载后的等效塑性应变值。
2.2.1 弹带材料的初始损伤模型
延性金属的断裂可归结为晶粒的成核、生长、空穴的合并和剪切带的形成等两方面因素的影响,基于以上现象,延性金属的初始损伤可分为断裂延性金属损伤和颈缩延性金属损伤两类,本文选用Johnson-Cook初始损伤准则,该准则以等效塑性应变来界定初始损伤:

其中,d1-d5为失效参数,ε0为参考应变率,为无量纲温度,其表达式如下:
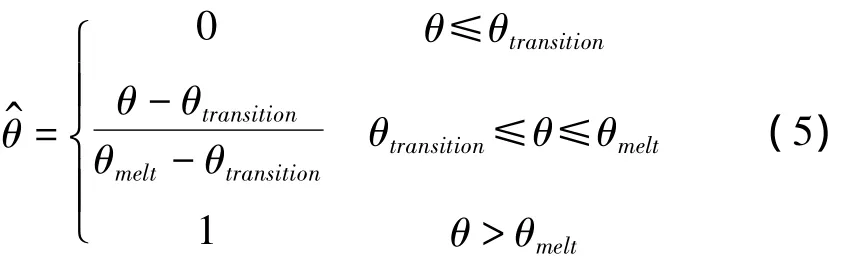
其中,θ为当前温度,θmelt为融化温度,θtransition为转换温度,当材料当前温度低于转换温度时,材料的损伤与温度无关。

图3 材料损伤模型示意图Fig.3 Sketch map of the damage model
2.2.2 基于能量的损伤演化模型
材料损伤的出现加大了数值计算对细密网格的依赖性,文献[7]引入了断裂能量方法以减少网格依赖性:即初始损伤后将应力应变关系转化为应力位移关系,并引入裂纹的单位面积断裂能Gf为材料参数。

其中L为与单元积分点及尺寸有关的单元特征长度,u-pl为等效塑性位移,且:

定义损伤变量:

如式(6)所示,断裂能Gf为屈服应力在等效塑性位移上的积分,其随等效塑性位移的增加而趋近于零,故由式(8)使材料损伤过程中的能量耗散等于断裂能Gf,当损伤变量d趋近于1时,材料发生失效。
3 接触模型及显式算法实现
弹带挤进过程的有限元模型中共存在三个接触对:弹带与坡膛内壁、弹带与弹丸及弹丸与身管内壁,其中弹丸与身管皆设置为弹性接触。本文采用罚函数法进行接触建模,其可由广义变分原理引入罚函数来实现。构造如下泛函:

其中,U为应变能,W为外力功,G为约束条件所对应的约束项。
对式泛函π取变分:
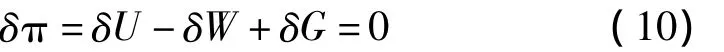
其中,


式(10)可离散为如下运动微分方程的形式:
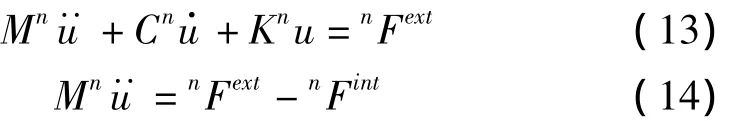
式中nFext为外载荷矢量,为内力矢量,n为当前时间步。
对质量阵求逆可得:

将单元质量分布在节点上使M成为集中质量矩阵,即M为对角阵,则:

假设速度在一个时间步长内是恒定值,在时间推进上采用中心差分法:

4 数值模拟及结果分析
本文对所建立的两种工况下的挤进模型进行了数值模拟,两种工况下弹带分别于2.8 ms及3.2 ms左右完全挤进全深膛线。图4为弹带完全挤进后的变形图,从图中可以看出弹带材料在挤进过程中产生了塑性大变形,且被阳线挤压导致材料失效形成凹槽状挤痕,与实弹射击后回收弹带的变形情况一致。
火炮击发点火后,火药气体压力迅速上升迫使弹带挤进膛线,从而产生塑性变形阻力,其与摩擦阻力合成弹带挤进膛线阶段的弹丸运动阻力。随着挤进行程的增加,弹带变形量增加,变形阻力增大,当弹带完全挤进全深膛线时,变形阻力达到极大值,故本文两种工况均选取阳线起点处相同位置的一个单元及节点进行受力分析,如图5所示。工况1的弹带长度大于坡膛长度,其实质是弹带轴向塑性变形量增加,因而相对工况2,其弹带的变形阻力及弹丸的启动压力P0相应增加。弹带变形阻力的增加导致弹带对坡膛正压力的增加即挤进摩擦阻力相应增加。故工况1弹带的变形阻力和挤进摩擦阻力均大于工况2的相应阻力,如图6所示的挤进加速度对比曲线,由于挤进阻力较大,在完全挤进前工况1的加速度始终小于工况2。

图4 弹带挤进变形图Fig.4 Deformation of band after pulling in

图5 坡膛局部有限元模型Fig.5 Parts of FE model of bore
图7所示为两工况下挤进速度的对比曲线,可知工况1的挤进速度始终小于工况2。由内弹道理论可知:从弹带挤进膛线开始一直到出膛口为止的过程为内弹道循环的主要过程,此过程与火药的燃烧、弹丸的运动、弹带的挤进及其与膛壁的摩擦关系密切。一方面火药的燃烧使弹后气体不断膨胀,压力上升;另一方面弹丸运动使弹后的空间增大,又起到降低压力的作用,以上两种对立过程的净效应,使膛内压力开始上升,达到一定峰值时又呈下降趋势[3]。故由内弹道机理可知,挤进速度较小导致工况1的弹后空间增大速度趋缓,火药燃烧更加剧烈,必使其膛压较工况2增加迅速。

图6 弹丸加速度曲线图Fig.6 Acceleration of the projectile

图7 弹丸速度曲线图Fig.7 Velocity of the projectile

图8 阳线起点处Von Mises等效应力曲线图Fig.8 Von Mises Equivalent stress of the starting point of rifle line

图9 阳线起点处法向力曲线图Fig.9 Normal force of the starting point of rifle line

图10 阳线起点处剪切力曲线图Fig.10 Shear force of the starting point of rifle line
同工况2相比,坡膛长度过短使工况1具有高膛压、较大变形阻力、摩擦阻力及较慢的挤进速度,以上因素使工况1的坡膛内壁承受相对恶劣的受力环境。图8所示为挤进过程坡膛阳线起点处单元积分点的等效Von Mises应力图,可知工况1阳线起点处的等效应力远大于工况2。提取图5所示坡膛阳线起点处的节点法向力及由挤进摩擦所引起的剪切力,如图9、图10所示,在完全挤进时工况1、2于所选点处法向力及剪切力均达到峰值,且工况1峰值远大于工况2。由于任何材料在制造过程中都难免存在缺陷,如在微观尺度下的微裂纹、微孔洞等。在弹带挤进、冲击坡膛的过程中,坡膛材料固有的缺陷受载荷的作用而演化,特别是坡膛表面的微裂纹在其表面受到较大的剪应力作用时张开、扩展及合并,最终萌生垂直于挤进方向的宏观横向裂纹。
5 结论
本文对某大口径火炮及其改进型的弹带挤进冲击坡膛的过程进行了分析,运用弹塑性有限元接触理论并引入累计损伤失效机理对弹带挤进、冲击坡膛的动力学过程进行了建模和求解。通过分析计算明确了不同坡膛结构下弹带及弹丸的动力学响应,并计算分析了坡膛的长度对内弹道环境及坡膛受力的影响,为进一步深入研究坡膛横向裂纹的萌生及扩展提供了方向。但是对弹带挤进、冲击坡膛的有限元计算结果的应用还需要通过相关实验来验证。由于目前实验条件及测试手段的限制,弹带在高温、高压及瞬态的环境下冲击坡膛的实验研究和验证工作仍有一定难度。
[1]E.B.丘尔巴诺夫.挤进时期内弹道学与挤进压力计算[M].杨敬荣,译.北京:国防工业出版社,1997.
[2]刘俊红,傅苏黎,许世蒙.自润滑弹带接触应力问题的初步计算[J].装甲兵工程学院学报,2003,17(2):63-66.
[3]张喜发,卢兴华.火炮烧蚀内弹道学[M].北京:国防工业出版社,2001.
[4]金志明,曾思敏.弹丸挤进过程的计算与研究[J].兵工学报,1991,(1):7-13.
[5]吴志林,孔德仁.计及挤进过程的双头弹膛内运动模型[J].火炮发射与控制学报,2000,(1):9-14.
[6]张 浩,周彦煌.埋头弹火炮挤进过程研究[J].弹道学报,2006,18(1):76 -79.
[7]Hillerborg A,Modeer M,Petersson P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J].Cement and Concrete,1976,6:773-782.
[8]Hibbitt K,Sorensen,Sorensen,Inc.ABAQUS Theory Manual,Version 6.6[M].HKS Inc.,Pawtucket,Rhode Is-land,USA,2006.

