硫化矿石自燃灾害的脆性风险源

刘 辉，吴 超，李孜军，阳富强

(中南大学 资源与安全工程学院，国家金属矿安全科学技术研究中心，湖南 长沙，410083)

矿石自燃是硫化矿床开采中经常遇到的重大灾害之一。我国有大约30%的有色金属矿山、10%的铁矿山(主要是硫铁矿)、10%的非金属建材矿山存在矿石自燃的隐患[1-4]。据报道，自建国以来，已有数十座金属矿山发生过规模不一的硫化矿石自燃火灾，如江西瑞昌武山铜矿、广西大厂锡矿、安徽马鞍山向山硫铁矿、安徽铜陵铜官山铜矿等。硫化矿石自燃会引发一系列的安全与环境问题，并造成巨大的经济损失[2]。随着我国矿产资源不断向深部开发，深部开采面临的高温问题更加剧了高硫矿石开采过程中自燃事故的频发。目前，对于引发硫化矿石自燃事故的致灾因子，国内外还没有太多的研究。Wu等[5]在1995年运用系统安全分析法，对矿石自燃事故建立事故树分析，揭示矿石自燃必须是矿石具有氧化性、矿石与湿空气充分接触和矿石堆能聚热升温这3个事件同时发生并且当矿石堆的温度到达矿石冒烟(着火)时才发生，并就控制矿石自燃提出了可行方案。然而，由于井下作业空间的复杂性，含硫矿石自燃事故的引发具有明显的不确定性和随机性；因此，如何通过对自燃灾害事故进行客观、有效地分析，找出引发自燃事故的致灾因子及其相互影响关系，从而控制矿石自燃乃至从根本上杜绝自燃火灾的发生成为矿山安全科学迫切需要解决的重大课题。近年来，一些学者运用脆性理论[6-9]研究复杂系统，并且成功地应用于传染病扩散[7]、交通系统[8]等的研究中。荣盘祥等[6]根据脆性的定义以及脆性所具备的特性提出脆性熵和脆性联系熵函数等概念来研究复杂系统的特性及其与内、外不确定因素之间的关系。金鸿章等[8]描述了煤矿系统内部的脆性过程。井下硫化矿石堆所处空间是一个典型的复杂系统，其井下开采的作业环境与条件完全具有复杂系统所具备的特点。

1 复杂系统脆性

1.1 自燃灾害脆性的本质

含硫化物的矿床一旦被坑道工程揭露，氧化作用就不可避免。即使井下的温度为常温状态，在井下蓄热的空间环境，随着氧化的进行，矿石的温度也可逐渐增高，而温度的升高使其氧化产物(如 H2SO4或Fe2(SO4)3等)进一步加快氧化速度，当氧化作用所不断聚集的热量远远大于逸散的热量时，矿石自燃。自燃灾害的发生是矿石本身特性及其外在环境条件共同作用的结果，其易氧化的特性与井下容易蓄热的空间环境相互耦合，形成一个复杂的自燃灾害系统。研究结果表明，灾害是孕灾环境(E)、致灾因子(H)、承载体(S)综合作用的复合体系(D)，即D=E∩H∩S，其作用结构如图1所示[10]。如果系统由于受到内、外干扰因素的作用而使得某一部分发生崩溃，其他部分受到直接或间接的影响，进而引发崩溃，这样会带来连锁反应。金鸿章等[6]把系统的这种特性称之为脆性。

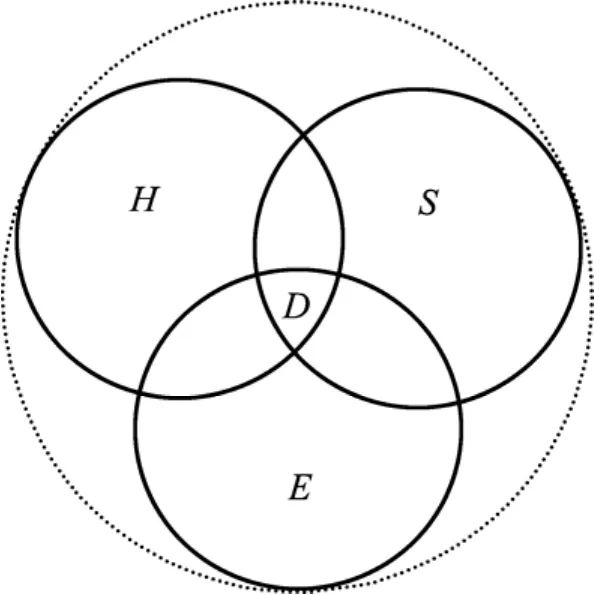
图1 灾害系统的作用结构Fig.1 Function system of disaster system

1.2 脆性关联

根据集对分析理论[11]，在复杂系统的子系统之间或子系统的各个要素之间，按照其功能和状态受相关系统(要素)崩溃影响的程度，可将脆性关联关系分为同一、波动和对立3种关系[6,11]。

集对分析的核心思想是将2个具有一定联系的集合组成1个集对，再在一定的环境条件下，分析集对所具有的特性。目前，集对分析法已经在科学研究、工程技术、哲学、社会科学、经济等领域得到初步的应用，并展现了广阔的发展前景。集对分析针对同、异和反3种不同的集对特性，建立其联系式为：

式中：a为同一性测度(同一度)；b为波动性测度(波动度)；c为对立性测度(对立度)；i和j分别为波动度、对立度系数，且i∈[-1, 1], j∈[-1, 0]，其取值可根据实际情况来定。

1.3 脆性联系熵

根据Shannon的信息熵理论，将系统抽象为n个事件进行分析，当每个事件出现的概率分别为 pi(i=1,2, …, n) 时，其选择结果的不确定程度可记为H(p1, …, pn) ：

结合集对分析方法，若一个子系统X在干扰下发生崩溃，则另外一个子系统Y的状态向量中至少有1个yj(1＜j＜n)与子系统X发生脆性同一、脆性波动和脆性对立的概率分别是pa(yj/X)，pb(yj/X)和pc(yj/X)，相应的脆性同一熵、波动熵和对立熵分别为[6]：

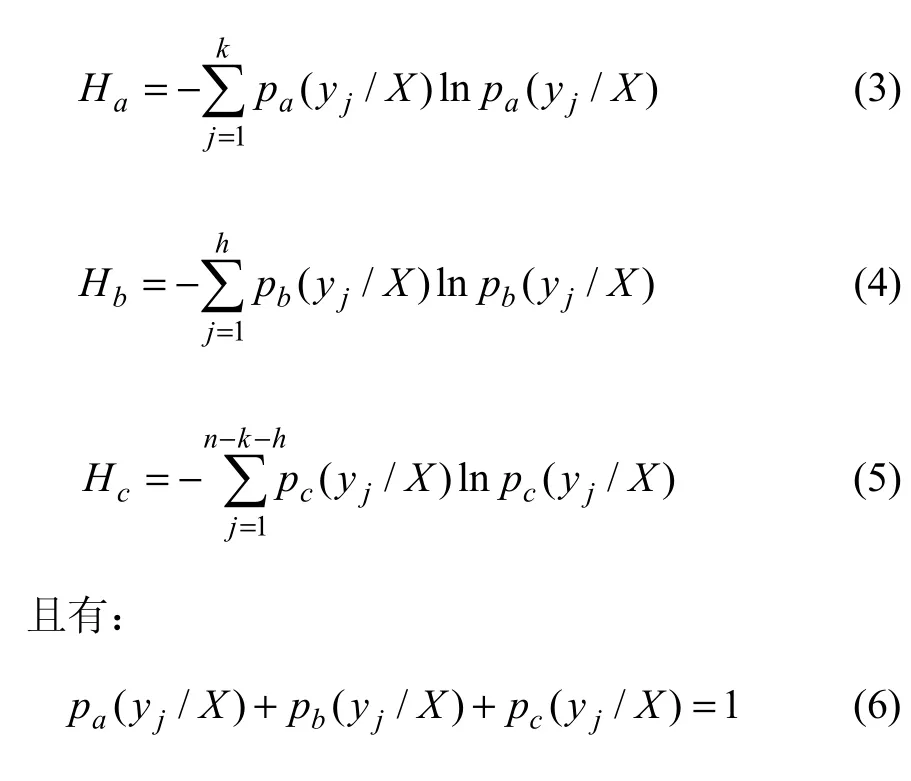
受X的影响，子系统Y是脆性同一、脆性对立和脆性波动的综合。因此，X崩溃发生时，子系统Y也发生崩溃的脆性联系熵为：

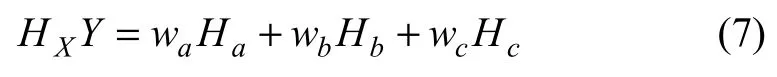
式中：wa, wb和wc分别为脆性同一、脆性对立和脆性波动的权系数。当存在一定的概率分布的组合，使HXY达到最大的情况时，子系统Y受到X崩溃的影响最大。

2 矿石自燃灾害的脆性风险源

系统是具有某种相互作用的若干要素的复合体。系统的要素之间存在着复杂的耦合关系，使系统在整体上具有涌现性；另外，系统又存在于一定的环境中，它与环境进行物质、能量和信息的交换，因此，环境又和系统构成一种密不可分的关系[12]。以承载体(S)作为研究对象，从致灾系统(H)、孕灾环境(E)建立矿石自燃灾害与结构模块的脆性关联，有：

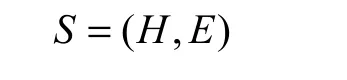
2.1 致灾系统

硫化矿石自燃与硫化矿物本身的物化性质密切相关[2,4]。由于硫化矿物中硫、铁元素各自的化学性质及相应的可变化合价，使得硫与铁的结合形式多样，所形成的化合物氧化还原性质也不同。从水溶液中铁离子含量、矿物成分的 TS(TS为某种硫化矿中各种硫化矿物成分的综合危险指标)等方面[13-14]提取脆性因子：

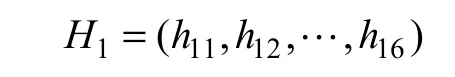
其中：h11为矿石氧化增重率，%(限期1月)；h12为水溶液中铁离子含量，%；h13为矿堆中水溶液的 pH；h14为矿物成分的TS；h15为初始自热温度，℃；h16为矿石的着火点，℃。

2.2 孕灾系统

井下封闭半封闭的空间与恶劣的作业环境是矿石蓄热的温床。自燃事故的统计分析表明，恶劣的现场作业环境空间是导致矿石自燃灾害频发的一个重要原因[2]。矿石堆能蓄热升温是由于矿石堆散热条件差、堆放时间长以及通风不良等引起。其脆性因子可取为：

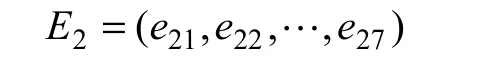
其中：e21为选用的采矿方法；e22为矿石损失率，%；e23为通风条件；e24为矿岩环境温度，℃；e25为矿堆体积；e26为堆放时间，d；e27为地质构造特征。

2.3 脆性关联分析模型

依据致灾、孕灾系统的脆性因子与矿石自燃灾害可能存在的脆性同一性、脆性波动性和脆性对立性等关系建立井下硫化矿石自燃灾害的脆性关联分析模型，如图2所示。

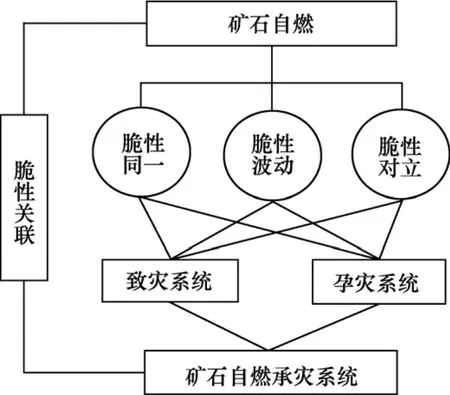
图2 脆性关联分析模型Fig.2 Brittle relational analysis model

3 工程实例

3.1 工程概况

安徽某矿是目前已发现的国内埋藏最深的特大型高硫铜矿。根据矿体赋存条件，该矿主要采用大直径垂直深孔落矿以及上向扇形中深孔落矿的阶段空场嗣后充填采矿方法，其矿床的矿石工业类型主要为铜硫矿石，占83.08%，其次为单硫矿石，占14.995%，再次为铜铁矿石，占1.93%。矿石平均含硫约17%，最高处达19%。该矿区恒温带深度为(20±5) m，恒温带温度为17.55 ℃。平均地热增深率为2.1 ℃/m，矿床所处层位的原岩温度在30～39.8 ℃之间变化，属于典型的高温高硫金属矿床。

3.2 数据采集与处理

综合我国多个硫化矿山的实际情况，分别对引发矿石自燃灾害的各脆性因子进行测度分级，其分级标准[13-14]如表1所示。通过采集现场及实验数据并就具体生产情况进行分析，获得各脆性因子的测度调查结果，并根据表1中的脆性测度分级标准，获得各脆性因子的脆性关联性，具体结果如表2所示。为更好地阐述这一方法及方便计算，取该矿硫化矿石自燃灾害与致灾系统及孕灾系统相关因素发生脆性同一、脆性波动及脆性对立的概率为相应的脆性测度，计算结果见表3。

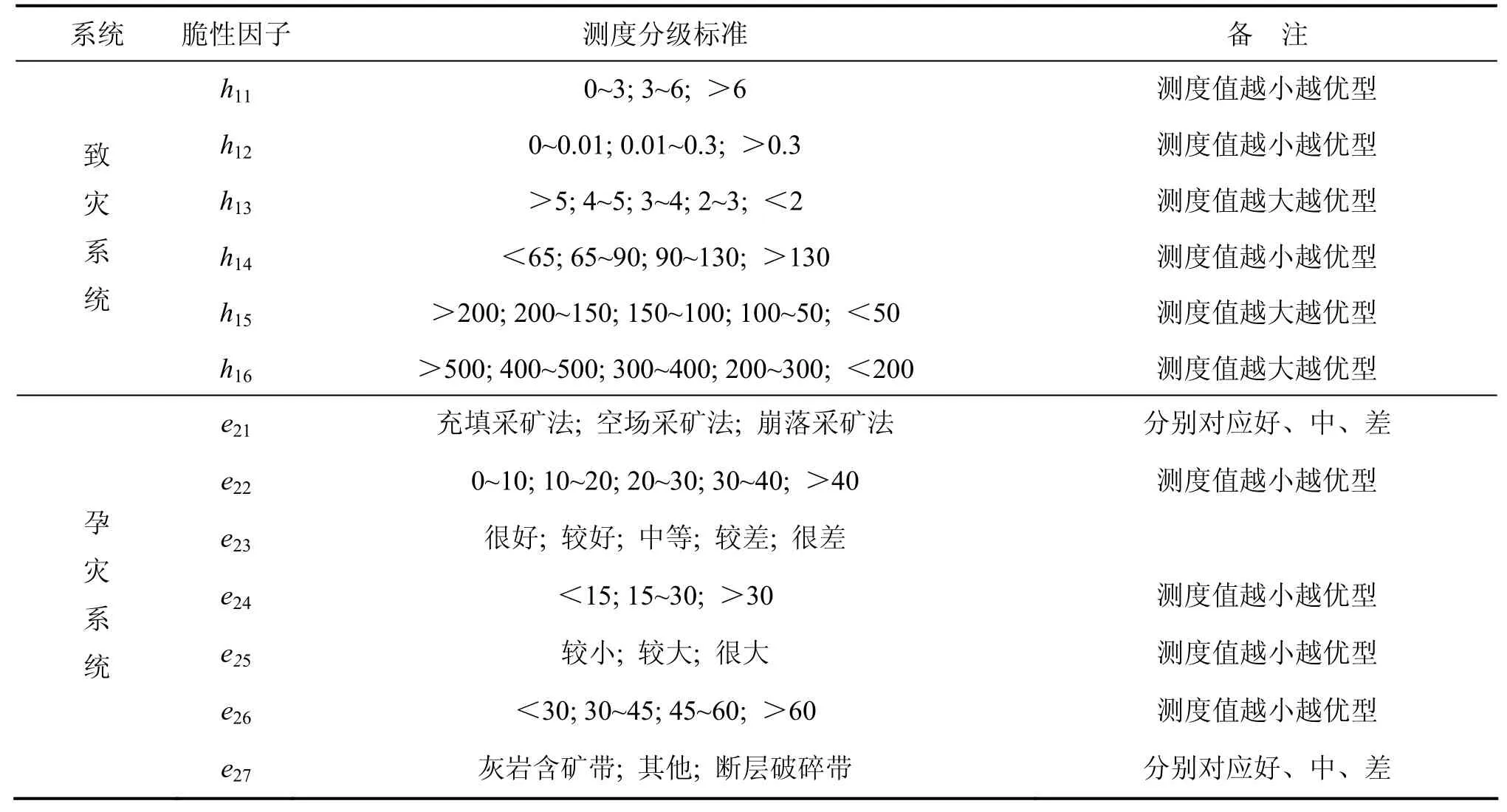
表1 相关系统脆性因子测度分级标准Table1 Grading rules of corresponding measures of brittleness

3.3 权系数确定

式(7)脆性联系熵中的权系数，可以根据其同一熵、波动熵和对立熵对井下自燃事故承灾系统发生变化所起的作用来确定。参照文献[6]，采用突变级数法确定各个权系数[15]。托姆提出一系列数学模型，用以解释自然界和社会现象中所发生的不连续的变化过程，描述各种现象为何从形态的一种形式突然地飞跃到根本不同的另一种形式，并已证明，当控制变量不大于4个时，最多有7种突变模型[6]。其中燕尾突变的势函数为：

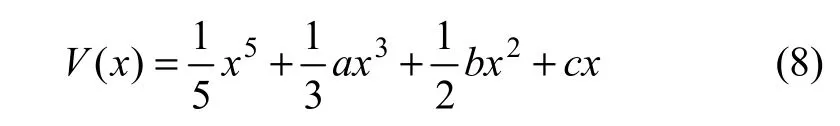
式中：a，b和c为控制变量；x为状态变量。其分解形式的分歧集方程为：

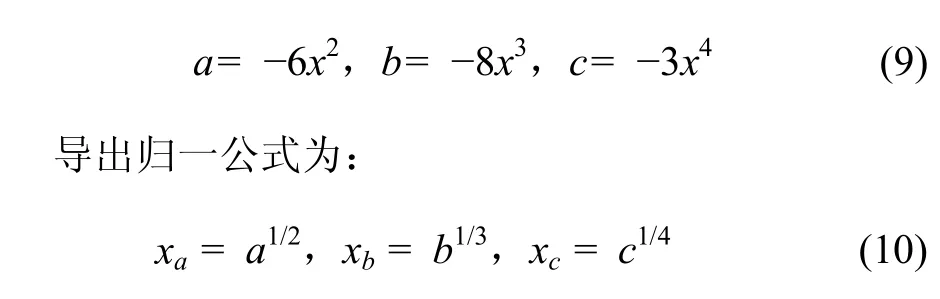
式中：x, a, b, c的取值范围在0, 1之间；wa, wb和wc分别取xa, xb和xc。

结合式(1)，(3)，(4)及(5)，分别求得各子系统脆性熵如表4所示，其中取j = -1 , i∈[0, 1]。

3.4 结果分析

从表4可以看出：当i取1时，矿石自燃灾害的发生与各系统间脆性联系熵的最大值分别为max(H)=0.088 6；max(E)=0.139 6。数据显示孕灾系统与事故的最大脆性关联度比致灾系统的大。这说明就该矿山的实际情况而言，其矿体赋存条件下矿石具有的氧化自热性固然是自燃事故发生的内在因素，然而，对于其自燃事故的发生起最终作用的还是井下复杂的孕灾环境，从表4也可以看出，致灾系统与硫化矿石自燃的发生具有同一性的熵为0，而孕灾系统达到0.278 1。这也从本质上反映了含硫化物的矿床一旦被坑道工程揭露，氧化作用就不可避免，而井下蓄热的环境终将促发矿石自燃灾害。

由脆性熵理论可知，事故的脆性熵反映了矿石自燃灾害发生的不确定性程度，熵越大，灾害事故发生的风险就越大，因此，避免硫化矿床开采中矿石自燃灾害脆性的根本方法在于从外界引入负熵来抑制系统内部的熵增。从2个系统的波动熵值情况来看，Δ(BE)＞Δ(BH)，可见孕灾系统对应的脆性波动熵最大，其对系统发生熵变的影响也就最大；所以，在具有自燃倾向性的硫化矿床开采中，选用的采矿方法、矿石损失率、堆积时间及通风条件等是决定与控制矿山自燃灾害事故发生的关键。

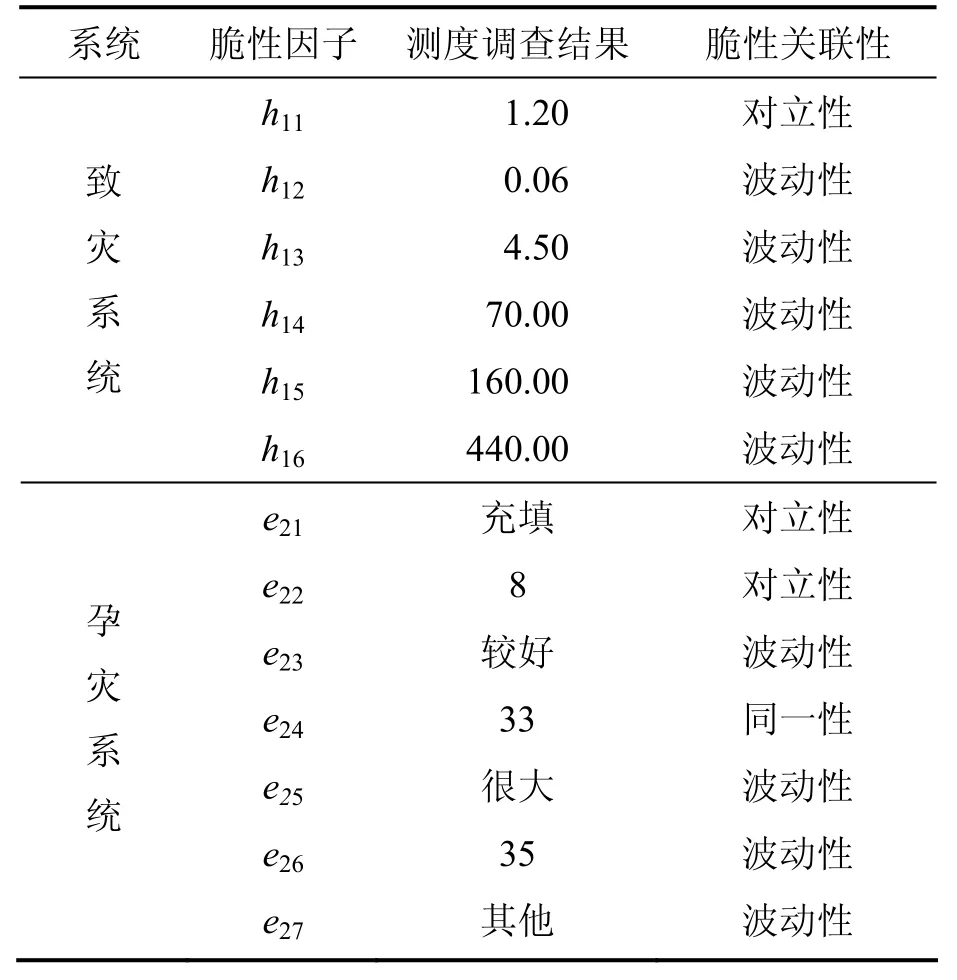
表2 现场调查结果及各因子脆性关联性Table2 Investigation results and brittle relations between factors and accident

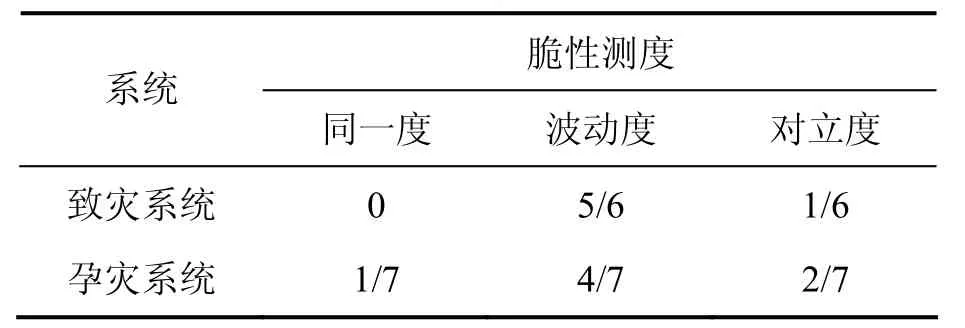
表3 相关系统对应的脆性测度Table3 Corresponding measures of brittleness

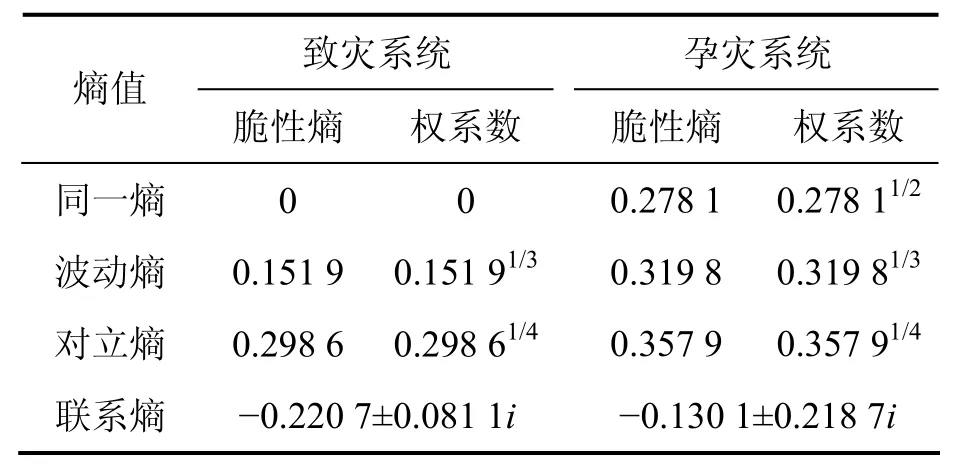
表4 相关系统脆性熵值及权系数Table4 Corresponding brittleness entropies and weighty coefficients

4 结论

(1) 硫化矿石自燃灾害的发生是矿石本身特性及其外在环境条件共同作用的结果，矿石易氧化的特性与井下容易蓄热的空间环境相互耦合，形成一个复杂的自燃灾害系统。

(2) 基于脆性理论，建立了硫化矿石自燃灾害脆性关联分析模型，并根据自燃矿石的物理化学等特性及矿山井下开采的条件，提出致灾系统脆性因子为：矿石氧化增重率、水溶液中铁离子含量、矿堆中水溶液的pH、矿物成分的综合危险指标、初始自热温度、矿石的着火点；孕灾系统脆性因子为：采矿方法选择、矿石损失、通风条件、矿岩环境温度、矿堆体积、堆放时间、地质构造特征。

(3) 安徽某高硫铜矿作业方法与环境是构成矿石自燃事故承灾系统脆性的根本原因；在开采具有自燃倾向性的含硫化物的矿床中，通过选用合理的采矿方法，减少矿石损失率及堆积时间，改善矿井通风等条件来破坏井下蓄热的环境是控制矿石自燃灾害事故发生的有效措施。

[1] 李明, 吴超, 李孜军. 多因素耦合条件下硫化矿自燃神经网络动态预测模型研究[J]. 中国安全科学学报, 2007, 17(8):32-36.

LI Ming, WU Chao, LI Zi-jun. Research on ANN dynamic prediction model for spontaneous combustion of sulfide ores with multi-factors coupling[J]. China Safety Science Journal,2007, 17(8): 32-36.

[2] 李孜军. 硫化矿石自燃机理及其预防关键技术研究[D]. 长沙:中南大学资源与安全工程学院, 2007: 1-3.

LI Zi-jun. Investigation on the mechanism of spontaneous combustion of sulfide ores and the key technologies for preventing fire[D]. Changsha: Central South University. School of Resource and Safety Engineering, 2007: 1-3.

[3] 刘辉, 吴超, 潘伟, 等. 硫化矿石堆自燃早期指标优选及预测方法[J]. 科技导报, 2009, 27(3): 46-50.

LIU Hui, WU Chao, PAN Wei, et al. Index optimization and forecast model of spontaneous combustion of sulfide ore dump during early stage[J]. Science and Technology Review, 2009,27(3): 46-50.

[4] WU Chao, LI Zi-jun, ZHOU Bo. Coincidence on relevant substances of sulfide ores in the oxidation process at ambient temperature and a new method for predicting fire[J].Transactions of Nonferrous Metals Society of China, 2004, 14(1):33-37.

[5] WU Chao. Fault tree analysis of spontaneous combustion of sulphide ores and its risk assessment[J]. Journal of Central South University of Technology, 1995, 2(2): 78-80.

[6] 荣盘祥, 金鸿章, 韦琦, 等. 基于脆性联系熵的复杂系统特性的研究[J]. 电机与控制学报, 2005, 9(2): 111-115.

RONG Pan-xiang, JIN Hong-zhang, WEI Qi, et al. Research on the characteristic complex system based on brittle link entropy[J].Electric Machines and Control, 2005, 9(2): 111-115.

[7] 韦琦, 金鸿章, 姚绪梁, 等. 基于脆性的复杂系统崩溃的初探[J]. 哈尔滨工程大学学报, 2003, 24(2): 161-165.

WEI Qi, JIN Hong-zhang, YAO Xu-liang, et al. Collapse of complex system based on brittleness[J]. Journal of Harbin Engineering University, 2003, 24(2): 161-165.

[8] 金鸿章, 吴红梅, 林德明, 等. 煤矿事故系统内部的脆性过程[J]. 系统工程学报, 2007, 22(5): 449-454.

JIN Hong-zhang, WU Hong-mei, LIN De-ming, et al. Interior brittleness process of coalmine accident system[J]. Journal of System Engineering, 2007, 22(5): 449-454.

[9] Lind N C. A measure of vulnerability and damage tolerance[J].Reliability Engineering & System Safety, 1995, 48(1): 1-6.

[10] 史培军. 四论灾害系统研究的理论与实践[J]. 自燃灾害学报,2005, 14(6): 1-7.

SHI Pei-jun. Theory and practice on disaster system research in a fourth time[J]. Journal of Natural Disasters, 2005, 14(6): 1-7.

[11] 赵克勤. 集对分析与熵的研究[J]. 浙江大学学报, 1992, 6(2):69-73.

ZHAO Ke-qin. Study entropy based on the set pair analysis[J].Journal of Zhejiang University, 1992, 6(2): 69-73.

[12] 赵金宪, 金鸿章, 吴红梅. 煤矿瓦斯爆炸事故的脆性风险源分析[J]. 黑龙江科技学院学报, 2008, 18(4): 262-265.

ZHAO Jin-xian, JIN Hong-zhang, WU Hong-mei. Brittleness risk source analysis for mine gas explosion[J]. Journal of Heilongjiang Institute of Science & Technology, 2008, 18(4):262-265.

[13] WU Chao, XIA Chang-nian, LI Zi-jun. Safety assessment system for evaluating spontaneous combustion of sulfide ores in mining stope[C]//Proceedings of the 2006 International Symposium on Safety Science and Technology. Changsha, 2006:1599-1604.

[14] 高科, 李明, 吴超, 等. 突变级数法在硫化矿爆堆自燃发火预测中的应用[J]. 金属矿山, 2008(2): 20-34.

GAO Ke, LI Ming, WU Chao, et al. Application of catastrophe progression method in forecasting spontaneous combustion of blasted muck pile of sulfide ore[J]. Metal Mine, 2008(2): 20-34.

[15] 朱顺泉. 基于突变级数法的上市公司绩效综合评价研究[J].系统工程理论与实践, 2002, 22(2): 90-94.

ZHU Shun-quan. Study on catastrophe theory and application of credit evaluation of listed corporation[J]. System Engineering Theory and Practice, 2002, 22(2): 90-94.