随机参数时变齿轮副的动力响应分析

魏永祥，陈建军，拓耀飞

(1. 西安电子科技大学 机电工程学院，陕西 西安，710071；2. 榆林学院 物理与电气工程系，陕西 榆林，719000)

齿轮系统应用于多种机械动力装备中传递运动或动力。在各种机械特别是精密机械中，都要求降低齿轮传动引起的振动和噪声。由于材料属性、加工精度和负载状况等因素，齿轮系统在工作过程中经常会出现振动加剧或突变，导致磨损、疲劳破坏和大噪声，从而使机器工作的可靠性和性能降低，甚至使系统遭到破坏。因此，有必要研究齿轮啮合的动态位移及其各参数对动态位移的影响等问题。当考虑齿轮时变啮合刚度时，系统的动力学模型将是一个具有周期性时变系数的非线性系统[1]。对于时变刚度的齿轮系统，很多学者在确定性齿轮系统的响应及稳定域方面做了大量的工作。张永忠等[2-4]研究了齿轮在啮合过程中有关齿轮刚度、齿根应力的计算方法和具有时变啮合刚度的齿轮系统的动力学问题。唐增宝等[6-8]分别用不同的方法求解了齿轮系统的时变非线性微分方程，获得了系统的动态响应，分析了不同因素对齿轮振动响应的影响。然而，这些文献都是以确定性的齿轮系统为研究内容。近年来，人们开始关注齿轮的随机动力响应问题，如：Wang等[9-11]考虑了随机(模糊)误差激励或在随机外激励下，时变刚度齿轮传动系统的动力响应，然而，并未考虑齿轮系统中物理和几何参数的随机性对其动力响应的影响。在实际中，由于材料属性的随机性和在加工、安装过程中的多种随机因素的影响，都会造成齿轮系统动力响应的随机性。Chen等[12-14]应用随机因子法处理了具有随机参数结构的动力响应问题。在此，本文作者以随机参数时变刚度齿轮副为分析模型，在考虑弹性模量、质量密度、齿宽和模数等系统参数同时具有随机性且作用荷载幅值也具有随机性的情况下，利用Duhamel积分[15]，分析随机参数时变刚度齿轮副在随机力激励下的动力响应的数字特征。

1 确定性齿轮动力分析模型

对直齿圆柱齿轮副，当支撑轴承和传动轴的刚度比轮齿啮合刚度大许多时(即可认为是刚性的)，单级齿轮副传动系统的动力学简化模型如图1所示。其中：PQ为齿轮理论啮合线；Ri，Ii，θi和Ti(i=1, 2)分别为啮合齿轮的基圆半径、转动惯量、扭转角和所承受的转矩。该模型的动力学方程为[5]：

式中：iθ，(i=1, 2)分别为主动齿轮和被动齿轮的扭转角、角速度和角加速度；Ii(i=1, 2)为主、被动齿轮的转动惯量；Ri(i=1, 2)为主动齿轮和被动齿轮的基圆半径；ki和ci(i=1, 2)分别为主动齿轮和被动轮齿的挠曲刚度和阻尼；ei(i=1, 2)为主动齿轮和被动轮齿的综合误差；Ti(i=1, 2)为作用在主动齿轮和被动齿轮上的力矩；km(t)和cm分别为齿轮副的啮合刚度和啮合阻尼。其中单齿啮合时的刚度 k(t)采用魏氏挠度公式和两圆柱接触变形的赫兹公式[2]进行计算，即：

式中：kc为轮齿在啮合点的接触刚度。

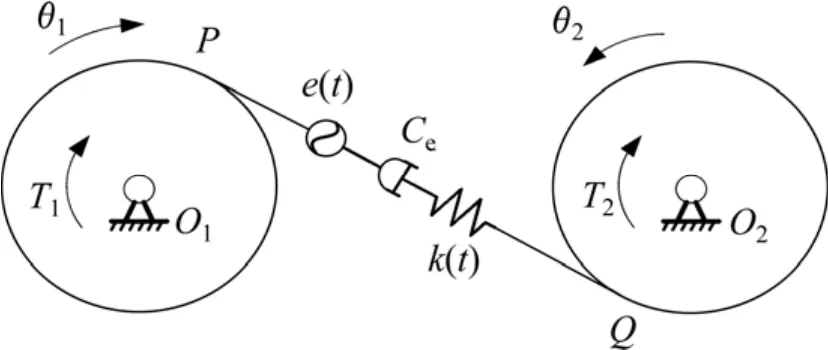
图1 单级齿轮副物理模型Fig.1 Physical model of one-stage gear

由于k1，k2和kc在不同啮合点处的取值不同，且单齿或多齿交替啮入啮出会导致刚度突变，因此，啮合刚度km(t)为时变刚度。将单齿啮入到啮出作为1个研究周期，并把这1个周期n等分后逐步计算不同啮合点的刚度，最后根据重合度判断不同啮合点处是单齿或是多齿啮合来计算总的时变啮合刚度。

对啮合阻尼cm由下式计算[5]：

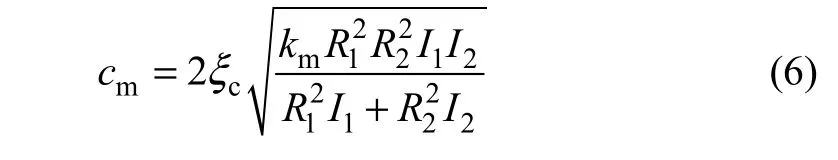
其中：ξc为轮齿啮合的振型阻尼比。

记啮合线上两齿轮的相对位移为x，即有：

其中：me为等效质量；P为等效载荷。

由于齿轮啮合时齿间间隙很小，故将齿轮副等效为2个等厚薄圆柱，且其质量密度相同，它们的转动惯量分别为：

其中基圆半径由下式得：

式中：z1和z2分别为主动齿轮和被动齿轮的齿数；α为压力角。

2 随机参数时变刚度齿轮副在随机力激励下的响应分析

利用 Duhamel积分可求得系统动力学方程(8)的形式解为：

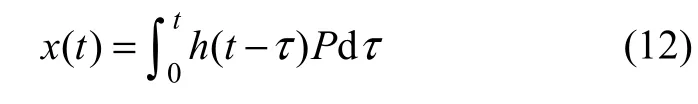
其中：τ为时间积分变量；h(t)为系统的脉冲响应函数，即有

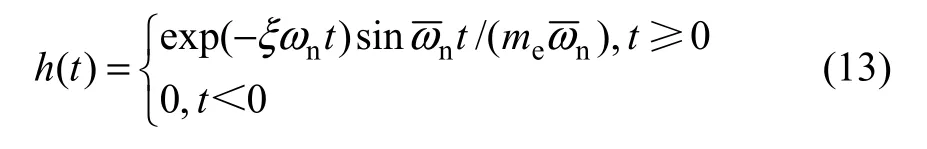
现考虑系统参数具有随机性的情况。设齿轮副的材料相同，其物理参数(弹性模量E和质量密度ρ)和几何参数(齿宽b，模数mo= s /π，s为相邻两轮齿同侧齿廓间的齿距)同时为随机变量。模数虽已标准化，但由于制造、装配等因素都会导致齿距s仍有随机性，从而使模数也有随机性。则由以上推导公式可知，齿轮啮合系统的等效啮合刚度 km(t)和等效质量 me亦为随机变量。显然，这将导致系统固有频率ωn的随机性，进而导致系统响应的随机性。下面导出系统位移响应的数字特征计算表达式。

利用求解随机变量函数数字特征的矩法，从式(12)出发，可求得系统位移响应的均值和方差分别为：

式中：μ和σ分别为随机变量的均值和均方差。

以下导出求式(14)和(15)中所需的计算表达式。

首先将式(10)和(11)代入式(9)，经整理并利用随机因子法[12]得：

利用求解随机变量函数的代数综合法，由式(16)可推得随机变量me的均值μme和方差分别为：

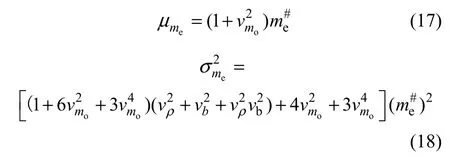
由动力学中的瑞利商公式，系统的固有频率nω可写成随机因子的形式如下：

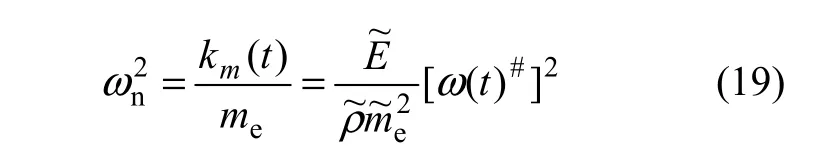
同样，由式(19)可推得系统固有频率ωn的均值μωn和均方差σωn分别为：

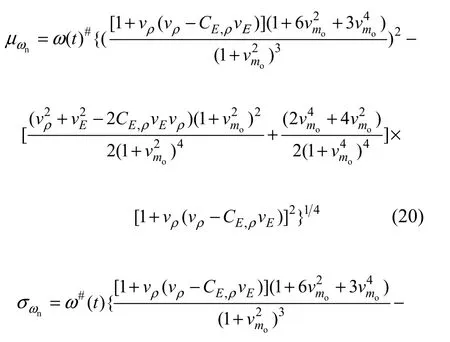
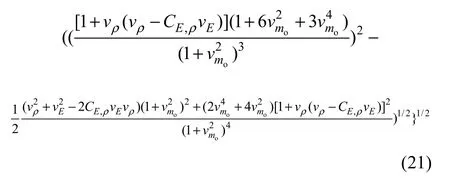
其中：ρ,EC为E和ρ的相关系数。

将以上导出的计算式(16)～(21)代入式(14)和(15)，即可获得随机时变齿轮副动力响应的数字特征。

3 算例

依据上述导出的计算公式和Duhamel数值积分方法，编制了计算随机参数时变刚度齿轮副的动力响应分析程序。取标准圆柱齿轮副，材料为钢。齿数z1=45，z2=100，压力角α=20°，齿轮的额定转速为 2 000 r/min，阻尼系数 ξ=0.003，泊松比 μ=0.2，变位系数 χ=0。考虑材料的弹性模量E、密度ρ、齿宽度b、模数mo和荷载P均为随机变量，它们的均值分别为：μE=2.08×1011Pa，μρ=7.86 t/m3，μb=16 mm，μmo=4 mm，μP=795.78 N。为比较各随机参数取值的分散性对系统的影响，它们的变异系数均取为0.1。

图2所示为单齿啮合4倍个啮合周期T(单齿从啮入到啮出的时间)内啮合刚度的变化曲线。经计算得齿轮啮合的重合度为1.794 2，即在1个啮合周期T内，0.794 2T的时间处于双齿啮合区，0.205 8T的时间为单齿啮合区。在不同啮合点处刚度不同，且单齿与双齿交替啮入和啮出时导致刚度突变。

图2 齿轮时变刚度Fig.2 Time-varying stiffness of gear

图3 所示为根据计算结果按“3σ”准则绘出的随机时变齿轮副的动态位移响应(此处的位移是指两齿轮轮齿啮合处的相对变形量)的均值μ和上下界μ±3σ的波动曲线。图中的横坐标是以轮齿啮合周期(单齿从啮入到啮出的时间)T的倍数。从图 3可看出：在0.794 2T单双齿交替啮合时由于刚度突变引起的位移冲击响应；位移的均方差也随时间变化，且在单齿啮入时动态位移响应的分散性变大。刚度突变对动态位移响应的均方差与对均值的影响趋势相一致。

图3 随机动态位移响应Fig.3 Stochastic dynamic displacement response

图4 所示为考虑随机时变齿轮副系统参数全部为随机变量时的动态位移均值与参数为确定性时动态位移的对比。从图4可以看出系统参数的随机性对动态位移的均值也有影响。

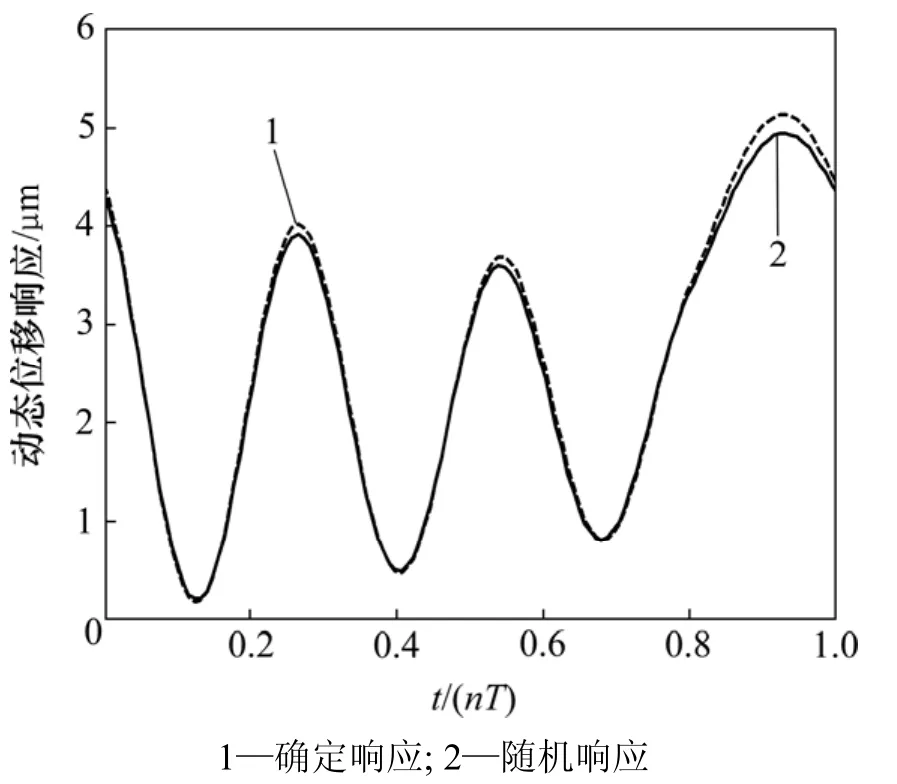
图4 随机和确定模型的动态位移响应Fig.4 Random and determine model of dynamic displacement response

为考察各个随机参数的分散性对系统响应的影响，表1列出了不同随机参数组合时系统的最大位移响应的均值和均方差。结果表明：当参数全为随机变量时位移响应均值的分散性最大，与确定模型相差也最大。其中：弹性模量E和密度ρ的随机性对位移响应的均值影响相反，但对方差的影响却基本相一致；齿宽b的随机性对位移响应的影响很小；荷载P的随机性对位移响应的均值基本没有影响，却对方差的影响起主导作用；模数mo的随机性对位移响应方差的影响也很大，其影响仅次于荷载P的影响；模数mo的随机性主要反映了齿轮的分度圆半径的随机性对位移响应的影响。

表1 不同随机组合时系统的最大位移位移响应的均值和均方差Table1 Mean and variance of effect of different random combinations of maximum displacement response of system

4 结论

(1) 当考虑齿轮副的物理和几何参数具有随机性时将导致系统的刚度、质量和固有频率也有随机性，使动力方程成为随机微分方程，常规的动力分析方法将无法求解，只能用概率的分析方法。当随机性模型中各随机变量的变异系数均为0就变为确定性模型，后者仅是前者的特例。

(2) 齿轮副参数的随机性对系统位移响应的均值有一定的影响，荷载的随机性对系统位移响应的均值没有影响，却对系统位移响应的均方差的影响很大。齿轮的几何参数(特别是模数mo)的随机性对系统位移响应的影响不可忽略；因此，齿轮副的加工精度对齿轮副的动力响应的随机性具有重要作用。由于单齿双齿甚至多齿交替啮入啮出时将导致啮合刚度突变，在刚度突变时，系统的位移响应有冲击现象发生，系统响应的均方差也会出现突变。

(3) 本文计算所得的系统动力响应的数字特征可为开展随机参数齿轮系统的动力可靠性分析、预测和优化设计提供了必要的数据信息。

[1] 张锁怀, 孙玉杰, 沈允文. 齿轮时变系统的强迫振动[J]. 中国机械工程, 2005, 16(8): 723-728.

ZHANG Suo-huai, SUN Yu-jie, SHEN Yun-wen. Forced vibration of gear system with time-varying mesh stiffness[J].Chinese Mechanical Engineering, 2005, 16(8): 723-728.

[2] 张永忠, 王洪. 齿根动态应力分析[J]. 机械工程学报, 1986,22(3): 58-65.

ZHANG Yong-zhong, WANG Hong. The dynamic stresses analysis of tooth root[J]. Chinese Journal of Mechanical Engineering, 1986, 22(3): 58-65.

[3] Cai Y. Simulation on the rotational vibration of helical gears in consideration of the tooth separation phenomenon (A new stiffness function of helical involute tooth pair)[J]. Journal of Mechanical Design, ASME, 1995, 117(9): 460-468.

[4] Domain G. Solution of coupled nonlinear partial differential equations by decomposition[J]. Computer Math, Applic, 1996,31(6): 117-120.

[5] 李润方, 王建军. 齿轮系统动力学: 振动、冲击、噪声[M]. 第1版. 北京: 科学出版社, 1997: 1-247.

LI Run-fang, WANG Jian-jun. Dynamics of gear system:vibration, shock and noise[M]. 1st ed. Beijing: Science Press,1997: 1-247.

[6] 唐增宝, 钟毅芳. 直齿圆柱齿轮传动系统的振动分析[J]. 机械工程学报, 1992, 28(4): 86-93.

TANG Zeng-bao, ZHONG Yi-fang. The vibration analysis of a spur gear-transmission system[J]. Chinese Journal of Mechanical Engineering, 1992, 28(4): 86-93.

[7] Litak G , Friswell M I. Dynamics of a gear system with faults in meshing stiffness[J]. Nonlinear Dynamic, 2005, 41(4): 415-421.

[8] 欧卫林, 王三民, 袁茹. 齿轮耦合复杂转子系统弯扭耦合振动分析的轴单元法[J]. 航空动力学报, 2005, 20(3): 537-538.

OU Wei-lin, WANG San-min, YUAN Ru. Shaft element method for the analysis of lateral-torsional coupling vibration of a complex gear-rotor system[J]. Journal of Aerospace Power, 2005,20(3): 537-538.

[9] Wang Y, Zhang W J. Stochastic vibration model of gear transmission systems considering speed dependent random errors[J]. Nonlinear Dynamics, 1998, 17(2): 187-203.

[10] 马亮, 李瑰贤, 吴俊飞. 含有模糊参数的齿轮副动态响应分析[J]. 机械科学与技术, 2001, 20(2): 203-204.

MA Liang, LI Gui-xian, WU Jun-fei. Analysis of the gear pair dynamic response containing fuzzy parameters[J]. Mechanical Science and Technology, 2001, 20(2): 203-204.

[11] 刘梦军, 沈允文, 董海军. 随机外激励下齿轮非线性系统的全局分析[J]. 中国机械工程, 2004, 15(13): 1182-1185.

LIU Meng-jun, SHEN Yun-wen, DONG Hai-jun. Global analysis for the nonlinear gear system with stochastic external excitation[J]. Chinese Mechanical Engineering, 2004, 15(13):1182-1185.

[12] Chen J J, Che J W, Sun H A, et al. Probabilistic dynamic analysis of truss structures[J]. Structural Engineering &Mechanics, 2002, 13(2): 231-239.

[13] 戴君, 陈建军, 马洪波，等. 随机参数结构在随机荷载激励下的动力响应分析[J]. 工程力学, 2002, 19(3): 64-68.

DAI Jun, CHEN Jian-jun, MA Hong-bo, et al. Dynamic response of structures with random parameters under random loads[J].Engineering Mechanics, 2002, 19(3): 64-68.

[14] 陈建军, 黄居锋, 赵颖颖. 随机参数链式结构系统的动力特性分析[J]. 中国机械工程, 2005, 16(1): 16-19.

CHEN Jian-jun, HUANG Ju-feng, ZHAO Ying-ying. Dynamic characteristics analysis based on probability for random chain structures[J]. Chinese Mechanical Engineering, 2005, 16(1):16-19.

[15] Moser W, Antes H, Beer G. A duhamel integral based approach to one-dimensional wave propagation analysis in layered media[J]. Comput Mech, 2005, 35(2): 115-126.