盾构刀具破岩过程及其切削特性

夏毅敏，薛 静，周喜温

(中南大学 机电工程学院，教育部现代复杂装备设计与极端制造重点实验室，湖南 长沙，410083)

近年来，我国地铁工程建设正在高速发展，盾构隧道掘进机已越来越广泛地运用于地铁隧道的施工工程中。盾构机是盾构施工的主要设备，盾构刀盘刀具作为盾构机的开挖岩土部件，在盾构施工中起到非常关键的作用；因此，在研究刀具切削岩土的过程中，探讨盾构刀具的破岩机理、岩土的断裂机理显得尤为重要[1]。随着计算机技术的发展，数值化模拟技术已经广泛应用于岩石切削过程的研究[2-3]。目前，国内外学者已经采用多种数值分析方法用来模拟分析岩石切削机理，如：Korinets等[4]采用有限元方法(FEM)中的DIANA程序对盘形滚刀和球形平底压头挤压岩石所得破损量进行模拟；Carpanteri等[5]采用Franc2D软件对岩石的裂纹进行数值分析；Tan等[6]采用边界元分析方法模拟二维单压头和多压头滚压岩石时裂纹的形成；Kou等[7]利用东北大学开发的二维 RFPA程序，模拟刀具切削非均匀岩石介质逐渐破坏过程；Liu等[8]采用RFPA程序模拟单、双压头压碎岩石裂纹扩张的过程，并分析裂纹形成的机理；Gong等[9]通过 DEM方法中的DUEC程序模拟盾构滚刀破岩裂隙的产生过程。在刀具切削参数优化方面，目前对切削金属刀具的优化研究较多[10-12]，但对盾构刀具的研究较少。为此，本文作者在虚拟设计思想指导下，通过基于国际化通用大型有限元平台之上的数值仿真技术，针对一个简化的二维模型对刀具切削软岩时裂纹的产生、扩展和汇合过程进行分析。在盾构刀具切削过程中，借助有限元软件通过对三维模型的模拟分析，研究切削参数和刀具几何参数对切削的影响规律，以便为实现刀具几何参数和切削参数的优化奠定基础。

1 刀具-软岩接触的有限元模型

1.1 材料模型

有限元模拟的准确性在很大程度上取决于本构关系能否真实反映材料的特性。岩石材料是一种经过长时间地质作用以及受地质环境影响而形成的一种复杂介质，其内部不可避免地存在大小不一、形状各异的裂隙。在载荷作用下，变形非常复杂，不仅有弹性变形，而且有塑性、脆性断裂等复杂现象。在盾构施工过程中，当岩石受到刀具不断挤压作用而发生切削破碎时，岩体裂隙不断扩展演化，从而使其表现出复杂的应力-应变关系。而损伤力学就是从这些缺陷的不断劣化着手研究其应力-应变关系的一种有效手段。目前，损伤理论已经广泛用于钢筋混凝土材料、复合材料以及岩土材料的研究。本文在数值分析过程中，采用一种在 Ottosen四参数破坏准则基础上引入损伤因子的弹塑性本构模型，以便真实了解岩土的特性[13-14]。其本构模型为：

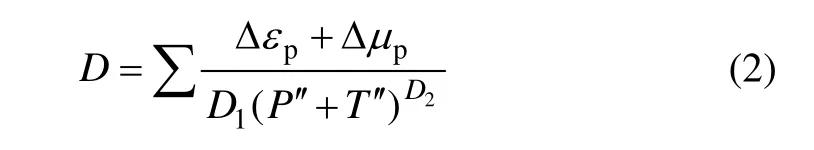
Δεp和Δµp分别为等效塑性应变、等效塑性体积应变；；T为材料能承受的最大静态拉伸压力；D1和D2为材料的损伤常数。

1.2 有限元模型的建立

建立如图1所示的二维、三维刀具切削岩石的有限元模型。为了减少求解时间，将刀具设为刚体，将岩石模型的网格划分为2部分：在岩石与刀具接触的区域划分较细，而远离接触的区域划分的网格相对来说就较粗。对刀具施加Y和Z方向的位移约束和约束3个方向的转动自由度。对于岩石材料，为了阻止边界产生的人工应力波反射重新进入模型影响仿真结果，对底面以及左表面采用非反射边界约束，前、后两面约束采用Z方向的平动和转动，右表面和上表面采用自由状态。对刀具施加速度载荷，切刀速度设为1 m/s，贯入度(即刀具切入岩石的深度)为6 mm。

图1 盾构切削切削软岩有限元模型Fig.1 Finite element models of shield cutter cutting soft rock

2 结果讨论与实验验证

2.1 切削裂纹的产生

通过单元的失效在结构中产生的裂纹来模拟破碎过程中岩石裂纹的生成和扩展趋势。在仿真过程中，要求在模型中产生裂纹的部位划分较密的网格；因此，为了减少计算时间，建立二维简化切削模型，如图 1(a)所示。这里选取某一岩块的前进破碎过程进行分析，如图2所示。求解完成后，利用后处理器对模拟结果进行分析，可以很直观地观察到盾构刀具切削软岩时裂纹萌生、扩展直到整个破坏的过程。

从力学机制上看，岩石破碎可以分为剪切破坏和拉伸破坏2种形式，它们各自有不同的破坏准则，本文采用最大抗拉强度理论和最大剪应力理论联合破坏准则。经分析可得：岩石的切削过程实际上是刀具的切削挤压作用，导致刀尖前区岩石矿物被压碎形成压碎域，压碎域周围产生微裂纹、断裂裂纹，形成粉屑、颗粒粉屑和断屑的循环过程。在刀具切削过程中，刀尖下端岩石因应力集中，会产生多条裂纹，一般只有1条或几条裂纹会因裂纹扩展而形成切屑，其他的裂纹留在岩石内部成为残留裂纹。在岩石压碎区形成之前，刀尖前端岩石因应力集中，沿岩石的最大主应力方向开始产生一系列微裂纹，如图 2(a)所示；随着刀具的继续前进，当极限拉应力超过岩石的抗拉强度时，岩石被拉开，出现裂纹，当剪应力超过岩石抗剪强度时，该点岩石被错开，出现剪切裂纹源，岩石体积膨胀，在此过程中微裂纹扩展，出现相邻裂纹聚扰现象，如图2(b)所示；随后，裂纹扩展至自由表面，沿裂纹方向产生断裂裂纹，形成切屑，完成一次岩石的破碎过程，如图 2(c)~(d)所示。随着刀具的继续前进，将开始产生新的裂纹源，对新的岩块进行切削。

图2 刀具切削岩石裂纹形成过程Fig.2 Crack forming processes of cutter cutting rock

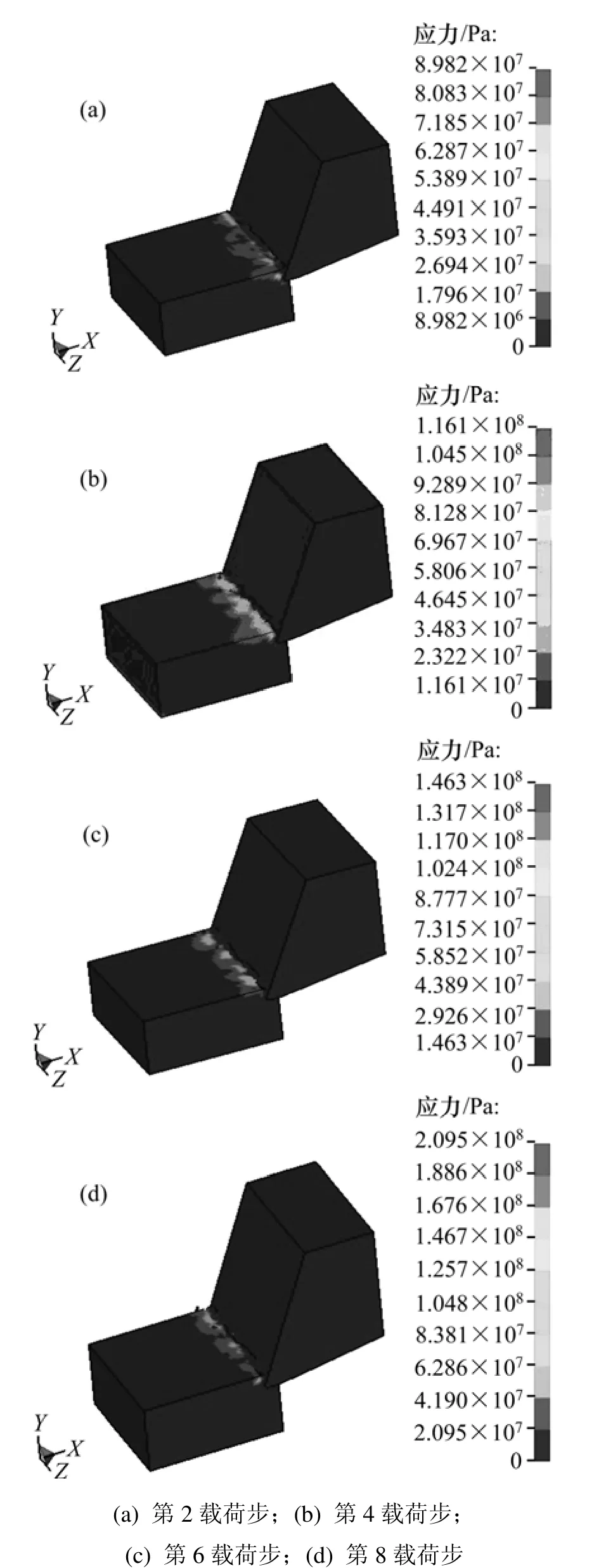
图3 各载荷步的等效应力图Fig.3 Von-mises of different load steps

2.2 三维仿真分析结果

图3 所示为不同载荷步刀具切削岩石的等效应力云图。从图3可看出：随着刀具的切入，岩石受到的挤压力逐渐增大；当岩石受到的应力超过岩石的失效强度时，岩石发生塑性变形，切屑从刀刃接触处发生断裂，岩石发生分离，单元失效删除，形成了被切削和未切削2部分材料；岩石受到刀具的挤压力很小，随着切削的不断进行，岩石受到的挤压力又逐渐增大，所以，在整个切削岩石过程中，岩石受到一个先增大后减小的循环压力作用。

图4所示为不同方向切削作用力随时间的变化关系。从图4可以得到：在刀具开始接触岩石时，刀具的受力最大且有较大波动。这是因为动态切削时，具有一定的刀具加载速度；在刚与岩石接触时，形成了较大的冲击，造成载荷突然升高；当进入稳定切削过程之后，在切削初期，由于岩石表面弹性变形，切削力迅速增加；进入压实、破环区之后，由于周围未损坏的岩石约束，岩石破碎，切削力继续增加，岩石破碎的运动趋势推动周围岩石向前运动；当边裂纹延伸至周围未损坏岩石的自由表面时，刀具前方的岩石与底部岩石发生分离，并形成切屑，完成1次岩石的跃进式断裂破碎。随着刀具的继续切入岩石，上面过程反复进行。从图4得到：X方向的切削作用力(即水平力)平均值约为3.65 kN，Y方向的切削作用力(即垂直力)平均值约为1.72 kN。

图4 不同方向切削作用力随时间变化的曲线Fig.4 Changing curve of cutting forces of different direction

图5 实验测得切削力与切削时间的关系Fig.5 Relationship between experimental cutting forces and time

2.3 试验验证

为了验证仿真结果，在室内岩石切削破碎试验台上进行试验验证。试验台主要由水平液压加载装置、垂直液压加载装置、刀具安装装置、控制台等组成。采用应变测试的方法测量应变，计算盾构掘进机切刀切削岩土时刀具受到的荷载。

通过试验得到切削力与时间的关系，如图5所示。从图5可见：X方向的平均切削作用力(即水平力)约为4.01 kN，Y方向的平均切削作用力(即垂直力)约为1.94 kN。其中X方向切削力的仿真计算值比实验测量值大8.9%，Y方向切削力的仿真计算值比实验测量值大9.6%，可见模拟得到的切削力和实验值基本一致(存在较小误差的原因主要为：有限元模型中的刀具为绝对锋利的刚体，而实际切削过程中，随着切削的进行，刀具会有不同程度的磨损；此外，在实际切削过程中，试验台产生振动，刀具由于“动平衡效应”也会产生振动，而模拟完全是在一种理想的情况下进行的)，从而验证了有限元分析方法的正确性，这也为采用该方法进行刀具工作参数和几何参数的优化提供了一种比较合适的途径。

3 切削特性分析

考虑实际切削过程中刀具几何参数和切削参数，仿真研究切削力的变化，寻找切削参数和刀具几何参数对切削的影响规律，以便为实现对物理现象的控制和切削参数的优化选择奠定基础。由于后角对整个切削过程力学方面的影响远小于前角的影响，故在进行参数优化时采用固定后角改变前角的方案。又因为在盾构机工作过程中，切削力随切削速度的变化呈波动状态，在常用的切削速度范围内，切削速度对裂纹的扩展、岩石的强度没有明显的影响，从总体上看，切削速度对切削力的影响不大，因此，不分析其对切削力的影响。在本文中，采用有限元仿真的方法，通过分别改变单一因素刀具前角、切削深度以及刀具倒圆角，得到各因素的变化对切削力的影响，并进行相应分析。

图6 刀具前角对切削力的影响Fig.6 Effect of rack angle on cutting force

3.1 刀具前角与切削力的关系

盾构刀具切削软岩时，主要承受冲击载荷的作用，前角一般在 10°~20°之间变化，本文在分析中，分别取前角为 10°，13°，15°，18°和 20°，分析其对切削力的影响，见图6。从图6可以看到：前角变化对切削过程中的切削力有很大的影响；在切削过程中，切削力随着前角的增大而减小。这是因为当前角增大时，剪切角也随着增大，切屑变形减小，沿前刀面的摩擦力也较小，因此，切削力降低。反过来，前角过小，刀具很牢固，但所受到的推挤作用很大，切割岩土的作用减弱，增加了切割阻力，不利于切削，导致切削力增加。

3.2 切削深度与切削力的关系

在现场施工中，当切削软岩地层时，一般采用的贯入度为10 mm，因此，本文选取的切削深度为8，9，10，11和12 mm，分析其对切削力的影响，见图7。从图7可以看出：切削力与切削深度的关系曲线并非呈完全的线性关系，但总体趋势是在其他切削参数不变的情况下，切削力随切削深度的增大而递增；但当切削深度增大到一定值之后，曲线斜率变大，切削深度对切削力的影响相当显著。因此，在实际施工过程中，必须严格控制刀具的切深，以免刀具由于受力过大，出现崩裂而失效，影响施工效率。

图7 切削深度对切削力的影响Fig.7 Effect of cutting depth on cutting force

3.3 刀具倒圆角与切削力的关系

改变刀具的倒圆角，分别取倒圆角半径为0，0.5，1.0和1.5 mm，研究倒圆角与切削力的关系，如表1所示。从表1可见：切削力随着倒圆角的增大而增大。这是因为：倒圆角增大能够增大切削刃强度，减小刀具崩刃与破损。因此，当刀具为较大前角时，加工出一定的倒圆角，这样，既保证刀具的切削力太大，又可以提高刀具切削部分的强度，尽可能延长刀具的使用寿命。

表1 刀具倒圆角半径与切削力Table1 Radius of cutter fillet and cutting force

4 结论

(1) 岩石的破碎过程和切屑的形成过程是由拉伸裂纹和剪切裂纹延伸而成的。

(2) 采用有限元方法有效地实现了盾构刀具切削软岩的全过程模拟，通过实验验证了该方法的可行性，为盾构刀具几何参数和工作参数的优化提供一条可靠途径。

(3) 在仅考虑单一切削变化的情况下，切削力随刀具前角的增大而减小，随切削深度的增大而增大；此外，倒圆角的变化也对切削力产生较大的影响。

(4) 所得到的切削参数与切削力的变化关系可以用于指导刀具几何参数以及切削用量的合理选择，最终实现刀具破岩的优化设计。

[1] 张绍和, 鲁凡. 金刚石钻头参数设计规律[J]. 中南大学学报:自然科学版, 2004, 35(2): 195-200.

ZHANG Shao-he, LU Fan. Designing method about parameters of impregnated diamond Bit[J]. Journal of Central South University: Science and Technology, 2004, 35(2): 195-200.

[2] 练章华, 林铁军, 孟英峰, 等. 气体钻井破岩过程动态仿真模拟[J]. 天然气工业, 2008, 28(6): 88-89.

LIAN Zhang-hua, LIN Tie-jun, MENG Ying-feng, et al.Dynamic simulation of rock-breaking process during gas drilling[J]. Natural Gas Industry, 2008, 28(6): 88-89.

[3] 苏利军, 孙金山, 卢文波. 基于颗粒流模型的 TBM 滚刀破岩过程数值模拟研究[J]. 岩土力学, 2009, 30(9): 2823-2829.

SU Li-jun, SUN Jin-shan, LU Wen-bo. Research on numerical simulation of rock fragmentation by TBM cutters using particle flow method[J]. Rock and Soil Mechanics, 2009, 30(9):2823-2829.

[4] Korinets A R. DIANA modeling of a rolling disc cutter and rock indentation[J]. Rock Mechanics, 1996, 36(8): 647-652.

[5] Carpinteri A, Chiaia B, Invernizzi S. Numerical analysis of indentation fracture in quasi-brittle materials[J]. Engineering Fracture Mechanics, 2004, 7(4/6): 567-577.

[6] Tan X C, Kou S Q, Lindqvist P A. Simulation of rock fragmentation by indenters using DDM and fracture mechanics[J]. Rock Mechanics, 1996, 36(8): 685.

[7] Kou S Q, Lindqvist P A, Tang C A, et al. Numerical simulation of the cutting of inhomogeneous rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(5): 711-717.

[8] Liu H Y, Kou S Q, Lindqvist P A, et al. Numerical simulation of the rock fragmentation process induced by indenters[J].International Journal of Rock Mechanics and Mining Sciences,2002, 39(4): 491-505.

[9] Gong Q M, Jiao Y Y, Zhao J. Numerical modeling of the effects of joint orientation on rock fragmentation by TBM cutters[J].Tunnelling and Underground Space Technology, 2005, 20(2):183-191.

[10] 陈文琳, 刘宁, 李伟, 等. 金属切削过程的三维数值模拟[J].农业机械学报, 2008, 39(1): 151-155.

CHEN Wen-lin, LIU Ning, LI Wei, et al. 3-D numerical simulation on metal cutting process[J]. Journal of Agricultural Machinery, 2008, 39(1): 151-155.

[11] 潘勇智, 艾兴, 唐志涛, 等. 基于切削力预测模型的刀具几何参数和切削参数优化[J]. 中国机械工程, 2008, 19(4): 428-431.

PAN Yong-zhi, AI Xing, TANG Zhi-tao, et al. Optimization of tool geometry and cutting parameters based on a predictive model of cutting force[J]. China Construction Machinery, 2008,19(4): 428-431.

[12] 谢峰, 刘正士, 赵吉文. 纳米TiN改性的TiC基金属陶瓷刀具有限元分析[J]. 农业机械学报, 2004, 35(4): 167-170.

XIE Feng, LIU Zheng-shi, ZHAO Ji-wen. FEM analysis of TiC-cermet cutter modified by Nano TiN[J]. Journal of Agricultural Machinery, 2004, 35(4): 167-170.

[13] Ma G W, An X M. Modelling of dynamic behavior of concrete materials under blast loading[J]. Solids and Structures, 2004,41(2): 131-143.

[14] ZHANG Yong-qiang, LU Yong, HAO Hong. Analysis of fragment size and ejection velocity at high strain rate[J].Mechanical Sciences, 2004, 46(1): 27-34.