甚低频在多模干涉区的场强起伏标准偏差估计

张世田 陈恩平 王元新 潘威炎 张红旗

(中国电波传播研究所，山东 青岛 266071)

1. 引 言

甚低频(VLF)波是指频率范围为3～30 kHz的电磁波，其工作波长为100～10 km，地面与电离层对此频段的电磁波具有良好的反射特性，电波在地面与电离层之间来回反射导引传播，从而构成地—电离层波导[1-2]。由于VLF波传播损耗小、信号稳定、且能够渗透一定深度的海水从而在海军通信与导航中有重要应用。

VLF在地-电离层波导中有多个传播波模，每个传播波型都有各自的传播相速、衰减率、激励因子等，接收点的信号场强是各个传播波型叠加的结果。在各个传播波模中，TM0波模的衰减率最低，称作为基模。在几千千米以外，高阶波模已衰减至不起作用，称作单模区。在中近区因为多个波模同时存在，各个波模的传播相位不尽一致，故出现“干涉”现象，称之谓“多模干涉区”。

由于电离层的状态不是固定不变的，对于固定接收点而言，信号的幅度与相位亦是有变化的，除了随季节、昼夜的规则变化外，还有随机的不规则变化。传播相位随机起伏标准偏差对于VLF导航系统而言，是影响导航定位精度的重要参数，而信号场强起伏的标准偏差则是估计VLF通信可靠度的重要参数。

美国学者Watt根据10～20 kHz范围内的各种测试结果, 在文献[3]给出大距离条件下(单模区)传播相位起伏标准偏差的一个经验公式，同时给出了相应场强起伏偏差的估计。但此二经验公式仅适用于单模区，对于多模区特别是场强极小点附近不适用。文献[4]给出了多模区VLF传播相位起伏标准偏差的估计公式，此公式在单模区自动地转化为美国学者给出的公式，在多模区与我国的实测结果吻合的相当好。但迄今为止，多模区VLF场强起伏标准偏差的估计尚未有较好的方法。本文将对此深入分析研究。

2. 多模干涉区内的场强和传播相位的空间变化

依据VLF波导的传播理论[5]对于地基的发射天线而言，它产生的VLF电场垂直分量可表示为

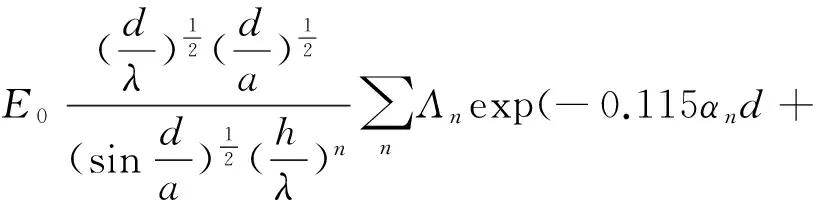
(1)

式中：

(2)

p是辐射功率以kW计；d是收发点之间大圆距离以km计；a是地球半径6370 km；h是电离层高度；λ是自由空间波长；Λn,αn,υn分别为第n阶模的激励因子、哀减率和相速。若记第n阶模的相对幅度和相位分别为Fn和φn，则有

Fn=|Λn|exp(-0.115αnd)

(3)

(4)

当考虑到沿传播路径上，由于传播条件的变化，各阶模的参数可能不均匀，则

(5)

(6)

此时总的电场可表示为

(7)

总场的幅度可表示为

(8)

式中M为幅度干涉因子，表示高阶模对总场幅度的影响。

(9)

根据文献[6]场强随距离变化的表达式，文献[7]提供的地面电磁参数可计算白天沿传播路径上场强的幅度，并与文献[8]的实测数据进行了比较，如图1所示。

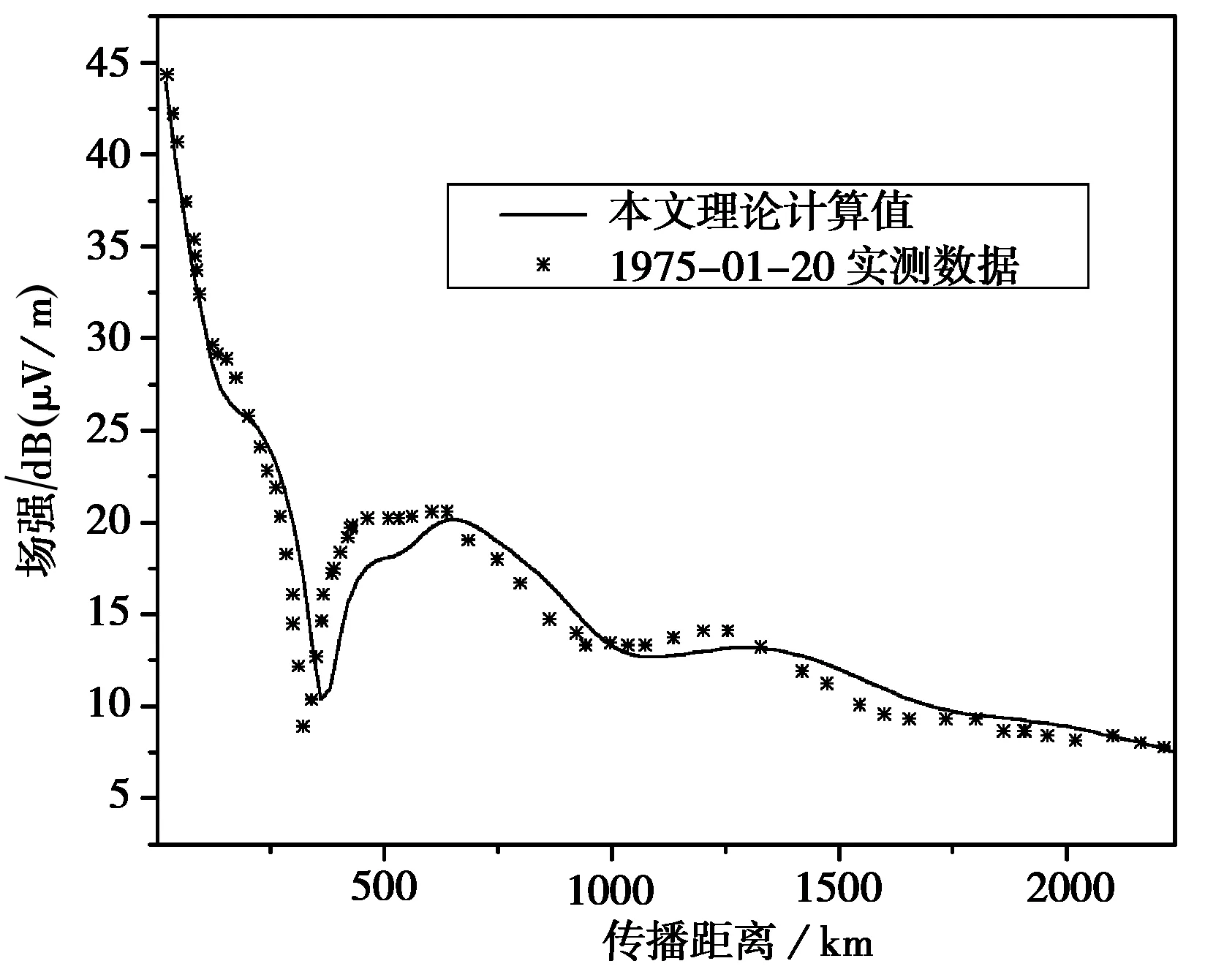
图1 场强随传播距离的变化(大同至海口)

由图1可见理论计算值与实测值能够较好的吻合，这也说明了传播路径上各阶模的传播参数计算值是准确的。

3. 引起信号幅度和相位随机起伏的理想化

根据文献[5]将电离层随机变换引起的VLF幅度和相位的随机变化理想化为沿传播路径的等效反射高度的随机变化所致，即认为沿传播路径上的电离层等效反射高度可以表示为

h(d,t)=h0(d)+δh(d,t)

(10)

式中：h(d，t)表示传播路径上某地在时刻t的电离层等效反射高度；h0(d)是该地点电离层反射高度的期望值； δh(d,t)是它的随机变化部分，它的期望值应为0.即

E(δh(d,t))=0

(11)

电离层等效反射高度随机起伏引起的各个模式的相位和相对幅度的随机变化可由式(3)和(4)求出，它们是

(12)

(13)

dαn/dh和dυn/dh分别代表第n阶模衰减率和相速对于电离层等效反射高度的导数，可由波导理论计算出来。从式(12)和(13)可以看出，各阶模的幅度与相位亦有相应的随机变化，它们与电离层等效反射高度随机起伏有关的随机变化量dξ成正比，其中

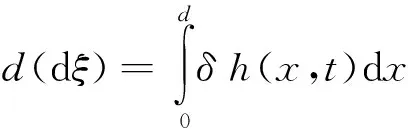
(14)

4. 信号幅度随机起伏标准偏差的估计

由式(8)可得，当沿传播路径上，电离层等效反射高度有随机起伏变化时，接收点信号幅度应有相应的随机变化，可以表示为

(15)

(16)

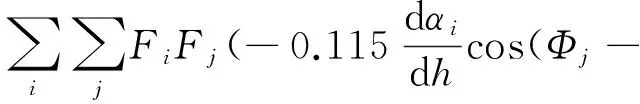
(17)

函数G(d)、M(d)等都是仅与接收点地理位置(传播距离)有关的函数，而dξ是由于电离层等效高度随机变化引起的随机变量。

假定δh(d,t)在传播路径上各点都是呈正态分布，且其标准偏差相等，则它们的积分亦是呈正态分布，且其期望值应为

(18)

方差应为

(19)

式中：

(20)

是等效高度随机起伏沿传播路径的归一化自相关函数。

若认为等效高度随机起伏的自相关函数能用指数函数描述，且相关距离为L，则

(21)

将式(21)代入式(19)可得

(22)

当d>>L，则

D(dξ)≈2LdD(δh)

(23)

(24)

由式(16)和(8)可以看出，接收点场强幅度的相对变化为

(25)

式(25)中，仅有dξ是随机变量，故接收点场强起伏标准偏差可估计为

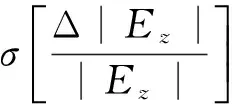
(26)

当接收点距离发射点相当远时，高阶模已衰减至不起作用，则有

M(d)≈|F1|

(27)

(28)

在此情况下，式(26)可以退化为

(29)

如果将场强起伏标准偏差以dB表示(d以千km为单位)，则应有

(30)

由文献[3]可知

(31)

式中，系数K在白天取为1，夜晚取2.4.

故式(30)可进一步表示为

(32)

式中

(33)

图2给出了白天大同到海口路径上场强标准偏差随距离的变化曲线。

图2 白天大同-海口路径上多模干涉区场强起伏标准偏差随传播距离地变化(频率12.5 kHz)

从图2可以明显看出：由于存在多模干涉，在多模干涉区场强的稳定性比较差，尤其是在距发射台600 km范围内；在多模干涉区公式(29)不适用，但是在单模干涉区式(33)计算结果与式(29)结果能够较好的吻合；我们提出的标准偏差估计公式的计算结果与文献[8]实测数据的标准偏差一致且吻合良好。对比结果表明，我们提出的多模干涉区场强起伏标准偏差公式可以更准确地反映出整个传播路径上场强的起伏变化。

5. 结 论

目前，国内对多模区VLF场强起伏标准偏差的估计方法研究较少，没有提出明确的场强起伏标准偏差的公式。国外也只是给出了单模干涉区场强起伏标准偏差估计的经验公式。而我们给出的场强起伏标准偏差估计公式，可以较好的应用于多模干涉区、单模干涉区及场强极小点附近。通过与实测数据的对比，证明此场强起伏标准偏差估计公式能够较准确地反映出电离层的随机变化对传播路径上场强的稳定性的影响。此偏差估计公式对VLF通信可靠性的研究具有重要意义。

[1] WAIT J R and SPIES K P. Characteristics of the earth-ionosphere wavequide for VLF radio wave[M]. NBS Tech note, No.300, 1964.

[2] GALEJS J. Terrestrial propagation of long electromagnetic wave[M]. NewYork: Pergamon press, 1972.

[3] WATT A D. VLF radio engineering[M]. NewYork: Pergamon press, 1967.

[4] PAN Weiyan and TIAN Yushu. Multi mode interference and phase stability of VLF wave propagation[C]//International Symposium on Radio Propagation, 1988: 40-43.

[5] 潘威炎. 长波超长波极长波传播[M]. 成都: 电子科技大学出版社, 2004.

[6] 潘威炎, 田育庶, 等. 甚低频(VLF)无线电系统场强与相位计算方法[S]. 中华人民共和国国家军用标准, 1994.

[7] CCIR report 717-1.World atlas of ground conductivities[R]. 1982.

[8] WEN F R and XIONG H. The multimode interference of vlf radiowave propagating in near-medium ranges[C]//International Symposium on Radio Propagation, 1988: 36-39.