两点源角度拖引干扰方法研究

施龙飞 李艳斌 葛 蕾 杨书玲 刘 健

(1.国防科技大学电子科学与工程学院，湖南 长沙 410073； 2.中国电子科技集团第五十四研究所，河北 石家庄 050081)

1. 引 言

随着单脉冲测角、相控阵等先进雷达技术的发展应用，现代军用雷达的抗干扰能力越来越强，雷达干扰面临着更为复杂的困难[1]。

为了摆脱雷达导引头的角度跟踪，减轻主动制导导弹对飞行平台的威胁，拖曳式诱饵等角度欺骗干扰已经广泛应用于机载雷达对抗装备中，并在数次实战中发挥了重要作用。但是这类干扰都是在近距离上、以导弹末制导雷达为对抗对象的[2]。若能够在中、远距离上对地基/舰载雷达的跟踪进行欺骗干扰，则能够大大提高突防成功率和突防飞机的战场生存能力。

2. 理论分析

2.1 两点源角度欺骗干扰

角度欺骗干扰是雷达对抗中广泛采用的干扰样式，其主要目的是使雷达角度测量跟踪系统偏离被保护平台。角度欺骗干扰的本质是使雷达接收天线口径面处的目标回波相位波前发生畸变。

两点源角度欺骗干扰是角度欺骗干扰中应用最为广泛的一种，广义的两点源干扰样式包括两类，即相干两点源干扰(包括交叉眼干扰[2]等)和非相干两点源干扰(地面反弹干扰、普通拖曳式诱饵等[3])。本文主要考虑采用相干两点源干扰的方式。

相干两点源干扰的归一化角闪烁线偏差可记为[2](归一化线偏差定义为：两源视在中心与两源中心的横向距离经两源横向尺度归一化后的值[4]，“横向”指的是在目标中心与雷达接收天线之间连线的垂直平面上的投影，如图1所示)

(1)

式中： 可将ρ·exp{jρφ}作为到达雷达天线的干扰源2与干扰源1 信号的相对系数； ρ和φρ分别为相对系数的幅度和相位。

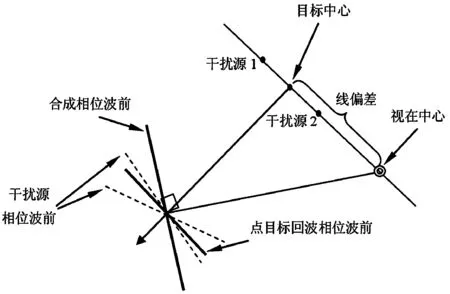
图1 角度欺骗干扰的作用机理

由式(1)可得，归一化线偏差e随相对系数幅度ρ和φρ相位的变化如图2所示，且

1) 当φρ为180度时，e(绝对值)为峰值点，当φρ接近0度或360度时，e接近于0；

2)ρ越接近于1，线偏差曲线的峰值越大，当ρ=1时，该峰值点趋于无穷大；

3) 参数ρ和1/ρ对应的线偏差曲线以e=0为轴对称分布，且ρ>1时在该轴的上方，ρ<1时在该轴的下方。

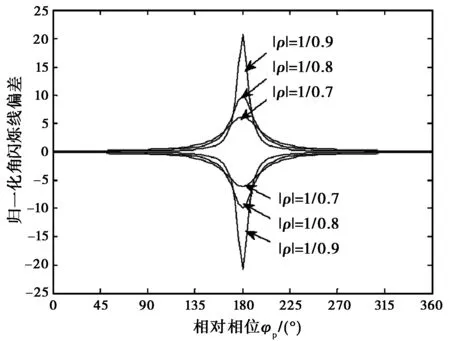
图2 线偏差随相对系数幅度和相位的变化

由上面分析，若能够对两点源的相对幅度和相对相位进行精确控制，则产生的线偏差值将非常大，从而达到非常好的干扰效果。但由于干扰源1与干扰源2到达雷达天线口面处的路径是不一样的，因此两信号相对相位φρ包括了路程差带来的相位差φρL和干扰发射源本身的相位差φρS两部分，即

φρ=φρL+φρS

(2)

由于路程差难以准确获知，φρL难以获知，因此，总相位φρ难以控制，从而两点源干扰很难达到理想的状态。 交叉眼干扰从机理上巧妙地化解了这一问题：采用转发干扰方式，干扰源1转发从干扰源2处接收到的雷达信号，而干扰源2转发从干扰源1处接收到的雷达信号，因此两干扰信号的总路程相同、不存在路程差(φρL=0)，干扰机只需对φρS进行控制，理论上能够实现非常好的角度欺骗效果。

然而，目前来看，交叉眼干扰在实际应用和工程实现上还存在着较大的困难，主要是两个方面：(1) 实际应用中，由于机载平台的位置和姿态都是快速动态变化的，从接收到发射的时间内，两干扰信号的路程差会引起φρL较大的扰动；(2) 工程实现中，由于采样、数字处理、时钟同步等原因，两干扰信号相对相位较难控制。

鉴于上述两个方面的原因，交叉眼干扰虽然理论上具有非常好的干扰效果，但受硬件系统水平的限制，目前尚未得到大范围的成功应用。

另一方面，随着空中作战平台向网络化的方向发展，利用多机编队实现合成干扰可以解决单机干扰在时间、空间、频谱上的局限性，特别是对于先进相控阵雷达组网的情况，通过多机雷达对抗系统的密切配合，可有效地消除雷达组网在对抗中的优势。

本文主要针对双机编队角度欺骗干扰，立足于两源相对相位φρ随机不可控的情况，研究对相对幅度ρ的控制规则，使角度欺骗干扰能够达到最佳的干扰效能。

2.2 两点源角度欺骗干扰参数设计

2.2.1 角度测量偏差统计特性

干扰环境下雷达角度测量偏差的统计特性是两点源角度欺骗干扰设计的基本依据，文献[2]在研究扩展目标的角闪烁问题时，提出以均方根和功率谱密度作为主要关注点，雷达设计者依据这两方面特性对角跟踪伺服带宽等进行设计。

与扩展目标角闪烁特性不同，由于两干扰源相对相位的随机变化且不相关，因此功率谱密度特性无法使用。另一方面，角偏差对相位很敏感(尤其是当ρ接近于1时，由图2)，考虑到雷达数据处理中会首先进行剔野再进行角度滤波，因此，本文提出以剔野后的概率密度分布特性作为角度测量偏差的主要特性。

利用式(1)，通过蒙特卡洛仿真并对结果进行统计分析，得到了两点源干扰造成的角度测量偏差概率密度分布曲线，图3是不同幅度比ρ下概率密度曲线(雷达与干扰源中心距离为60 km，两干扰源横向距离1 km，且对于偏差超过2度的测量值作为野值进行剔除)。由图3可以看出：

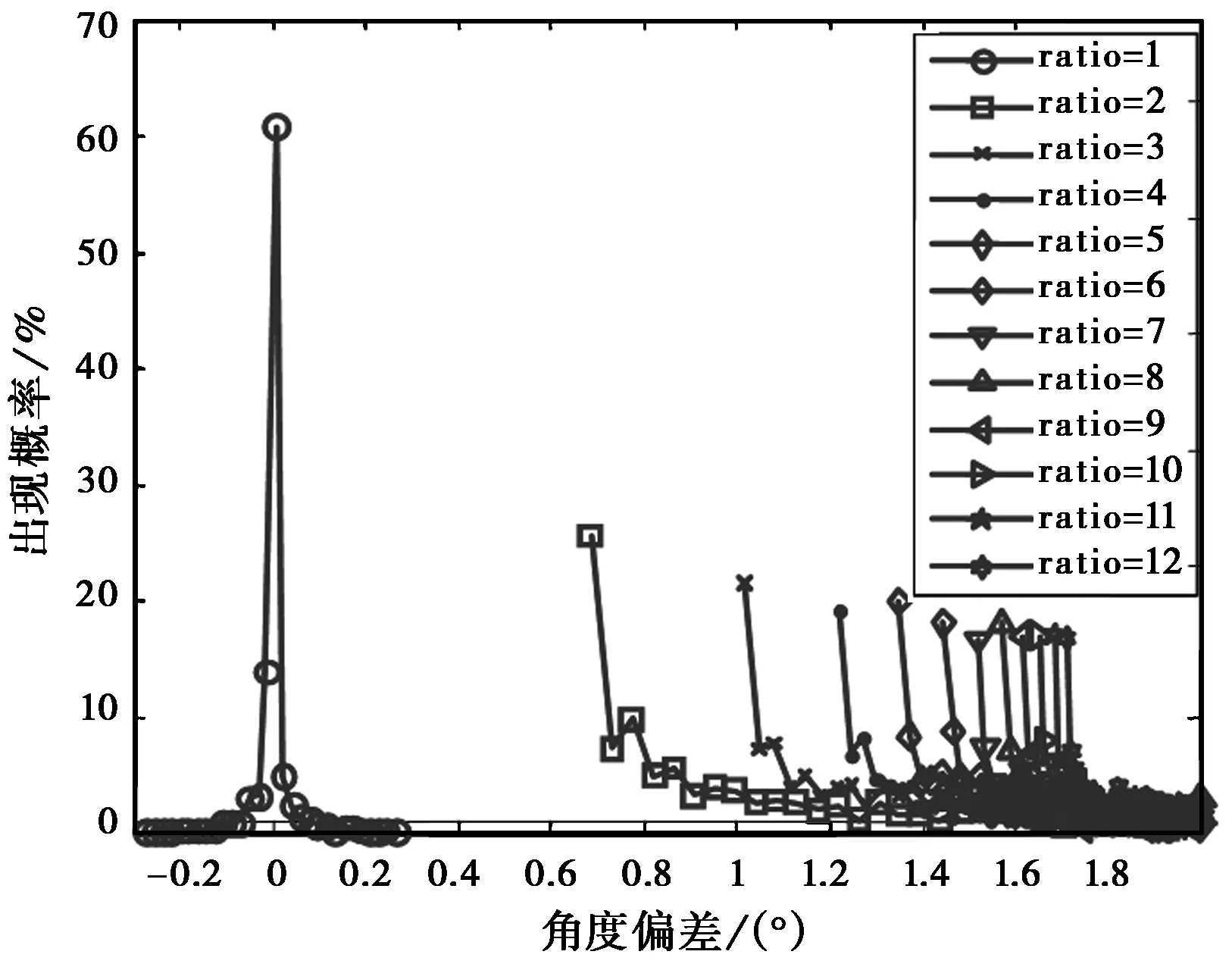
图3 不同幅度比下测量偏差概率密度分布曲线

1) 不同幅度比情况下，其角度偏差以较大概率聚集于不同区域；

2) 幅度比越大，角度偏差聚集中心(均值)逐渐增大。

图4是角度偏差均值及其变化斜率，可见：

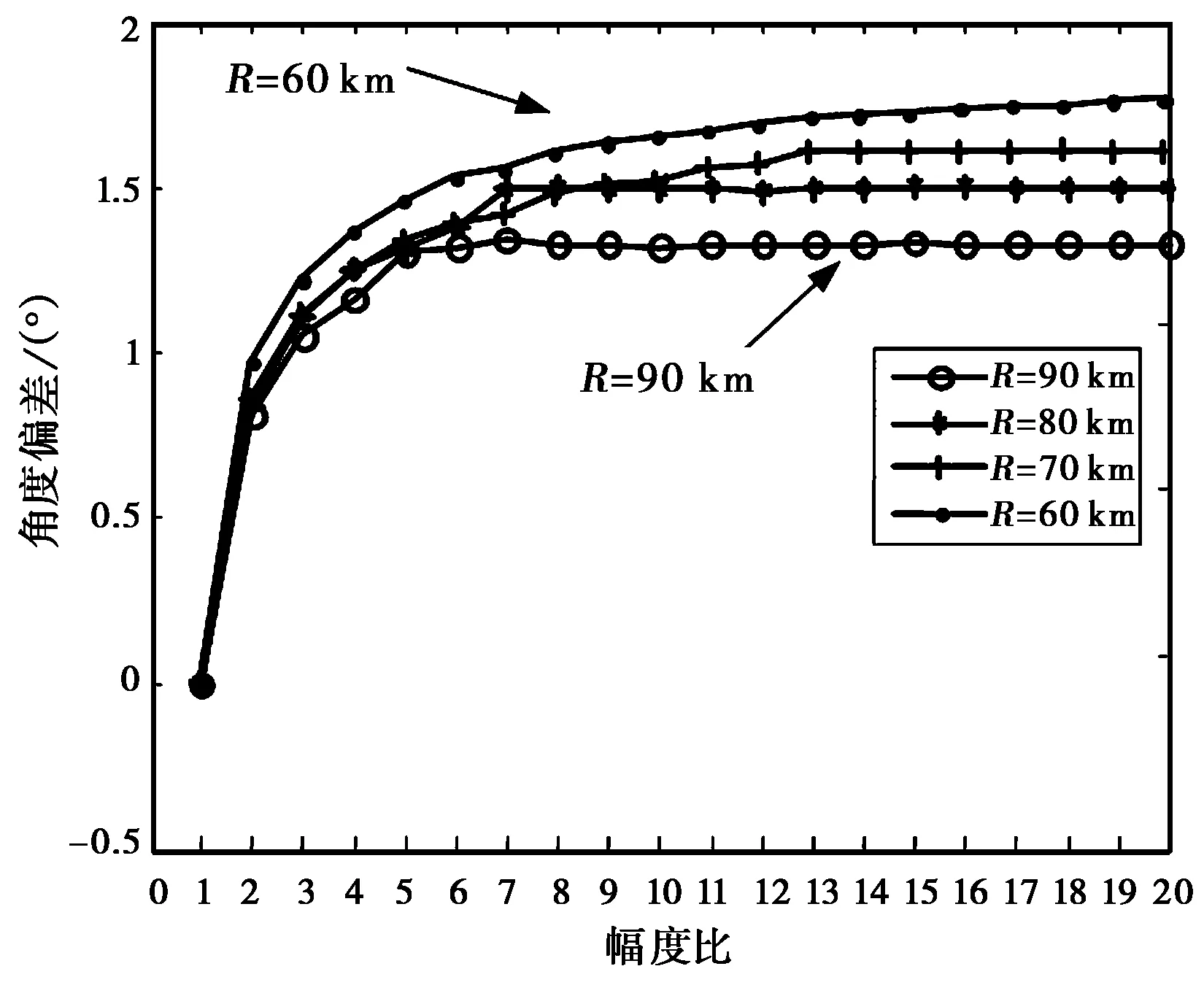
图4 角度偏差均值

1) 雷达/干扰距离越近，角度偏差均值越大；

2) 随着幅度比ρ的增大，偏差均值呈增大趋势，但趋势变缓；

3) 由图4可知，偏差均值的变化斜率随着幅度比增大而迅速下降，当ρ超过某些值之后，斜率接近于0；

2.2.2 雷达角度跟踪滤波特性分析

雷达通过对目标进行角度测量和平滑滤波实现稳定的角度跟踪。对于所有的跟踪滤波算法，一方面要适应测量误差的起伏以使跟踪尽量稳定，另一方面也要适应目标运动状态的变化，这两方面的要求使得滤波算法在参数设计上只能在两者之间进行权衡。

以角度跟踪为例，雷达跟踪滤波算法可归结为下面三个核心步骤：

1) 状态预测

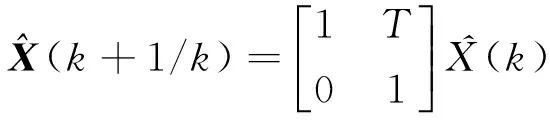
(3)

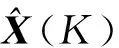
2) 新息计算

v(k+1)=Z(k+1)-

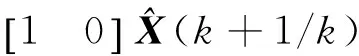
(4)

式中：Z(k+1)为角度测量值； [1 0]为观测矩阵；v(k+1)称为第k+1次的新息。

3) 状态更新

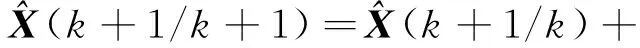
K(k+1)v(k+1)

(5)

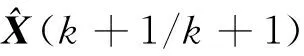
上述三个步骤分别具有不同的作用：

● 状态预测的主要用途是为雷达跟踪波束(或天线伺服)提供指向导引；

● 新息V(·)表征了目标运动状态的变化量；

●增益K(·)是滤波器对目标运动状态变化的适应度，K(·)越大表示适应能力越强，K(·)越小表示适应能力越弱，但同时其适应测量误差起伏的能力则越强。

2.2.3 角度拖引干扰设计

2.2.3.1 干扰样式设计

根据上述分析，本文提出一种新型角度欺骗干扰方式——“角度拖引干扰”,通过有规律地改变两干扰源幅度比，使雷达角度跟踪滤波器稳定地朝某一方向偏离，且偏离角度呈增大趋势，当偏离角度超过某个门限后，关闭干扰源并迫使雷达丢失目标。

在这种方式中，促使雷达丢失目标有两个方面的原因：一方面，雷达天线波束指向被引导到偏离目标的方向，目标回波接收功率大大降低；另一方面，由于干扰功率比目标回波功率大，雷达自动增益控制(AGC)被调整到低增益的状态，因此关闭干扰源后目标更难以被检测到。

2.2.3.2 干扰效能评估标准

角度欺骗干扰的目的是通过对雷达角度测量/跟踪系统进行干扰，使其跟踪到错误的角度上，并不断重复“捕获——跟踪——丢失——重新捕获”的过程。

距离波门拖引干扰效能的评估中[5]，通常以“拖引时间”和“失锁时间”作为评价指标：拖引时间是指从干扰施放到成功迫使雷达丢失目标所需要的时间；失锁时间指的是雷达从丢失目标到重新捕获并建立跟踪所花的时间。

显然，拖引时间越短、失锁时间越长，则干扰效果越好。拖引时间决定于拖引速度，而决定失锁时间的包括雷达本身的搜索性能和拖引程度。本文中，由于主要采用两点源幅度比控制的实现方法，不能够达到很大的角度偏差(如图3)，而对于具有失跟处理能力的先进相控阵雷达(雷达丢失目标后，会在其邻近区域进行快速补充搜索，该区域一般包括2～3度的区域，很可能会迅速重新捕获目标)，失锁时间很可能较短。

综合上面的分析，本文将拖引时间作为角度欺骗干扰的主要评估指标。

2.2.3.3 干扰参数设计

针对跟踪滤波器的特性，并利用角度测量偏差的统计特性进行干扰参数的设计。

雷达跟踪滤波过程中，新息V(k+1)通过增益K(·)对第k+1次的滤波输出值产生影响(式 (5))，并进而决定了下一时刻的预测值。那么，为了使雷达能够稳定地偏向某个方向，要求角度预测值和角度滤波值均稳定地向该方向偏离，因此，要求从统计上新息V(k+1)≥0，式 (4)中：

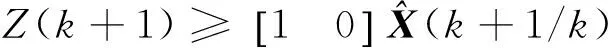
(6)

即角度测量值应大于或等于角度预测值，那么，对应于角度拖引干扰，就是匀速拖引和加速拖引两种情况，本文讨论匀速拖引和匀加速拖引两种拖引方式。

(7)

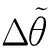
(8)

故

(9)

匀加速拖引干扰的拖引时间为

(10)

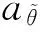
3. 实验结果分析

3.1 角度欺骗干扰对抗仿真数学建模

本文研究针对跟踪雷达的角度拖引干扰，为验证其效能，首先需要对对抗双方进行数学建模。

雷达部分的模型主要包括：天线方向图模型(方位向两阵元)、目标回波模型、匹配接收模型、检测模型、距离测量模型、单脉冲测角模型(和差波束法)、角度跟踪模型等。干扰部分的模型包括：空间几何关系模型(如图5所示)、干扰信号模型。图中，L为两干扰源之间的距离，L1为雷达天线两阵元之间的距离，R为目标中心(两干扰源连线中心)距雷达的距离。

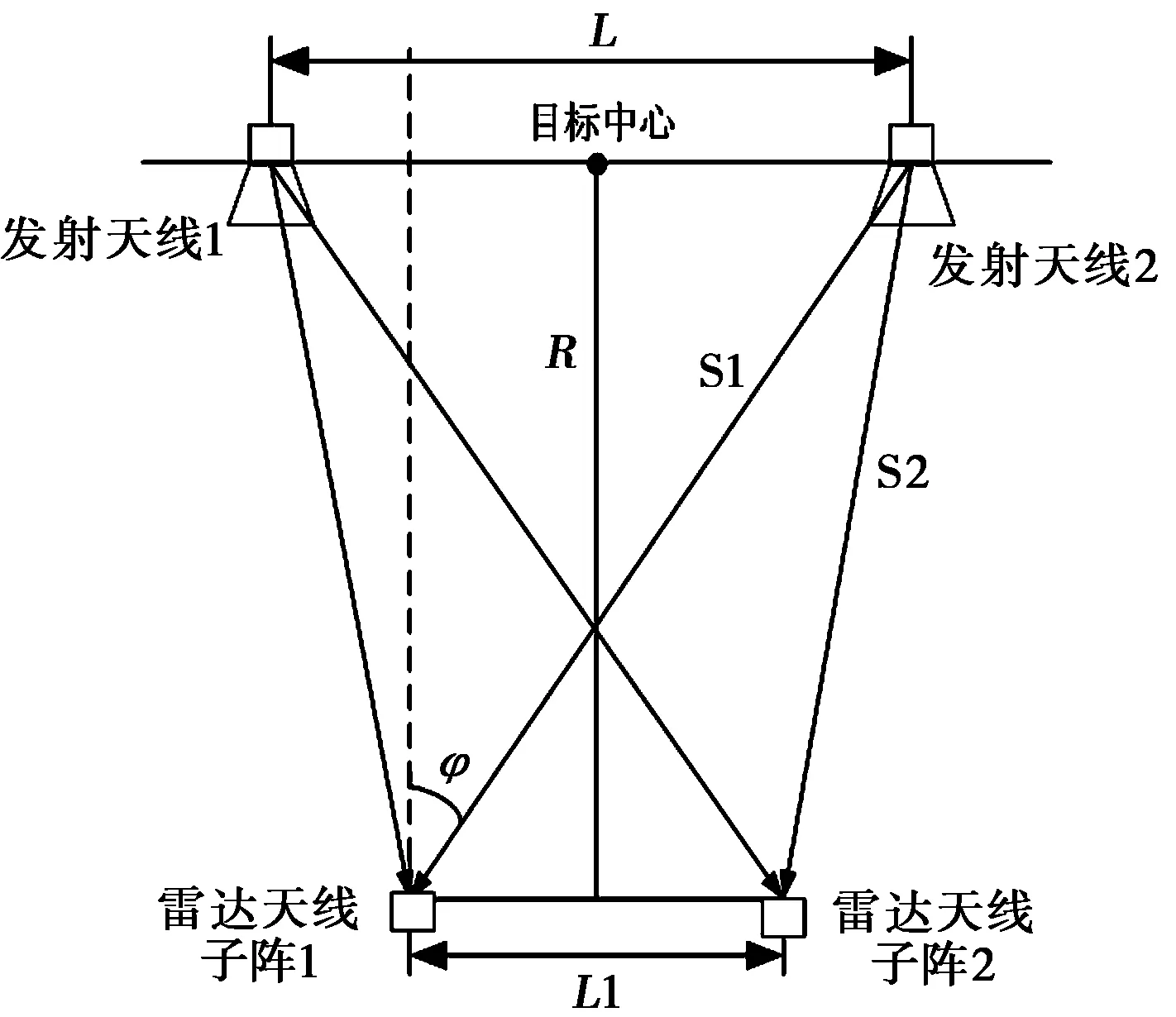
图5 两点源角度干扰示意图

本文仿真中，设定目标中心以0度方位由远及近地沿径向飞向雷达，雷达天线初始指向为0度，采用和差波束法进行角度测量，采用α-β滤波进行角度跟踪。角度欺骗干扰由一对转发式假目标组成，两假目标信号时延相同，且与真目标回波距离(时延)控制在一个距离分辨单元之内，真目标回波经匹配接收后的信噪比设为30 dB.

3.2 对常增益跟踪滤波器的角度欺骗干扰性能

以α-β滤波器为例，分别针对常增益α-β滤波和变增益α-β滤波两种情况检验匀速拖引干扰和匀加速拖引干扰的性能。

3.2.1 匀速角度拖引干扰性能仿真与分析

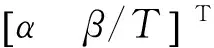
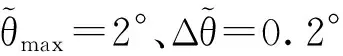
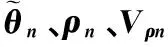
表1 匀速拖引情况下各节点的

按照上述参数进行角度拖引干扰，图6是一次完整的角度拖引过程中的雷达角度测量/跟踪结果。

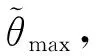
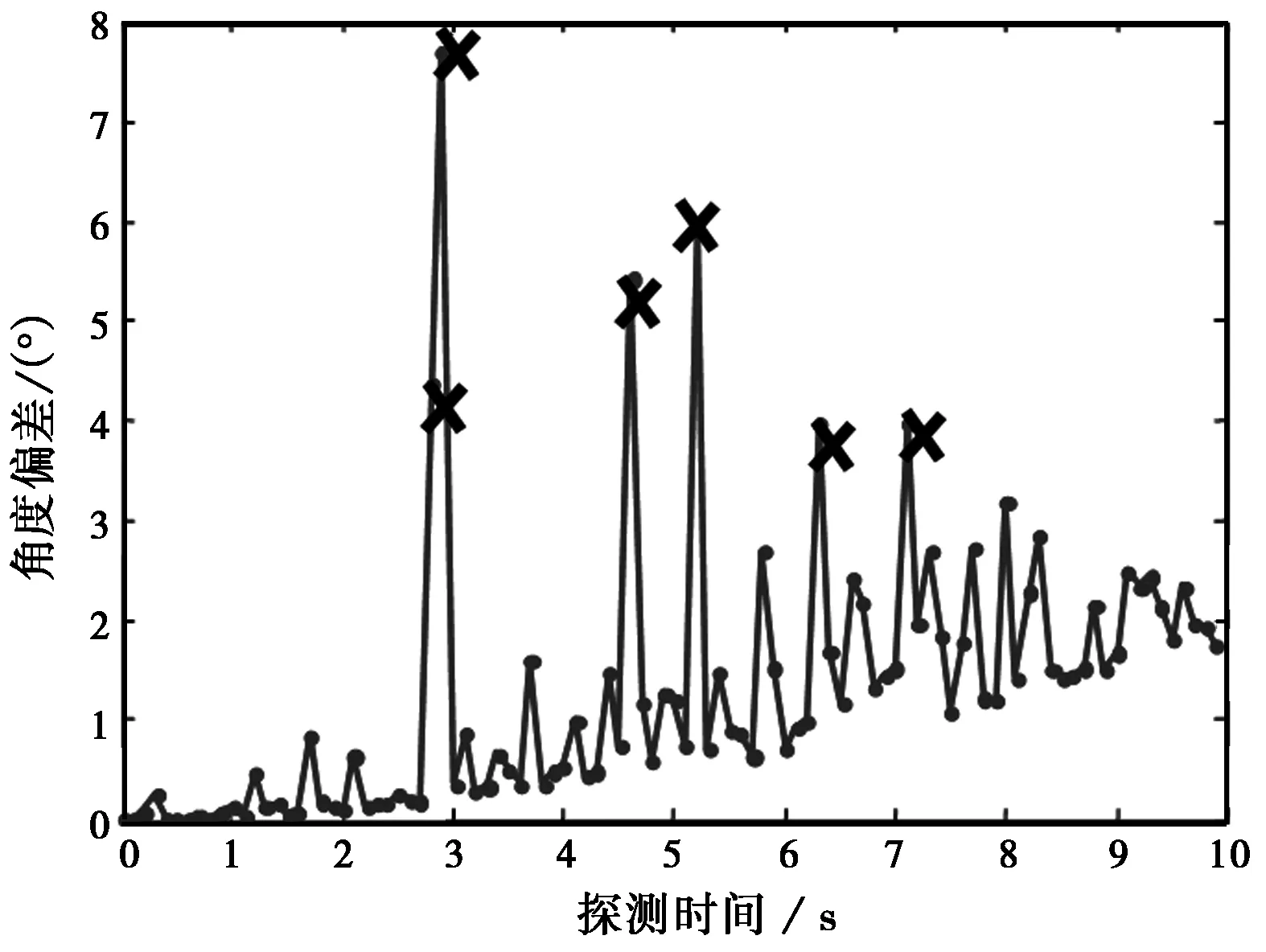
(a) 雷达角度测量值(“X”表示被剔除的野值点)

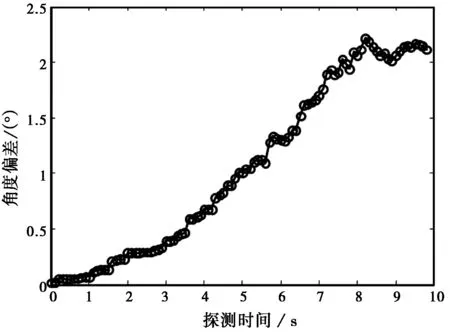
(b) 雷达角度跟踪滤波值图6 匀速拖引干扰下雷达角度测量/跟踪输出

3.2.2 匀加速角度拖引干扰性能仿真与分析

设雷达采用变增益滤波器α-β滤波器，其增益递推衰减[6]，且

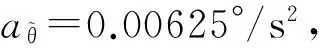
在10个节点上，对应的幅度比及其加速度速度分别如下表2所示。

表2 匀加速拖引情况下各节点的

从表2可以看出，加速度在后期迅速增大，这是因为当超过一定范围后其带来的角度偏差迅速下降(如图4示)。

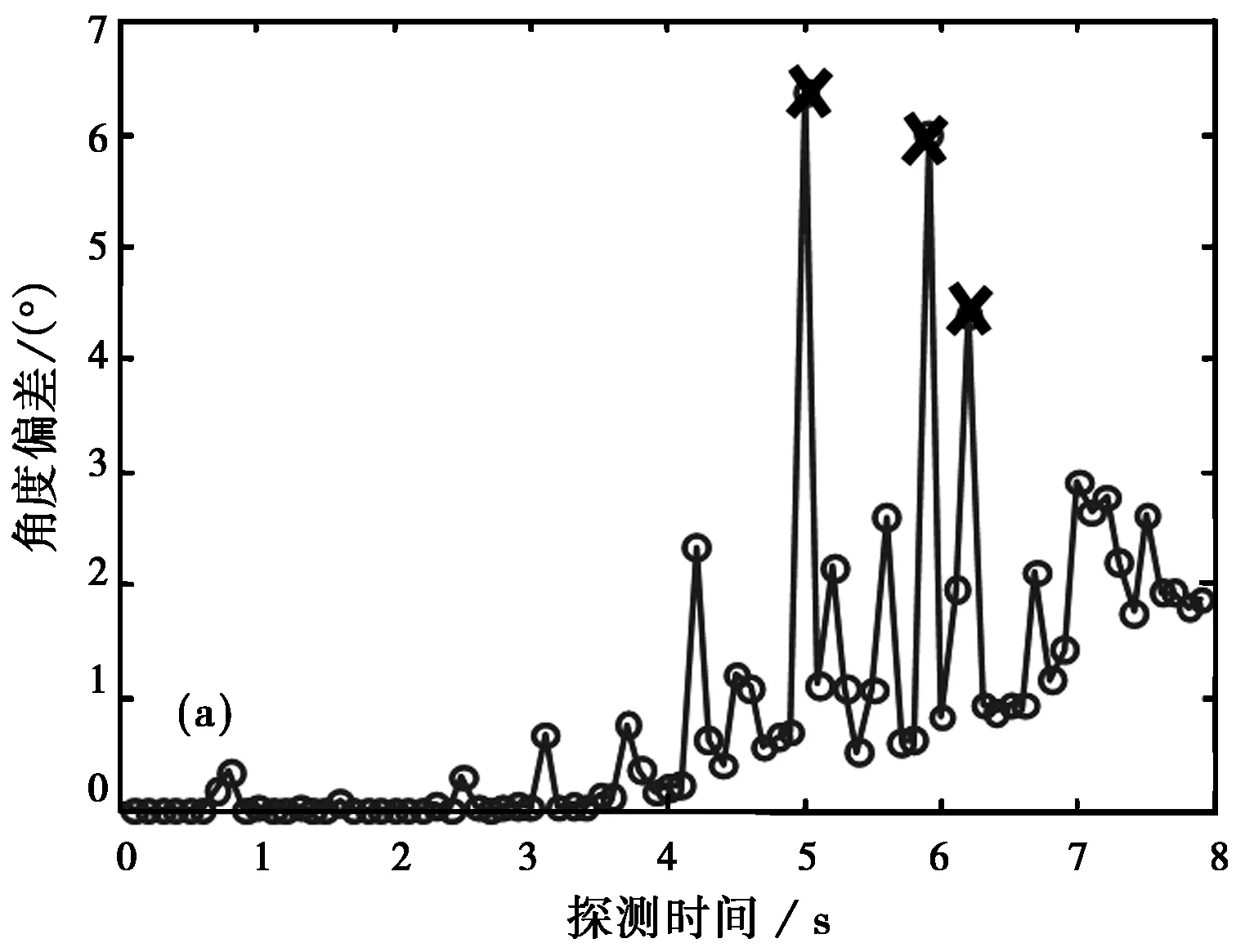
(a) 雷达角度测量值(X表示被剔除的野值点)

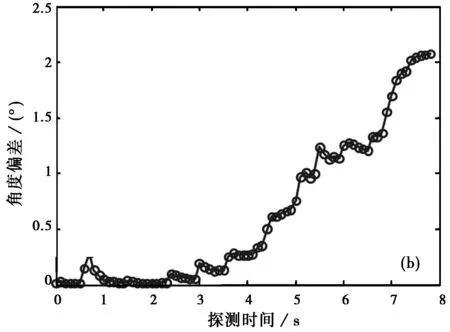
(b) 雷达角度跟踪滤波输出图7 匀加速拖引干扰下雷达角度测量/跟踪输出

限于篇幅，本文未列出所有情况下的角度跟踪输出结果。实际上，在正常的雷达参数情况下，匀速拖引干扰和匀加速拖引干扰都具有与理论预期近似的拖引干扰效果。

4. 结 论

本文提出了一种新型角度欺骗干扰样式——角度拖引干扰。该干扰立足于相位差随机不可控情况下(如双机编队)的两点源角度欺骗干扰，通过对两点源相对幅度的设计，实现了对雷达稳定的拖引欺骗，且拖引时间较短，能够对雷达精跟、锁定以至于制导形成有效干扰。

文章通过对两点源背景下雷达测角偏差统计特性的研究，并依据雷达角度跟踪滤波器的工作机理，分别提出了匀速角度拖引和匀加速角度拖引干扰，并对其参数进行了设计。

本文给出的分析和仿真都是以双机编队两点源干扰为例的，但对于相位控制精度无法达到要求的交叉眼干扰，也可以参照采用该种方法。同时，本文的研究思路和研究成果是多干扰源情况下的角度拖引干扰研究的基础，这也是我们下一步的研究目标。

[1] SKOLNIK M I. 雷达手册[M]. 北京: 电子工业出版社, 2003:7.5-716.

SKOLNIK M I. Radar Handbook[M]. Beijing: Publishing House of Electronics Industry, 2003: 715-716. (in Chinese)

[2] 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2006: 157-165.

HUANG Peikang, YIN Hongcheng, XU Xiaojian. Radar Target Characteristcis[M]. Beijing: Publishing House of Electronics Industry, 2006: 157-165. (in Chinese)

[3] 侯民胜, 朱 莹, 樊晓明. 单脉冲雷达的闪烁干扰技术研究[J]. 现代电子技术, 2009, 302(15): 1-3.

HOU Minsheng, ZHU Ying, FAN Xiaoming. Study on blinking jamming technique for monopulse radar[J]. Modern Electronics Technique, 2009, 302(15): 1-3. (in Chinese)

[4] 施龙飞, 王雪松, 肖顺平. 低空镜像角闪烁干扰的极化抑制[J]. 电波科学学报, 2008, 23(6): 1038-1044.

SHI Longfei, WANG Xuesong, XIAO Shunping. Depressing of angle glint of low altitude enantiomorphous target by polarization diversity[J]. Chinese Journal of Radio Science, 2008, 23(6): 1038-1044. (in Chinese)

[5] 解 凯, 陈永光, 汪连栋, 等. 距离波门拖引方案的分析建模与评估[J]. 系统工程与电子技术, 2006, 28(8): 1158-1163.

XIE Kai, CHEN Yongguang, WANG Liandong. Analysis, modeling & evaluation of range gate pull off design[J]. Systems Engineering and Electronics, 2006, 28(8): 1158-1163. (in Chinese)

[6] 王国玉, 汪连栋, 王国良, 等. 雷达电子战系统数学仿真与评估[M]. 北京: 国防工业出版社, 2004: 141-155.

WANG Guoyu, WANG Liandong, WANG Guoliang. Simulation and Evolution of Radar and EW System[M]. Beijing: Defense Industry Press, 2004: 141-155. (in Chinese)

[7] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991: 134-144.

ZHOU Hongren, JING Zhongliang, WANG Peide. Tracking of Maneuvering Targets[M]. Beijing:Defense Industry Press, 1991: 134-144. (in Chinese)