基于微多普勒特征的空间锥体目标识别
关永胜 左群声 刘宏伟
(1.西安电子科技大学雷达信号处理国防科技重点实验室,陕西 西安 710071; 2.西安电子科技大学通信工程学院,陕西 西安 710071; 3.中国电子科技集团公司,北京 100846)
1.引 言
空间锥体目标识别任务是从大量的诱饵和空间碎片等构成的威胁云团中识别出目标。目前的研究热点主要围绕着基于雷达散射截面(RCS)、一维距离像或二维逆合成孔径雷达像(ISAR像)展开特征提取与识别方法的研究。
最近研究表明,微动(例如目标部件或结构的振动旋动)可以对雷达回波产生额外的频率调制,为了区别于目标的多普勒频率,此频率被称为微多普勒[1]。它提供了目标识别的新方法,在目标分类与识别领域显示了巨大的潜力。文献[1]-[4]对不同微动形式产生微多普勒效应的分析,深化了人们对机动部件多普勒谱调制现象的认识,使得从目标回波的多普勒信息中提取有利于分类和识别的特征有了新途径。
文献[5]-[7]指出空间锥体目标在太空飞行过程中存在不同的微动,目标特有的微动为进动而诱饵的微动为摆动自旋。依据目标微动特性的差异,可望为目标识别难题提供新的解决手段。美国2004年资助了一项创新研究,使得AN/SPY-1相控阵S波段雷达能够利用微多普勒特征识别威胁目标[8]。文献[9]研究了空间锥体目标的进动模型并采用时频分析方法抽取微多普勒特征。文献[10]通过目标运动分辨(TMR)技术提取目标运动参数。文献[11]引入微进动和微RCS的概念,使用进动锥体目标的微RCS序列估计惯量比,以惯量比为特征,提出了识别方法。
本文主要探讨了空间锥体目标的特征提取与识别问题。首先建立微动目标多散射中心回波信号模型。通过对目标与诱饵的微多普勒特性的分析指出,虽然二者回波信号的微多普勒谱均为线谱,但谱线间隔以及谱线幅度由于微动特性的不同存在差异。因此,文中提出应用低分辨雷达多次回波数据提取微多普勒域熵与标准差作为识别特征,对目标与诱饵进行分类识别。
2.微多普勒数学模型
锥体目标微动模型如图1所示。坐标系(U,V,W)与坐标系(X,Y,Z)平行。雷达位于坐标系(U,V,W)的原点Q.坐标系 (X,Y,Z)的原点O为目标的质心。点O在雷达坐标系中的位置为:R0=R0(cosαcosβ,sinαcosβ,sinβ)T,其中,α、β分别表示方向角与俯仰角。若目标上任一散射点i在(X,Y,Z)坐标系下的初始位置为r0=(X0,Y0,Z0)T.经过t时刻,点i运动至i′,点O运动至O′.此时点i的坐标为:

图1 锥体目标微动模型
rt=(Xt,Yt,Zt)T=M(t)r0
(1)
式中,M(t) 表示3×3 目标微动变换矩阵。令时刻t雷达与点i的矢量距离为Ri(t),若目标的平动速度为v,则雷达与点i的标量距离Ri(t) 可表示为
Ri(t) =|Ri(t)|
≈R0+vtcosγ+Xtcosαcosβ+
(2)
Ytsinαcosβ+Ztsinβ
式中:γ为速度与雷达视线的夹角; |·|表示欧几里德范数。
若雷达发射载频为fc的正弦波,接收的回波基带信号可以表示为
si(t)=ρiexp(jΦ(Ri(t)))
(3)
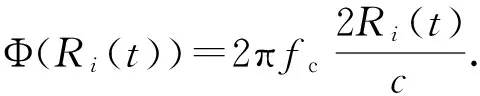
(4)
由于空间目标外形结构比较简单,可以应用强散射中心信号模型计算回波[5,12]。对于有N个强散射中心的目标,接收回波基带信号可以表示为
(5)
3.微多普勒特性分析
3.1 摆动目标的微多普勒特性
摆动模型如图2所示。目标以OC为轴在平面OZC内摆动,摆动频率为fb(角速度ωb=2πfb)。摆动角θb(t)=Θbsin(2πfbt),其中Θb表示最大摆动角。摆动目标的微动变换矩阵可以表示为
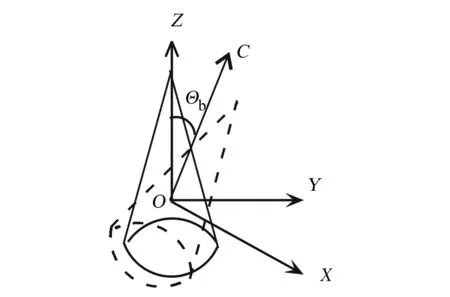
图2 锥体目标摆动模型
(6)
将式(1)、(2)、(6)代入到式(3),则t时刻第i个散射点的回波信号为
si(t)=Aexp[j2πfdt]exp[jysin(θb(t)+χ)]
(7)
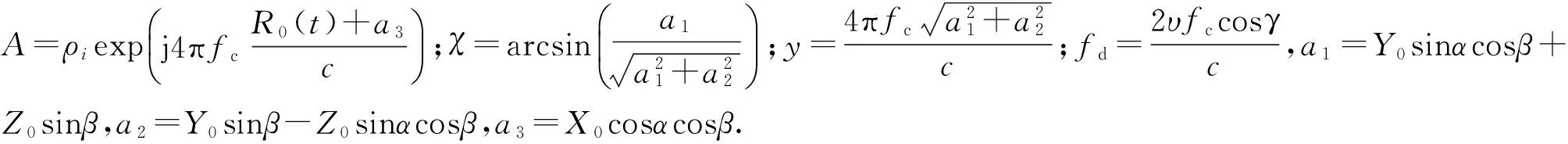
(8)
式中,J(·) 是第一类Bessel函数。令g(t)=exp(jysin(θb(t)+χ)),则该式傅立叶级数展开形式为
g(t) =exp(jysin(θb(t)+χ))
(9)
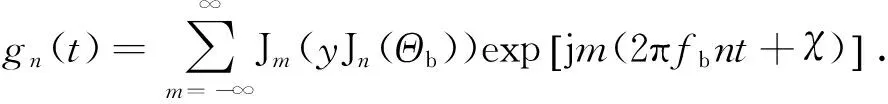
exp(jmx)δ(f-mnfb)
(10)
由式(10)可知,信号gn(t) 的频谱为一系列Dirac函数之和,即由一系列间隔为nfb(n=-N,…-1,0,1,…,N)谱线构成。令G(f) 为g(t)的傅立叶变换,则g(t)的频谱为
G(f) =G-N(f)*…*G1(f)*…*GN(f)
=G1(f)*[G-N(f)*…*GN(f)]
(11)
式中*表示卷积。由于G1(f) 由一系列间隔为fb的Dirac函数构成,因此,G(f)为谱线间隔为fb的线谱。令Si(f)为si(t)的傅立叶变换。对于有N个强散射中心的目标,回波信号的频谱为S(f)。
Si(f) =AG(f-fd),S(f)
(12)
根据式(12),目标的摆动调制使得回波中产生了相应的微多普勒效应。其信号的频谱是一系列Dirac函数之和,即由一系列以fd为中心,周期为fb的谱线构成。谱线的周期仅由目标的摆动频率fb决定,谱线的幅度由散射点的位置、散射点数目、雷达参数以及Bessel函数决定。
3.2 进动目标的微多普勒特性
进动模型如图3所示。目标绕其自身对称轴OZ自旋, 同时绕方向矢量OC锥旋。OZ与OC的交点为O,二者的夹角被称为进动角。进动可分解为自旋与锥旋两类运动,因此进动目标的微动变换矩阵为[13]

图3 锥体目标进动模型
M(t)=Mc(t)Mr(t)
(13)
锥旋变换矩阵
Ri(t)≈R0+vtcosγ+b1cos(ωct-ωrt)+
b2cos(ωct+ωrt)+b3sin(ωct+ωrt)+
b4sin(ωct-ωrt)+b5sin(ωct)+b6sin
(ωrt)+b7cos(ωrt)+b8cos(ωct)+b9
(14)
式中b1~b9由目标的散射点位置与雷达视线共同决定。将式(14)代入式(3),可求得t时刻点i回波。对该回波信号进行傅立叶级数展开,有
(15)
q=k1+k2+k7+k8
n=-k1+k2+k3-k4+k6+k7
m=k1+k2+k3+k4+k5+k8
式中:
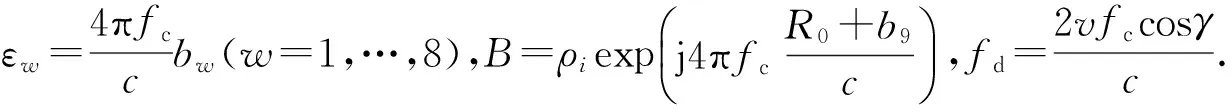
mfcr-nfr-fd)
(16)

(17)
根据式(17), 目标的进动使得回波中产生了相应的微多普勒效应。多散射点进动目标信号的频谱是一系列Dirac函数之和。谱线的间隔由目标的自旋频率fr以及锥旋频率fcr共同决定,谱线幅度由散射点的位置、雷达参数和Bessel函数决定。
自旋可以视为锥旋角速度等于0的进动。因此,多散射点自旋目标信号的频谱是一系列Dirac函数之和。谱线的间隔等于目标的自旋频率fr,谱线幅度由散射点的位置、雷达参数和Bessel函数决定。
4.识别特征抽取

(a) 摆动目标fb=3 Hz
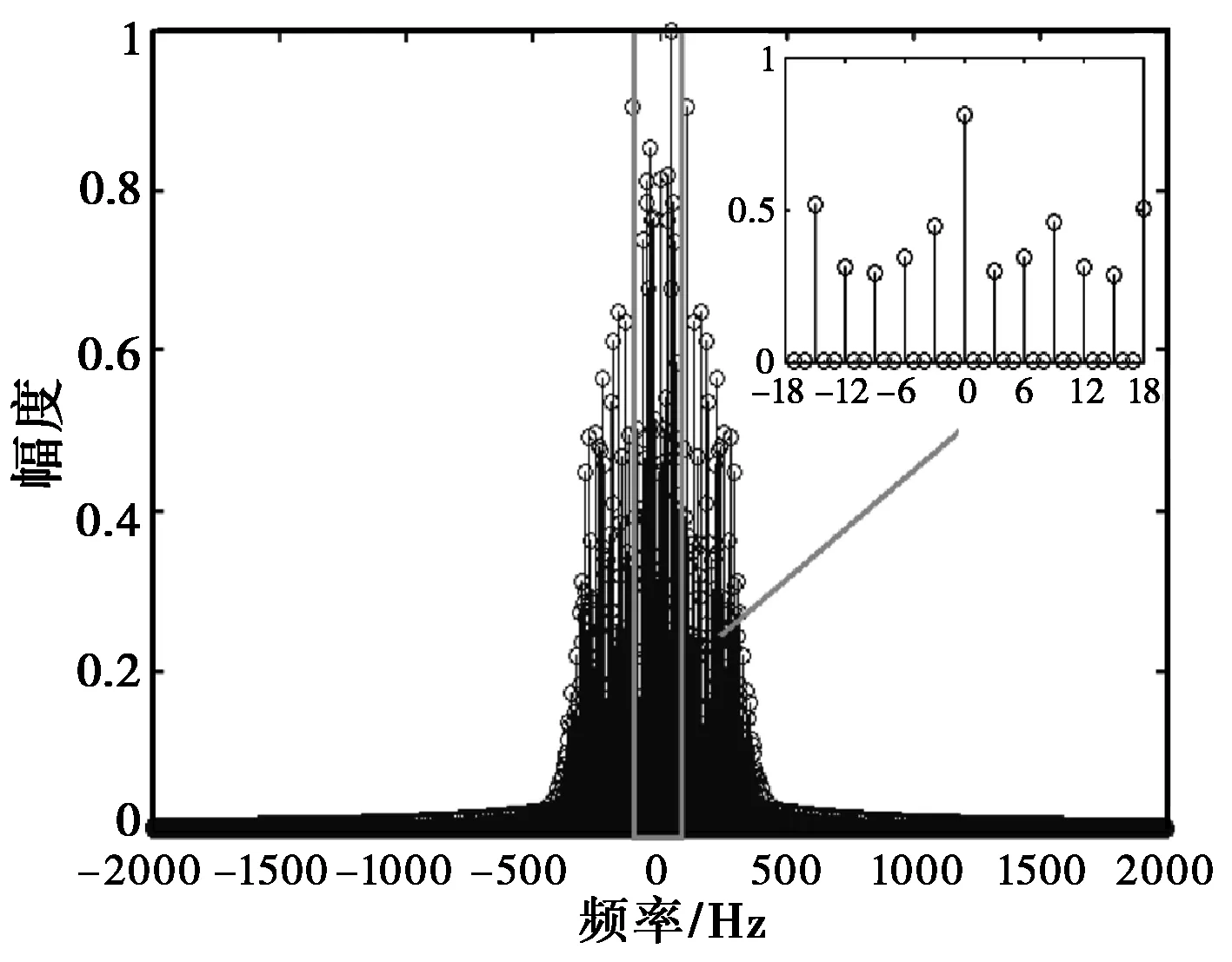
(b) 自旋目标 fr=3 Hz
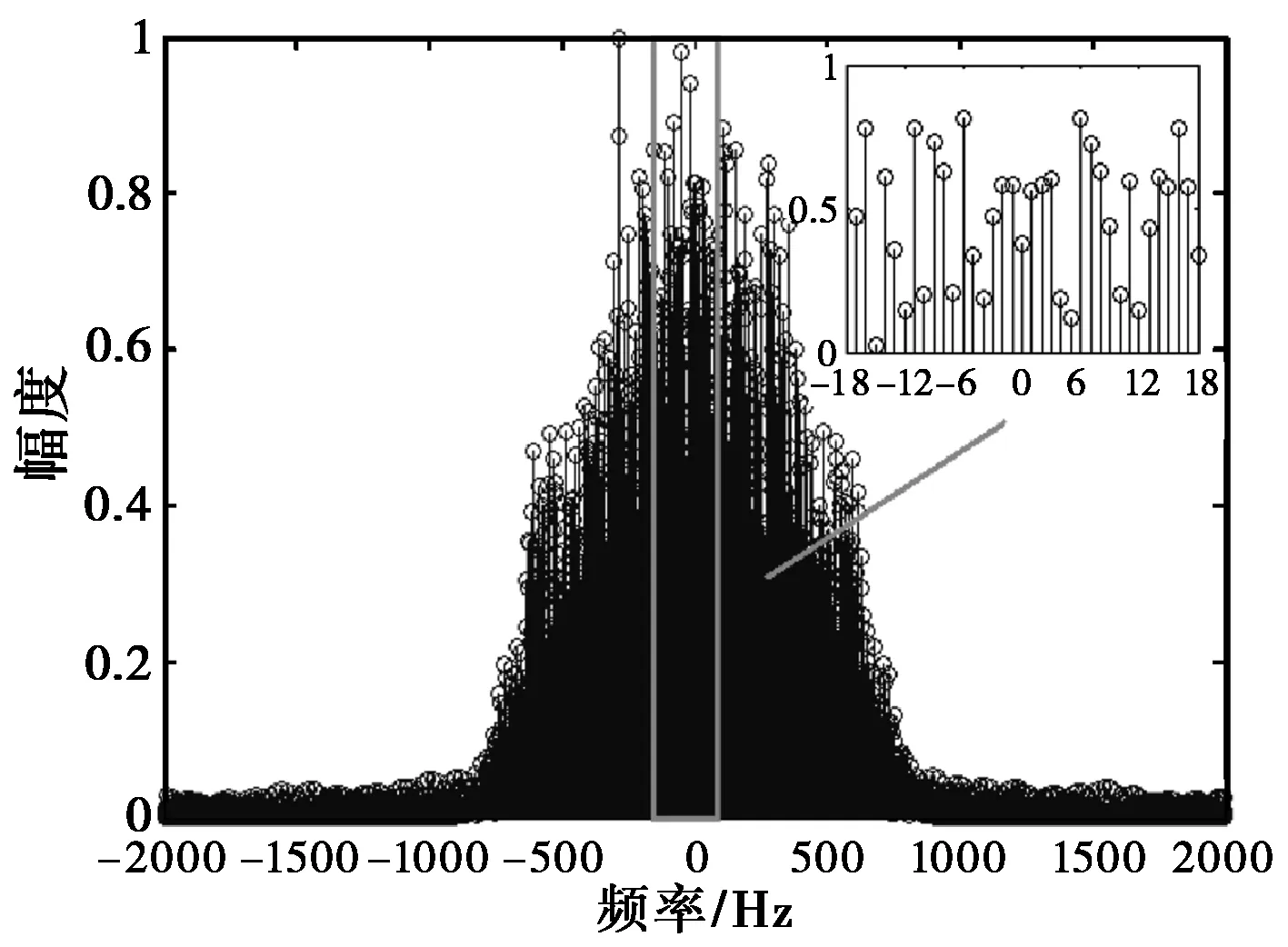
(c) 进动目标fr=5 Hz,fcr=3 Hz图4 三类微动目标的多普勒谱
图4分别给出了经过平动补偿后的摆动目标、自旋目标以及进动目标的多普勒谱。目标高度为2 m,底面半径为0.4 m,存在23个强散射点。雷达载频为10 GHz.图4(a)为摆动目标多普勒谱,摆动频率为3 Hz,摆动角为10°.从中可以发现,谱线分布于3 Hz、6 Hz等摆动频率整数倍的位置;图4(b)为自旋目标的多普勒谱,自旋频率为3 Hz.可以发现谱线分布于3 Hz、6 Hz等自旋频率整数倍的位置;4(c)显示了进动目标的多普勒谱,自旋频率为5 Hz,锥旋频率为3 Hz,进动角为10°.从中可以发现,谱线位于1 Hz、2 Hz等自旋频率与锥旋频率组合的位置,与第3节的理论分析一致。结合第3节的分析可知,在目标外形相近的情况下,进动目标的多普勒谱宽最宽且谱线的分布间隔更复杂,与自旋目标、摆动目标的多普勒谱存在明显差异。这种特性可以作为识别的依据。回波信号的多普勒谱确实反映了目标微动的主要特性,因此基于回波信号多普勒谱的差异能够对进动、摆动与自旋目标进行识别与分类。
进一步分析图4,可以发现以下两点:1)由于进动为合成运动,进动目标的回波信号的微多普勒谱谱线位置由自旋频率与锥旋频率共同决定,使得其回波的微多普勒域能量分布比较分散;而摆动目标(自旋)运动简单,谱线间隔仅由其摆动(自旋)频率决定,使得其回波的微多普勒域能量分布相对集中。因此,进动目标的谱线间隔必然较摆动目标的谱线间隔更复杂,其微多普勒的分布也更广泛。可以提取微多普勒的熵值来描述这种特征。2)进动目标回波信号的多普勒谱的谱宽要大于自旋目标与摆动目标回波的多普勒谱谱宽,且进动目标的谱线间隔较摆动(自旋)目标的谱线间隔更复杂,其微多普勒谱线的分布也更广泛。基于以上事实,可以应用频域波形标准差来描述这种差异。

1) r进制的熵定义为
(18)
熵是描述变量的平均不确定性的物理量,可用式(18)定义的熵表征微多普勒谱能量的散布程度。微多普勒谱能量的散布程度越大,其熵值会越大,微多普勒谱能量的散布程度越小,其熵值也会越小。
2) 标准差定义为
(19)

图5(看412页)显示了进动目标、摆动目标与自旋目标微多普勒域熵-微多普勒域波形标准差的二维特征矢量图。目标微动参数如表1所示。从图5可见,进动目标、自旋目标以及摆动目标的微多普勒域熵-标准差存在明显差异。进动目标微多普勒域熵的范围在为6.9~10.3,摆动目标微多普勒域域熵的范围为0.1~4.8,自旋目标微多普勒域域熵的范围为4.6~7.2,进动目标的微多普勒域熵大于自旋目标与摆动目标的微多普勒域熵;进动目标微多普勒域标准差的范围为2.2~8.2,摆动目标微多普勒域标准差的范围为14.2~62.1,自旋目标微多普勒域标准差的范围为6.8~30.1.以上数据与分析一致。因此,应用微多普勒域熵以及波形标准差可以作为识别特征。

表1 目标微动参数以及雷达视线(散射点数目7~19,目标高度范围为1.8~2.2 m)
5.仿 真
目标为多散射中心的模型,散射点散射强度服从N(0,1)的正态分布,初始相位服从U[0,2π]均匀分布。目标高度变化范围为1.8~2.2 m,散射点数目变化范围为7~19。实验中分别设置了进动目标、自旋目标以及摆动目标。由于空间目标多为轴对称结构,存在散射点遮挡效应。雷达载频10 GHz,脉冲重频4000 Hz,波束驻留时间1 s.
本文从三个方面验证了识别特征的稳健性。这三方面分别为:分类器对识别性能影响、噪声对识别性能影响以及微动参数对识别性能影响。为检验分类器对识别性能的影响,应用支持向量机分类器(SVM)以及K近邻分类器(K-NN)两种分类器进行分类。SVM分类器采用高斯核K(xi,xj)=exp(-‖xj-xi‖2/σ2).在计算负担允许的条件下选用了不同的核参数进行实验,文中给出的识别率结果是在有限次实验中最好的识别结果。KNN分类器近邻数为3.
仿真1:噪声对识别性能的影响
通过测试噪声对识别性能的影响检验识别特征的稳健性。实验中目标微动分别为进动、摆动与自旋,改变微动参数,各获得1080个目标。每个微动目标在波束驻留时间内接收的回波作为一个样本。训练样本与测试样本的微动参数如表2与表3所示(方向角在0~180°随机变化,俯仰角在0~90°随机变化)。作为训练样本的回波无噪声影响,而作为测试样本的回波受加性高斯白噪声影响。

表2 训练样本参数设置

表3 测试样本参数设置
图6给出了识别率随信噪比变化曲线。从图6可知,以无噪声环境下的数据作为训练样本,不同信噪比条件下的数据作为测试样本,两种分类器均显示了良好的性能。证明了微多普勒域熵与波形标准差作为识别特征能够有效地实现目标与诱饵的分类。

图6 不同信噪比下的识别率曲线
仿真2:微动参数对识别性能的影响,SNR=5 dB
通过微动参数对识别性能的影响检验识别特征的稳健性。训练样本与测试样本的微动参数不同。实验中进动目标、自旋目标以及摆动目标的微动参数如表1所示。对于每类目标,通过改变微动参数,各获得了1080个目标作为样本。样本中随机选取1/3作为训练样本,其余的2/3作为测试样本。
图7给出了识别率随测试样本变化的曲线。从图7可知,训练数据与测试数据的微动参数不同,应用微多普勒域熵与波形标准差作为识别特征,两类分类器的识别率均高于97%。因此可以得出结论微动参数的变化对识别性能的影响十分有限,证明了微多普勒域熵与波形标准差作为识别特征能够有效地实现目标与诱饵的分类。
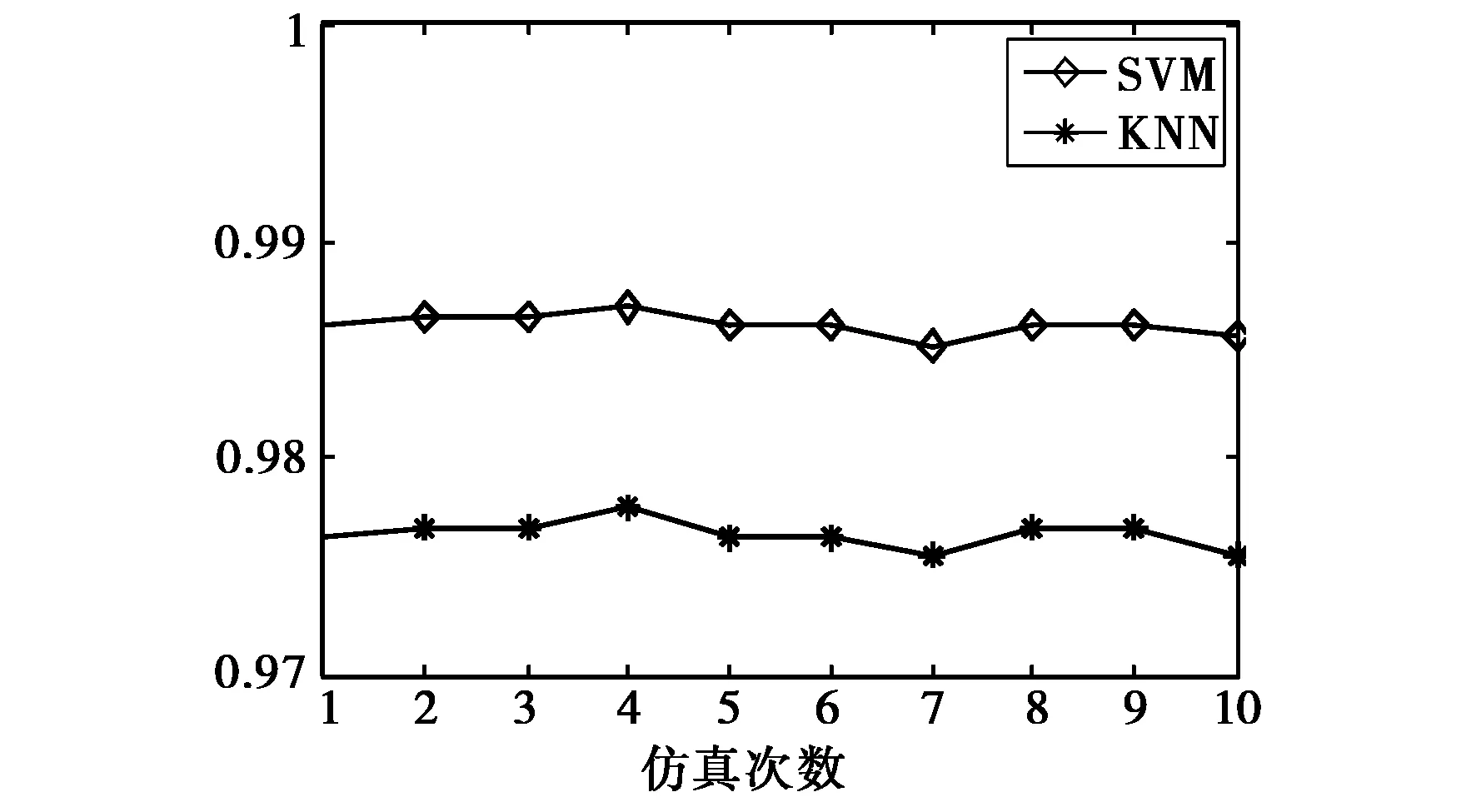
图7 不同测试样本下的识别率曲线 SNR=5 dB
综合仿真1与仿真2可以得出结论,微多普勒域熵与波形标准差作为一种稳健的识别特征,能够实现目标与诱饵的识别。
6.结 论
本文研究了空间锥体真假目标的识别问题。首先建立了目标多散射中心模型,分析了空间锥体目标的微动以及回波信号的微多普勒特性。基于目标微多普勒特性的差异,提出从回波信号抽取微多普勒域熵与波形标准差作为识别特征的分类方法。从三个方面即分类器对识别性能影响、噪声对识别性能影响以及微动参数对识别性能影响验证了识别特征的稳健性。实验结果证实了文中所提特征能够有效地实现目标与诱饵的识别。
[1] CHEN V C, LI F, HO S S, et al. Micro-Doppler effect in radar: phenomenon, model, and simulation study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1):2-21.
[2] CHEN V C, LI F, HO S S, et al. Analysis of micro-Doppler signatures[J]. IEE Proc.-Radar Sonar Navig., 2003, 150(4):271-276.
[3] 童创明, 王光明, 张晨新, 等. 喷气发动机的J.E.M效应调制谱分析[J]. 电波科学学报, 1999, 14(2):136-143.
TONG Chuangming, WANG Guangming, ZHANG Chenxin, et al. Analysis of J.E.M effect modulation spectra of jet engine[J]. Chinese Journal of Radio Science, 1999, 14(2): 136-143. (in Chinese)
[4] 杨立明, 曹祥玉. 直升机旋翼对回波的调制效应分析[J]. 电波科学学报, 2002, 17(1):93-96.
YANG Liming, CAO Xiangyu. Analysis of the modulation effect of the backscattered wave from a helicopter rotor[J]. Chinese Journal of Radio Science, 2002, 17(1):93-96. (in Chinese)
[5] CUOMO K M, PIOU J E, MAYHAN J T. Ultra-wideband coherent processing[J]. The Lincoln Laboratory Journal, 1997, 10(2):203-222.
[6] NUNN E C. The US Army white sands missile range development of target motion resolution[C]//Processing of IEEE electronics and Aerospace Systems Conventions. Arlington, USA: IEEE Press, 1980:346-352.
[7] 庄钊文, 刘永祥, 黎 湘. 目标微动特性研究进展[J]. 电子学报, 2007, 35(3):520-525.
ZHUANG Zhaowen, LIU Yongxiang, LI Xiang. The Achievements of target characteristic with micro-motion[J]. Acta Electronica Sinica, 2007, 35(3):520-525. (in Chinese)
[8] S-band radar micro-Doppler signatures for BMD discrimination[DB/OL].http://www.acq.osd.mil/osbp/sbir/solicitations/sbir044/mda044.htm,2003-10-16/2004-08-24.
[9] 孙慧霞, 刘 峥, 薛 宁.自旋进动目标的微多普勒特性分析[J]. 系统工程与电子技术, 2009, 31(2):67-70.
SUN Huixia, LIU Zheng, XUE Ning. Micro-Doppler analysis of spinning-precession target[J]. Systems Engineering and Electronics, 2009, 31(2):67-70. (in Chinese)
[10] 陈建文, 李士国. 基于目标运动分辨技术提取导弹目标运动特征[J]. 现代雷达, 2003, 25(6):5-7.
CHEN Jianwen, LI Shiguo. Missile motion feature extraction based on target motion resolution[J]. Modern Radar, 2003, 25(6): 5-7. (in Chinese)
[11] 陈行勇, 黎 湘, 郭桂蓉. 微进动弹道导弹目标雷达特征提取[J]. 电子与信息学报, 2006, 28(4): 643-646.
CHENG Hangyong, LI Xiang, GUO Guirong. Radar feature extraction of micro-precession ballistic missile warhead[J]. Journal of Electronics & Information Technology, 2006, 28(4):643-646. (in Chinese)
[12] MAYHAN J T. RCS scatterer extraction using apriori target information[R]. ESC-TR-2003-078, 2004, Lincoln Laboratory:1-40.
[13] 高红卫, 谢良贵, 文树梁. 基于微多普勒特征的真假目标雷达识别研究[J]. 电波科学学报, 2008, 23(4):16-20.
GAO Hongwei, XIE Lianggui, WEN Shuliang. Research on radar identification of ballistic missile warhead and decoys based on micro-Doppler signature[J]. Chinese Journal of Radio Science, 2008, 23(4):16-20. (in Chinese)

