空间不合成平板端射阵列副瓣研究

刘姜玲 刘姜涛 王小谟

(1.北京理工大学信息与电子学院，北京 100081；2.湖北第二师范学院物理与电子信息学院，湖北 武汉 430205；3.中国电子科学研究院，北京 100041)

1. 引 言

端射天线有很多优点，比如容易制作、价格低廉，并且有好的空气气动性。端射天线特别适用于高速飞行器[1]。可是传统意义上的端射天线是中等增益的天线，并不适用于雷达探测系统的要求。为了提高方向性和增益，用平板端射天线作为单元进行了组阵研究，发现平板端射天线的组阵不符合常规天线组阵理论。端射天线阵的增益随着天线单元间距的增大而提高，并且间距在1.5λ时天线阵列的增益最高，但同时引入栅瓣问题[2]。可以通过不均匀布阵抑制栅瓣。

以往针对不均匀布阵问题开展了大量研究，天线间距按0.5λ栅格稀布，取得了大量研究成果，如传统的Chebyshev-Dolph综合法[3]、泰勒综合法[3]、动态规划法[4]、模拟退火法[5]、遗传算法[6]等。但对天线间距按1.5λ栅格稀布的阵列的优化还没有开展过相关研究。

本文为解决平板端射天线高增益布阵问题，针对最小天线间距大于1.5λ的阵列优化开展了研究工作，发现当天线单元最小间距为1.5λ时，由于强栅瓣的出现，通过优化天线间距无法获得低副瓣。因此，提出一种新的阵列组阵方法，即在发射时采用正交信号，发射波束在空间不合成，能量全向辐射，在接收端通过数据处理形成发射和接收双程方向图，通过优化阵列总方向图，成功解决了天线最小间距大于1.5λ的阵列栅瓣和高副瓣问题。把正交波形多输入多输出(MIMO)阵列优化布阵研究[7-8]拓展至分布式MIMO阵列优化问题。

2.天线间距大于1.5 λ的阵列优化

2.1 阵列模型及适应度函数改进

为讨论方便，以图1所示对称结构稀布线阵为例。阵元数为2N+1(N为正整数)，所有阵元相同且均匀等幅激励，阵元位置d0=0，d-N=-L，dN=L，dc为最小阵元间距，di=xi+idc，1≤i≤N-1，0≤xi≤L-Ndc，其中L为约束阵列半孔径。

图1 对称稀布线阵的阵列模型

阵元无方向性时的方向图为

-π/2≤θ≤π/2，k=2π/λ

(1)

以x为决策变量的改进适应度函数为

fitness(x1，x2，…，xN-1)=max|f(θ)/Fmax|

(2)

式中：Fmax是主瓣峰值；θ取值区间需排除主瓣区域。目标函数为

f(x1，x2，…，xN-1)=min{fitness(x1，x2，…，xN-1)}

2.2 阵列峰值副瓣分析

Kennedy和Eberhart在1995年提出粒子群算法，该算法通过群体中粒子间的合作与竞争产生的群体智能来指导优化搜索，可适用于非线性优化问题，收敛速度快，设置参数少，程序实现简单，近年来被广泛应用于解决天线阵列优化问题[9]。

采用改进的粒子群算法对具有不同间距约束的稀布阵列进行优化仿真，发现间距不同时，优化效果差异很大。

2.2.1 优化算法有效性验证

总阵元数为17的对称阵，阵元间距约束为0.5λ，优化后的阵列方向图如图2所示，峰值旁瓣电平(PSLL)为-19.89 dB.文献[10]和[11]优化的PSLL是-19.49 dB，验证了本文改进粒子群优化算法的有效性。

图2 最小间距为0.5 λ的17元不均匀阵最优方向图

2.2.2 仿真分析

针对不同最小阵元间距约束和不同阵元数的阵列开展了优化仿真。图3为阵列副瓣随着天线最小阵元间距变化而变化的曲线，其中实线表示17元天线阵列，虚线表示33元天线阵列。由图3可知，随着天线间距逐渐拉大，优化布阵后所得PSLL越来越高，最小间距0.5λ的17元阵列为 -19.9 dB，1.5λ时高达-7.029 dB.图4为阵列副瓣随着天线单元数变化而变化的曲线，其中实线表示最小阵元间距约束为1.5λ的天线阵列，虚线表示最小阵元间距约束为0.5λ的天线阵列。由图4可知，通过增加阵元数优化后PSLL有所降低，当单元数增加到40以上时，PSLL几乎保持不变，最大降幅约为5 dB，但由于间距拉大而导致的副瓣增加的最大增幅约为12 dB.

图3 优化布阵后PSLL随最小天线间距变化的曲线

图4 优化布阵后PSLL随阵元数变化的曲线

由上述分析可知：

1) 天线最小间距为0.5λ的稀布阵列，通过优化天线间距布阵，可以实现低PSLL；

2) 随着天线间距的加大，优化后PSLL越来越差，当天线最小间距约束拉大到1.5λ时，通过优化天线间距布阵可以抑制栅瓣，但同时引入高PSLL；

3) 通过增加阵元数，能降低PSLL，但降低幅度远小于由于间距拉大而导致的PSLL增高的幅度；

4) 通过常规稀布阵列优化无法解决天线最小间距约束为1.5 λ时的高峰值旁瓣问题。

3.空间不合成阵列的优化

常规不均匀优化布阵无法解决最小天线间距为1.5λ时的高旁瓣问题，因此，本文提出一种新的组阵思路即空间不合成阵列。

3.1 空间不合成阵列模型

发射天线采用正交信号激励，空间能量全向分布，发射信号在空间不形成定向辐射，在接收端通过补偿发射和接收延迟进行同相相加，合成等效发射波束和接收波束。

假设阵列有M个发射阵元，N个接收阵元，第m个发射阵元的权值为wtm，发射信号频率为fm，振幅为gt，则发射阵列信号矢量可以表示为

vt= [wt1gtexp(-j 2πf1τt1)，wt2gtexp(-j 2πf2τt2)，

…，wtMgtexp(-j2πfMτtM)]

设第n个接收阵元的权值为wrm，振幅为gr，则接收阵列信号矢量可以表示为：

vr= [wr1grexp(-j 2πfτr1)，wr2grexp(-j 2πfτr2)，

…，wrNgrexp(-j 2πfτrN)]

信号从第m个发射阵元传播到目标散射点，然后再到第n个接收阵元，其相对于发射和接收参考点的相对延迟时间可以表示为τmn=τtm+τrn，其中τtm、τrn分别为第m个发射阵元到目标和目标到第n个接收阵元间的延时，具体与阵列形状有关。

则接收阵列的输出矢量为v=vt⊗vr，其中⊗是Kronecker积，输出矢量v中共有MN项，则整个接收阵列的输出为各项之和，可表示为

(-j2πfτrn)

=Ft(θ)⊗Fr(θ′)

(3)

对式(3)归一化后可得到空间阵列的合成方向图

(4)

Gt(θ)和Gr(θ′)分别为发射阵列和接收阵列的方向图，阵列总方向图为收发方向图相乘。

收发天线分置，2M+1个发射天线和2N+1个接收天线分别按图1所示布置，所有阵元相同且均匀等幅激励，天线指向为0度的阵元无方向性时的阵列总方向图为

f(θ)= (1+2cos(2πfMLsinθ/c)+

(1+2cos(2πfLsinθ/c)+

-π/2≤θ≤π/2，0≤xtm，xrn≤L-Ndc

(5)

空间不合成阵列的适应度函数为

fitness(xt1，xt2，…，xt，M-1，xr1，xr2，…，xr，N-1)

=max|f(θ)/Fmax|

(6)

式中：Fmax是主瓣峰值；θ取值区间需排除主瓣区域。目标函数为

f(xt1，xt2，…，xt，M-1，xr1，xr2，…，xr，N-1)

=min{fitness(xt1，xt2，…，xt，M-1，xr1，xr2，…，

xr，N-1)}

3.2 空间不合成阵列峰值副瓣分析

对改进粒子群优化软件进行修改，适应度函数采用式(6)的双程方向图函数，对空间不合成阵列天线进行优化布阵研究。

以收发天线为分置的17元不均匀线阵为例，天线最小间距为最小波长的1.5倍，激励信号为步进频信号，起始频率f0为3 GHz，频率步长1 MHz，频率步数17.入射角和目标角均为0度。优化后的PSLL见表1，比常规17元不均匀阵降低22.095 dB，比常规35元不均匀阵降低19.994 dB，在抑制栅瓣的同时，大大降低了PSLL.

表1 各阵列优化后的PSLL比较

对最小间距为1.5λ的不同阵元数的空间不合成阵列开展了大量仿真计算，阵列峰值副瓣随天线单元数变化而变化的规律如图5所示。发现随着阵元数的增加峰值副瓣逐渐降低，当阵元数增加到一定数目后PSLL几乎保持不变，约为-31 dB.

当阵列入射角和目标角不为0度即存在扫描角时，阵列PSLL随扫描角度的增大而抬高，变化曲线如图6所示。由图6可知，当扫描角≤±10°时，PSLL仅抬高3.6 dB，阵列能实现扫描。

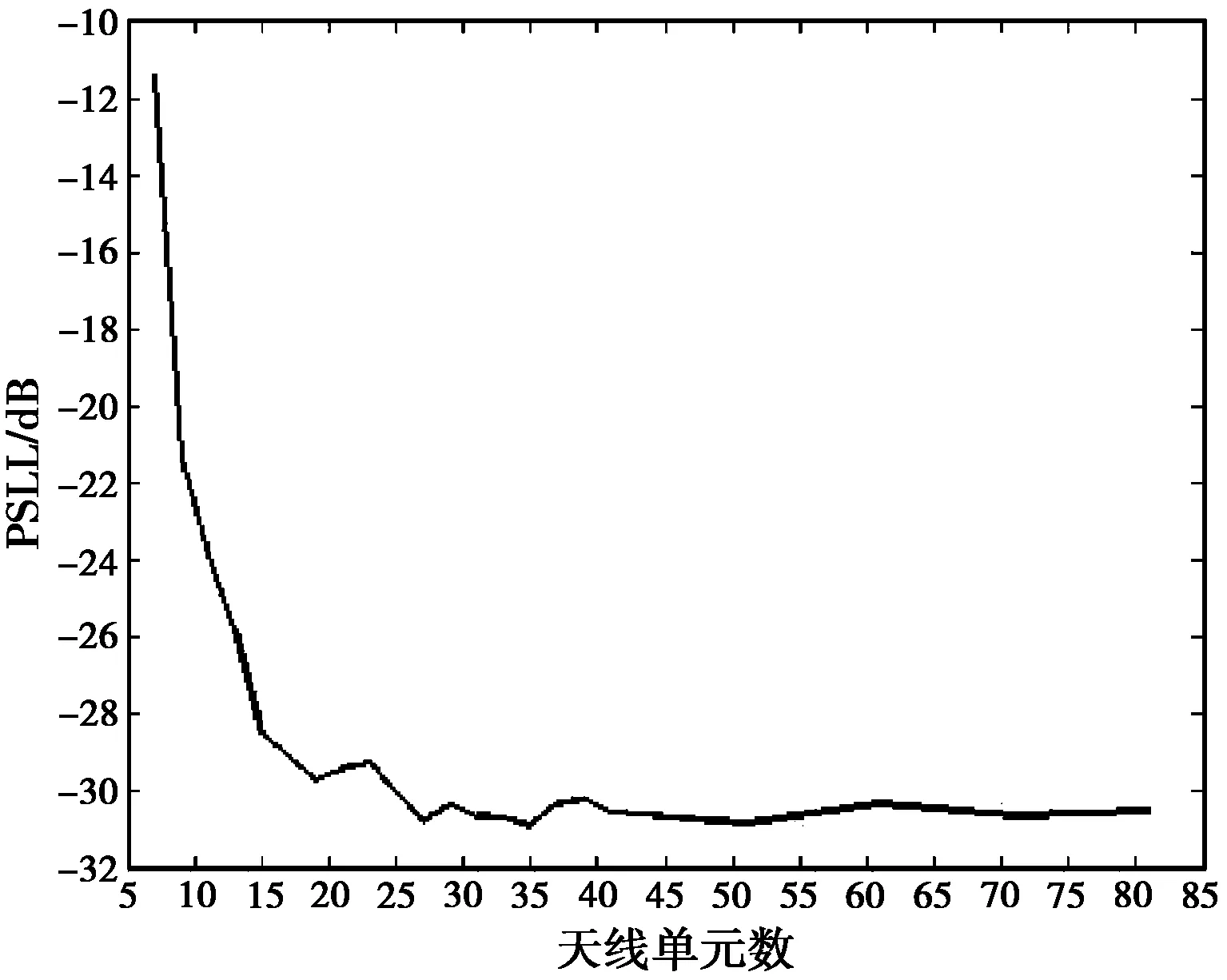
图5 优化布阵后PSLL随阵元数变化的曲线

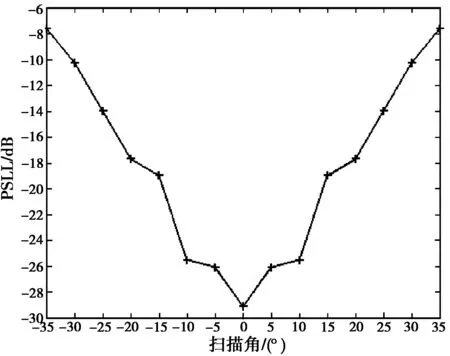
图6 优化布阵后PSLL随阵列扫描角变化的曲线

4.结 论

本文为解决平板端射天线高增益布阵问题，针对天线间距大于1.5λ的阵列优化开展了研究工作，把稀布阵列优化问题拓展到最小天线间距大于1.5λ的情况。当天线单元最小间距为1.5λ时，由于强栅瓣的出现，按常规不均匀阵列优化原理开展优化布阵，可以抑制栅瓣但无法解决引入的高旁瓣问题。提出采用空间不合成组阵新原理，针对该新型不合成阵列展开最小间距大于1.5λ的阵列布阵优化，在抑制栅瓣的同时成功实现了低旁瓣。为平板端射天线的研制提出了一条新思路。

[1] 737 AEW &C Wedgetail Airborne Early Warning and Control Aircraft [OL]. USA, 2008 [2008-09-26],http://www.airfare-technology.com/projects/737aewc/.

[2] 姚国伟, 薛正辉, 李伟明, 等. 平板端射天线组阵的研究[J]. 电波科学学报, 2009, 24(2): 323-326.

YAO Guowei, XUE Zhenghui, LI Weiming, et al. The research of plate end-fire antenna [J]. Chinese Journal of Radio Science, 2009, 24(2): 323-326. (in Chinese)

[3] 谢处方, 邱文杰. 天线原理与设计[M]. 西安：西北电讯工程学院业出版社, 1985: 109-118.

XIE Chufang, QIU Wenjie. Theory and design of antenna[M]. Xi’an: Northwest Telecommunication Engineering College publishing company, 1985: 109-118. (in Chinese)

[4] SKOLNIK M I, NEMHAUSER G, SHERMAN J W. Dynamic programming applied to unequally spaced arrays[J]. IEEE Trans Antennas Propagat, 1964, AP-12 (1): 35-43.

[5] MURINO V, TRUCCO A, REGAZZONI C S. Synthesis of unequally spaced arrays by simulated annealing[J]. IEEE Trans Antennas Signal Processing, 1996, 44 (1): 119-123.

[6] 陈客松, 韩春林, 何子述. 一种有阵元间距约束的稀布阵天线综合方法[J]. 电波科学学报, 2007, 22(1): 27-32.

CHEN Kesong, HAN Chunlin, HE Zishu. A synthesis technique for linear sparse arrays with optimzation constraint of minimum element spacing[J]. Chinese Journal of Radio Science, 2007, 22(1): 27-32. (in Chinese)

[7] 胡亮兵, 刘宏伟, 杨晓超, 等. 集中式MIMO雷达发射方向图快速设计方法[J]. 电子与信息学报, 2010, 32(2): 481-484.

HU Liangbing, LIU Hongwei, YANG Xiaochao, et al. Fast transmit beampattern synthesis for MIMO radar with colocated antennas[J]. Journal of Electronics & Information Technology, 2010, 32(2): 481-484. (in Chinese)

[8] 胡亮兵, 刘宏伟, 刘保昌, 等. MIMO雷达发射方向图匹配和波形优化方法[J]. 西安电子科技大学学报(自然科学版), 2009, 36(6): 1021-1026.

HU Liangbing, LIU Hongwei, LIU Baochang, et al. Transmit beampattern matching design and waveform optimization for MIMO radar [J]. Journal of Xidian University (Natural Science), 2009, 36(6): 1021-1026. (in Chinese)

[9] 焦永昌, 杨 科, 陈胜兵, 等. 粒子群优化算法用于阵列天线方向图综合设计[J]. 电波科学学报, 2006, 21(1): 16-20.

JIAO Yongchang, YANG Ke, CHEN Shengbing, et al. Application of particle swarm optimization in antenna array pattern synthesis[J]. Chinese Journal of Radio Science, 2006, 21(1): 16-20. (in Chinese)

[10] KUMAR B P, BRANNER G R. Design of unequally spaced arrays for performance improvement [J]. IEEE Trans Antennas Propagat, 1999, 47 (3): 511-523.

[11] KUMAR B P, BRANNER G R. Generalized analytical technique for the synthesis of unequally spaced arrays with linear, planar, cylindrical or spherical geometry [J]. IEEE Trans Antennas Propagat, 2005, 53 (2): 621-634.