基于新的相关性组合预测模型构建
袁宏俊,胡凌云
(安徽财经大学 a.统计与应用数学学院;b.管理科学与工程学院,安徽 蚌埠 233030)
0 引言
由于每种预测方法利用的数据源不尽相同,不同的数据源都是从不同的角度提供各方面有用的信息,因此每种预测方法之间并不是相互排斥的,而是相互联系、相互补充的。在预测的过程中,如果想当然地认为某个单项预测方法的预测误差较大,就把该种预测方法弃之不用,这可能造成部分有用的信息丢失,因此,Bates.J.M.和Granger.C.W.J.于l969年首次系统提出组合预测方法。由于组合预测方法能有效地提高预测精度,一直是国内外预测界研究的热点课题之一,并取得了大量的研究成果[1~8]。文献[4]针对无非负约束的以误差平方和达到最小的最优组合预测模型,提出了劣性组合预测、非劣性组合预测、优性组合预测的概念,并利用组合预测绝对误差信息矩阵的性质判断简单平均方法是非劣性组合预测、优性组合预测的条件。文献[5]给出了研究组合预测方法的另一新途径,即提出了四种基于相关性指标的最优组合预测模型的研究,与传统的组合预测方法有较大的差别。本文拟在现有文献的基础上,提出一种新的相关性的组合预测方法,定义算术平均最小贴近度建立最优组合预测模型;在给出优性组合预测、预测方法优超等概念基础上,从理论上研究优性组合预测存在的充分条件、冗余预测方法的存在性及判定方法定理;最后通过实例表明该方法的可行性、有效性。
1 几个基本概念
设某社会经济现象的指标序列的实际值为{xt,t=1,2,…,N},设有m种可行的单项预测方法对其进行预测。xit为第i种预测方法在第t时刻的预测值 (或称拟合值);i=1,2,…,m;t=1,2,…,为传统的实际观测值xt的组合预测值。设L=(l1,l1,…,lm)T为m种单项预测在组合预测中的加权系数向量,它满足由于各预测数据一般不满足归一化,故按决策属性指标无量纲化方法进行处理:
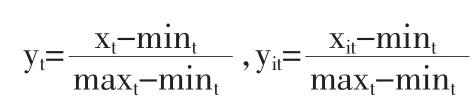
其中 maxt=max{xt,x1t,x2t,…,xmt},mint=min{xt,x1t,x2t,…,xmt}。
显然有 yt,yit∈[0,1],同时
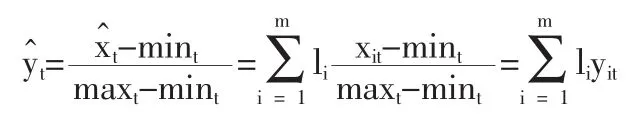

定义 2[9]设 A,B,C∈R(X),且映射 Γ∶R(X)×R(X)→[0,1]满足下列条件:
①Γ(A,B)=Γ(B,A);
②Γ(A,A)=1,Γ(X,⊗)=0;
③若∀x∈X,A(x)≤B(x)≤C(x)或 A(x)≥B(x)≥C(x),有 Γ(A,C)≤Γ(A,B)
则称Γ为R(X)上的贴近度函数,称Γ(A,B)为 A与 B的贴近度,其中R(X)为实函数。
特别地,设 X={x1,x2,…,xn}为序列,A,B∈R(X)为实数序列,不妨定义如下的算术平均最小贴近度Γ(∧表示取小运算):
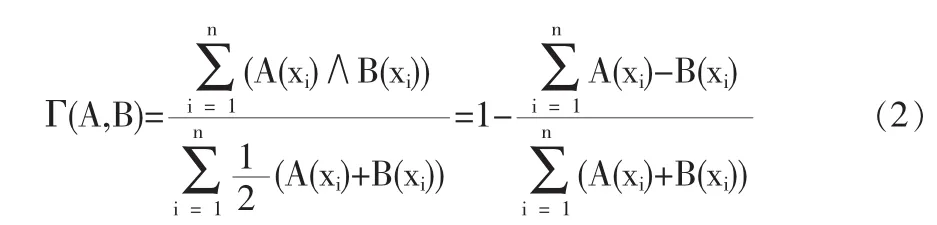
定义3

称Γi(yt,yit)为第i种单项预测方法预测值与指标实际值的算术平均最小贴近度,称Γ(yt,y^t)为组合预测值与指标实际值的算术平均最小贴近度。
组合预测值与实际观测值的算术平均最小贴近度Γ为各种单项预测方法的加权系数l1,l2,…,lm的函数,记为Γ(l1,l2,…,lm)。当从算术平均最小贴近度角度考察组合预测问题时,Γ(l1,l2,…,lm)越大表示组合预测方法越有效。当组合预测值序列与实际观测值序列完全相同时,算术平均最小贴近度达到了最大值1。然而预测误差不可避免,因此,基于新的相关性的算术平均最小贴近度的最优组合预测模型为:

记 Γmin=min{Γi,i=1,2,…,m},Γmax=max{Γi,i=1,2,…,m}
定义 4 若 Γ(l1,l2,…,lm)<Γmin,则称权系数 l1,l2,…,lm确定的组合预测模型为劣性组合预测;若Γmin≤Γ(l1,l2,…,lm)≤Γmax,则称之为非劣性组合预测;若 Γ(l1,l2,…,lm)>Γmax,则称之为优性组合预测。
定义5若第i种、第k种单项预测法的无量纲化指标误差及预测值无量纲化数据满足:

则称基于算术平均最小贴近度下第i种单项预测方法优超第k种单项预测方法,若对任意时刻均有严格的不等号成立,则称第i种单项预测方法严格优超第k种单项预测方法。
定义6若某种单项预测方法在组合预测模型最优权系数中为零,则称该单项预测方法为冗余预测方法。在一个组合预测模型中,设有m种单项预测方法参与组合预测,若最优解中出现冗余方法的个数为m',则称比例系数k=m'/m为组合预测模型的冗余度。
显然0≤k≤(m-1)/m,冗余度越小表示组合预测模型选择的单项预测方法越有效。
2 非劣性组合预测和优性组合预测的存在性定理
定理1基于算术平均最小贴近度组合预测模型(4)的任一满足约束条件的解对应的组合预测至少是非劣性组合预测。
证明:设 L=(l1,l2,…,lm)T为组合预测模型(4)的任一满足约束条件的解,则有:


根据定义4知定理1成立。
推论 在基于算术平均贴近度组合预测模型(4)中,简单平均组合预测的方法一定是非劣性的。
定理 2 假设 Γ1=max{Γi,i=1,2,…,m},eit=yt-y1t≥0,bt∈(-e1t,e1t),若(N+1)×m的线性方程组AL=B存在非负解,则组合预测模型(4)一定存在优性组合预测。其中A=(E,R)T,E=(eit)m×N为无量纲化指标误差信息矩阵,R=(1,1,…,1)T为m维列向量,B=(b1,b2,…,BN,1)T为 N+1 维列向量,L=(l1,l2,…,lm)T为加权系数向量。
证明:设线性方程组AL=B存在非负解L=(l1,l2,…,lm)T,即AL=B,利用矩阵乘法将其写成分量形式为:


由于 bt∈(-e1t,e1t),从而
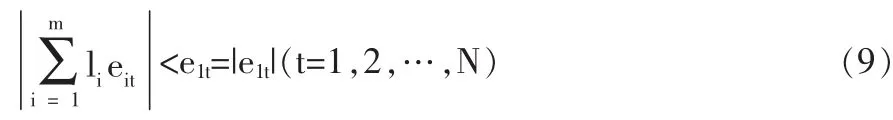
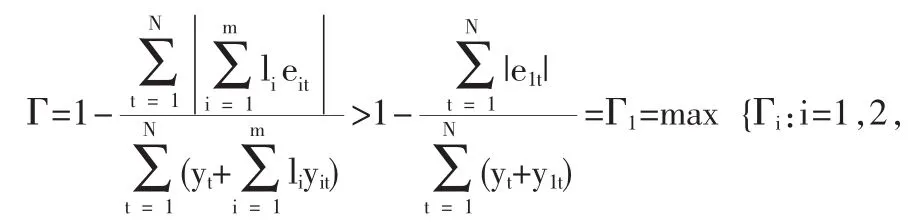
所以:…,m}
根据定义4知定理2成立。
推论 假设 Γ1=max{Γi,i=1,2,…,m},若组合预测模型的无量纲化指标误差信息矩阵E=(eit)m×N中任一列m个元素e1t,e2t,…,emt的算术平均数1,2,…,N),则简单平均组合预测方法是优性组合预测方法。
定理3假设基于算术平均最小贴近度的组合预测模型(4)的冗余度 k<(m-1)/m,则其最优解对应的组合预测一定为优性组合预测方法。

组合预测模型(4)目标函数是求最大值,则有
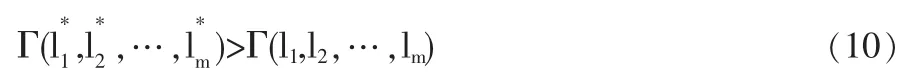
因为组合预测模型(4)的冗余度 k<(m-1)/m,所以最优解中至少有两个非 0 分量,从而(1,0,…,0)T,(0,1,…,0)T,…,(0,0,…,1)T这m个m维单位列向量分别是组合预测模型(4)的可行解而不是最优解,由(7)、(10)式知

3 冗余预测方法的存在性及其判定
定理4组合预测模型(4)的最优目标函数值是的单调不减函数,即
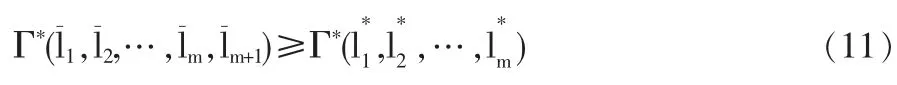
定理4表明在实际过程中组合预测模型(4)再增加一个单项预测方法时,对应的最大的算术平均最小贴近度可能不变,在一定条件下组合预测模型(4)可能存在冗余预测方法。
定理5若组合预测模型的无量纲化指标误差信息矩阵E=(eit)m×N中任一列m个元素e1t,e2t,…,emt的符号完全相同,且第j种单项预测方法严格优超第k种单项预测方法,则组合预测模型(4)的冗余度至少为1/m,即至少存在第种单项预测方法为冗余预测方法。
证明:假设第种单项预测方法不是冗余预测方法,则在组合预测模型(4)的最优解中,第 k种单项预测方法对应的最优权系数
因为E=(eit)m×N中任一列m个元素e1t,e2t,…,emt的符号完全相同,所以从而最优解L*对应的目标函数值为



因为第j种预测方法严格优超第k种预测方法,即|ejt|<|ekt|且 yjt>ykt,所以上式为:

4 实证
为了反映本文提出的新的相关性组合预测模型的有效性,应用基于向量夹角余弦的相关性指标的组合预测模型[6]中的数据进行实证分析,基础数据见表1

表1 指标实际值和各单项预测方法预测值数据
利用LINGO软件计算得组合预测模型 (4)最优权系数为:l1=0.6506,l2=0.3494,l3=0。

表2 指标实际值和基于算术平均最小贴近度的组合预测值
按照组合预测效果评价的原则,采用下列误差指标作为评价指标体系。


表3 各种方法预测效果评价指标体系
从表3可以看出,基于算术平均最小贴近度的组合预测模型的各误差指标均低于三种单项预测模型预测误差指标值,表明提出的组合预测方法能够有效提高预测精度。同时,基于算术平均最小贴近度的组合预测模型的各误差指标与文献[6]中各误差指标结果相当,多数误差指标优于文献[6],因而基于算术平均最小贴近度的新的相关性组合预测模型是一种有效的组合预测方法。
另外三种单项预测方法预测值序列与实际观测值序列的算术平均最小贴近度分别为Γ1=0.7565、Γ2=0.6556和Γ3=0.2558,组合预测值序列与实际观测值序列的算术平均最小贴近度为 Γ=0.7626,满足 Γ>max(Γ1,Γ2,Γ3),故由定义 4 知实例基于算术平均最小贴近度的最优组合预测模型为优性组合预测。
[1]Bates J.M.,Granger C.W.J.Combination of Forecasts[J].Operations Research Quarterly,1969,20(4).
[2]唐小我,马永开,曾勇,杨桂元.现代组合预测和组合投资决策方法及应用研究[M].北京:科学出版社,2003.
[3]陈华友.组合预测方法有效性理论及其应用[M].北京:科学出版社,2008.
[4]唐小我.组合预测误差信息矩阵研究[J].电子科技大学学报,1992,21(4).
[5]王应明.基于相关性的组合预测方法研究[J].预测,2002,21(2).
[6]陈华友,盛昭瀚,刘春林.基于向量夹角余弦的组合预测模型的性质研究[J].管理科学学报,2006,9(2).
[7]杨桂元,唐小我.非负权重组合预测模型优化方法研究[J].数量经济技术经济研究,1998,15(3).
[8]马永开,杨桂元,唐小我.非负权重组合预测的冗余定理[J].系统工程理论与实践,1995,4(4).
[9]刘普寅,吴孟达.模糊理论及其应用[M].长沙:国防科技大学出版社,1998.

