动态测量误差损失函数研究

张月义，宋明顺，韩之俊

（1.中国计量学院 经济与管理学院，杭州 310018；2.南京理工大学 经济管理学院，南京 210094）

0 引言

20世纪60年代末期，Taguchi博士将质量损失函数和他提出的信噪比（SN比）应用到测量领域，逐渐形成一门新的学科《测量质量工程学》[1]。测量质量工程学在评价测量系统的优劣、开发质高价廉的测量系统、选择和配备适宜的测量设备等方面有着广泛的应用。目前，在日本计量领域，以田口为代表的测量质量工程学的思想和技术方法占据着主导地位。在日本计量管理协会，由于通商产业省的大力支持和宣传，极力鼓励和指导工程技术人员在实践中加以应用，现已取得了良好的经济和社会效益。传统评价测量质量优劣的方法是用测量不确定度评定的方法进行的[2][3]，在测量质量工程学领域则用测量特性信噪比和测量误差损失函数来表征测量质量的优劣。但在现有关于测量误差损失函数的文献中[4][5]，都是针对被测量为静态即被测量固定不变的情况，对于动态测量情况下的测量误差损失函数没有研究。本文在研究田口静态测量误差损失函数的基础上，研究了动态测量的测量误差损失函数。在实际的测量系统评价过程中，可能是测量几个标准物质进行的；还可能是在工作现场，工作人员随机抽取几个实物进行测量质量评价。本文将分为上述两种情况进行研究，并给出针对实际问题的应用实例。

1 静态测量误差损失函数

在测量质量工程学中，使用测量误差二次损失函数来表征测量质量。设测量特性的真值为m，其测量结果为y，当y≠m，则造成质量损失，且|y-m|越大，E［L（y）］越大。 设 L（y）在y=m处存在二阶导数，按泰勒级数展开公式有：

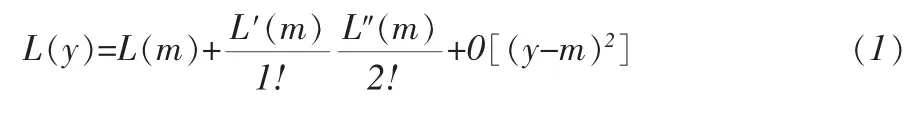
不失一般性，若 y=m 时，L（y）=L（m）=0；又因为 L（y）在y=m时达到极小，故L′（m）=0；再略去二阶以上的高阶项，因此有：

该函数称为测量误差损失函数。对该函数两边求数学期望，则有：

称 E［L（y）］为测量质量水平。

当进行重复测量时，设被测量的真值仍然为m，测量观测值分别为 y1，y2，…，yn，称：

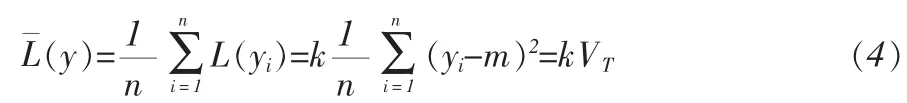
2 动态测量误差损失函数设计

当被测量为动态特性时，其目标值（即被测量真值）随着被测量的变化而变化。设测量结果的测量特性值为y与被测量 M 之间存在线性关系，则有 y～N（α+βM，σ2），即：

其中，M 为被测量，ε～n（0，σ2）。

当被测量变化时，测量结果的动态特性值y会取一系列随机值。对于动态的测量特性，与静态测量误差损失函数不同的是，目标值m不是固定值，而是一个随被测量变化而变化的目标函数，即有：

与静态测量误差损失函数相似，我们定义动态测量误差损失函数为：

这里的损失系数K可以用相同的方法确定，当知道测量特性值与目标值偏离△时的损失为A元时，损失系数K=A/Δ2。但式（7）中的α，β，是未知常数，即使再给出一个被测量M得到一个测量特性值y也无法计算L（Y）。

对式（7）求数学期望，并将式（5）代入得：

简记为：

由此可见，确定动态测量误差平均损失的关键是求出测量误差方差的估计值σ^2。

2.1 测量几个标准物质时动态测量误差损失函数

在实际衡量测量误差大小时，有时是用一些标准物质测量若干次来评价测量质量特性。

设有 k 个标准物质 M1，M2，…，Mk，称 M 为被测量（信号因子），M1，M2，…，Mk为 M 的 k 个水平，对每个标准物质，进行r0次独立重复测量，测量结果如表1所示。

表1 测量结果数据表

在表1中，Ti为标准物质为Mi时重复测量ro次所得测量特性值之和，T表示所有kr0次测量的测量特性值之和。根据最小二乘法原理，测量误差损失函数的确定步骤为：

（1）求 α，β 的估计值

（2）进行波动平方和分解

总波动平方和ST为：

其自由度为：

信号M引起的波动平方和Sβ为：

相应自由度为：

测量误差引起的波动平方和Se为：

2.1 测量几个实物时动态测量误差损失函数

在工作现场有时是测量几个实物来评价测量系统测量质量的。设在工作现场随机抽取k个实物，其未知的真值分别用M1，M2，…，Mk表示，对每个实物进行r0次独立重复测量，测量结果表与表1基本致，只是测量实物时信号因子M未知。此时，Ti为实物Mi时重复测量r0次所得测量特性值之和，T表示所有kr0次测量的测量结果之和。

与测量几个标准物质相比，除了真值未知外，按照最小二乘法原理，只有信号M引起的波动平方和计算公式不同，其他计算过程基本一致。测量几个实物时，实物M引起的波动平方和计算公式为：

（4）求动态测量的测量误差损失函数

对于动态测量误差损失的数学期望可以由式（8）得：

将式（17）代入式（18）得动态测量的测量误差损失函数的估计式为：

相应自由度为：

（3）求测量误差方差的估计值

此时，测量误差引起的波动平方和Se为：

相应自由度为：fe=k（r0-1）

则测量误差方差的估计值为：

于是未知信号因子时测量误差损失函数的估计式为：

3 例证

三坐标测量仪是一种常用测量工具，主要用于测量复杂形状表面轮廓尺寸。为研究某三坐标测量仪的测量性能，工程师选择了五种标准零件：M1=10mm，M2=15mm，M3=20mm，M4=25mm，M5=30mm。每种标准零件测量3次，测量结果如表2所示。

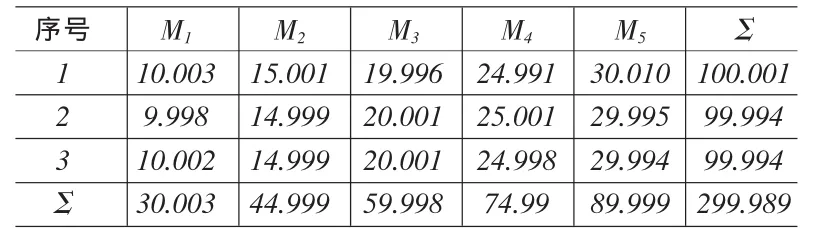
表2 三坐标测量仪测量数据表

设该三坐标测量仪的最大允许误差 （即容差△）为0.020mm，测量误差超出最大允许误差时的损失为20元，试确定该三坐标测量仪的测量误差损失函数。

解：（1）计算 α，β 的估计值

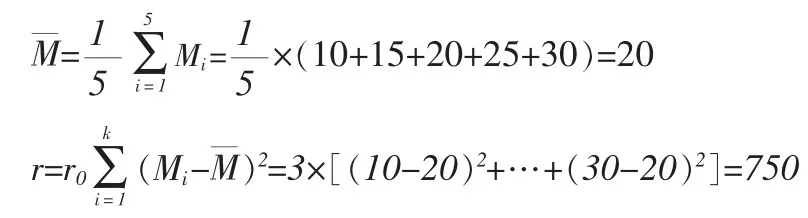
于是：

（2）进行波动平方和分解

总波动平方和ST为：

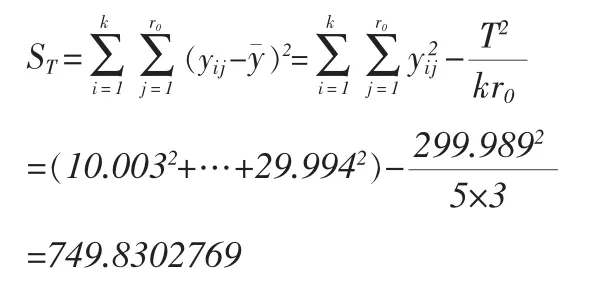
其自由度为：

f总=kr0-1=5×3-1=14

信号M引起的波动平方和Sβ为：

相应自由度为：

fβ=1

测量误差引起的波动平方和Se为：

相应自由度为：

fe=kr0-2=5×3-2=13

（3）求测量误差方差的估计值

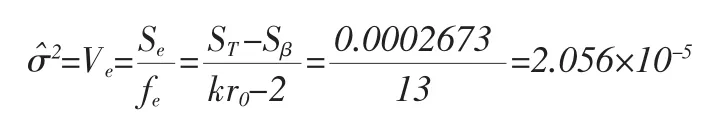
（4）求动态测量的测量误差损失函数

由于Δ=0.02mm，A=20元，则损失函数的系数为K=

由（19）式计算测量误差损失的估计值为：

计算结果表明，上述15次测量的平均测量误差损失为1.028元。

现在假定被测量是工作现场随机抽取的实物进行测量，其余条件和测量结果完全一致。测量误差损失函数的计算步骤中被测量M引起的波动平方和为：

自由度：fM=4

测量误差引起的波动平方和为：

Se=ST-SM=749.8302769-749.8300303=0.0002466

相应自由度为：

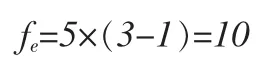
则测量误差方差的估计值为：

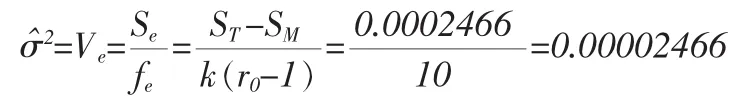
损失系数的确定方法与测量几个标准一致，K=50000。

于是测量几个实物时测量误差损失的估计值为：

计算结果表明，如果我们用实物去测量，造成的损失要比用已知信号因子测量时大些。

4 结束语

传统测量系统分析经常用随机测量误差标准差或测量结果不确定度来表征测量质量的优劣。在田口创建的测量质量工程学理论中，用测量误差损失函数和测量特性的SN比加以描述。但现有的测量误差损失函数只是针对被测量是固定值的情况。实践中被测量往往是动态变化的。本章在研究静态测量误差损失函数的基础上，提出了动态测量误差损失函数，详细介绍了确定动态测量误差损失函数的步骤，包括测量几个标准和测量实物时测量误差损失函数的确定方法，并通过具体实际问题进行了应用举例。

[1]韩之俊，靳京民.测量质量工程学[M].北京:中国计量出版社,2000.

[2]王伟，宋明顺，陈意华等.蒙特卡罗方法在复杂模型测量不确定度评定中的应用[J].仪器仪表学报，2008，29（7）.

[3]Stephen V C,Robert D M.A Two-stage Monte-carlo Approach to the Expression of Uncertainty with Non-linear Measurement Equation and Small Sample Size[J].Metrologia,2006,（43）.

[4]赵宇，陈松涛.用田口方法推断校准仪器的测量不确定度[J].电子测量与仪器学报，2005，19（2）.

[5]薛跃，盛党红，朱立峰等.田口式测量质量工程学与传统MSA的比较分析[J].系统工程理论与实践，2006，（8）.