指数分布场合无失效数据参数的分级Bayes估计

蔡国梁，徐伟卿，赵 树

（江苏大学 理学院，江苏 镇江 212013）

0 引言

随着科技的发展，人们对产品的质量要求不断提高，产品的可靠性也越来越高。，在可靠性试验中，时常会遇到无失效数据(Zero-failure data，即在规定的截尾时间内没有产品失效)。 在高可靠性、小样本问题中，经常会出现无失效数据。特别是对于长寿命的试验样品，由于实际试验条件的限制，更容易产生无失效数据。所以对无失效数据进行可靠性研究，越来越具有理论和实际价值。

近年来，应用和改进Bayes方法研究无失效数据的失效概率方面取得了一些进展。 特别是自Lindley和Smith提出多层先验分布的想法和韩明给出先验分布的构造方法以来，多层Bayes方法在无失效数据可靠性参数估计上取得了一些进展。文献[1].[2]改进了多层Bayese方法进行了E-Bayes方法的研究。 文献[3]在威布尔分布场合下提出了一种对累积失效概率的分级Bayese估计。

本文将分级Bayese估计方法应用于指数分布下的无失效数据的研究。首先用分级Bayes方法对Pi估计；然后引用文献[4]的方法，对参数θ和λ进行最小二乘法的估计；最后得到可靠度的估计。

1 数据模型

从以上的实验过程来看，作如下假定:

（1）t=0 时，产品失效的概率为 0，即 F（0）=P（T≤0）=0。

（2）令 pi=P（T≤ti）=F（ti），因为 0＜t1＜t2＜…＜tm，所以 p1＜p2＜…＜pm，且pi较小。下面讨论，假定产品寿命T服从指数分布时，如何利用先验信息，来估计未知参数θ及作可靠度估计。

其中θ是参数，并且T是均值。

为评定产品的可靠性，随机的选取n个样品进行寿命试验，现将这些产品分成m组，各组样品数分别为n1，n2，…，nm，

2 pi的分级Bayes估计

在（θ1，θ2）上的不完全 Beta 分布可表示为 Beta（θ1，θ2，a，b），其分布密度函数为

其中 θ1＜θ2，a＞0，b＞0，Beta 函数

由于产品的失效概率pi∈（0，1），所以很多人在用Beta方法解决问题时，往往把pi的先验分布取为（0，1）上的均匀分布U（0，1）。但是在无失效情况下，失效概率大的可能性小，失效概率小的可能性大。因此，取均匀分布作为pi的先验分布不太恰当。文献[6]中采用一种新的构造多层先验分布的方法——减函数法，即选取pi的减函数作为pi的先验分布的密度函数之核。它符合在无失效情况下，pi大的可能性小，而pi小的可能性大的要求。本文先估计出p1，然后在不完全 Beta（1，1，b）分布下对 p2进行修正得到，再在不完全Beta下对 p3进行修正得到，依次类推得出 pi的分级Bayes估计

3.1 p1的估计

考虑到Beta密度函数在b越大的情况下，其右侧尾部越细，而从Bayes估计的稳健性角度看，尾部越细的先验分布常使Bayes估计的稳健性差。因此，b应有上界c，其中c为常数。 取 a与 b 的超先验分布为 π（a）=1，π（b）=U（1，c） 时，Beta分布的密度函数是单调减函数pm，符合各失效概率pi较小的可能性大，而较大的可能性小的先验信息。

p1的多层Bayes估计为:

2.2 p2的估计

2.3 p1的估计

以 pi的一级先验分布为，1）上的不完全b）分布作为先验分布，则 pi的先验分布为：πi（pi）=f（pi/c，）则pi的分级Bayes的估计为：

3 参数θ的估计

当产品的寿命T服从指数分布exp（θ）时，产品到时间ti失效的失效概率为：

Pi=P（T≤ti）=1-exp（-λti）（λ=1/θ）（i=1，2，…，m）

又可以表示为：

-ln（1-pi）=λti（i=1，2，…，m）

用p^i代替 pi产生的误差 εi，上式改写为 -ln（1-pi）=ti/θ+εi，i=1，2，…，m。 设-ln（1-pi）=yi，1/θ=λ。 则上式可变形为如下的线性方程 yi=λti+εi。 再设 Y=（y1，y2， …ym）;T=（t1，t2， …，tm）；ε=（ε1，ε2，…，εm），则 Y=λT+ε。

利用最小二乘法可得参数的λ的估计为：

参数θ的估计为

进而可得任意时刻t的可靠度估计为

4 实例

以文献[7]试验数据为例，求出可靠性估计。某产品的可靠性试验中，随机抽取51个样本进行定时截尾试验，整个过程无一样本失效，全部试验数据如下表1所示。其中i是组号，ti是该组的运行时间，si是样品个数。表2给出了可靠度的估计，其中ti是该组的运行时间的整数修正。

通过数据可以看出，随着时间的增加，失效率逐渐降低。从而验证了试验的无失效情况下，失效概率大的可能性小，失效概率小的可能性大的特性。说明本文用分级Bayes方法对指数分布场合下可靠度估计的可行性。

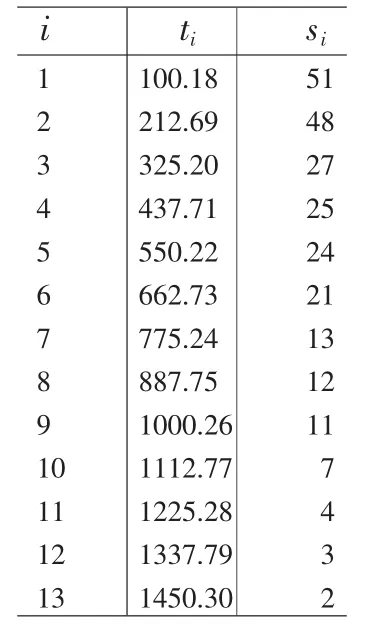
表1 试验数据

5 结论

利用分级Bayes方法，分析了无失效数据在指数分布场合下的失效概率pi，给出了pi的分级Bayes估计。通过修正后的pi，利用最小二乘法估计出可靠度R，通过实例数据，证明了方法在指数分布场合下对失效概率估计的可行性。

[1]Guoliang Cai，Lailin Wu.Bayesian Analysis of Failure Probability UnderZero-failure Dat a[C].ProceedingsofFirstWorld Congress on Global Optimization in Engineering&Science(WCGO-2009)， 2009，（2）.

[2]蔡国梁，吴来林，唐晓芬.双超参数无失效数据的E-Bayes可靠性分析[J].江苏大学学报（自然科学版），2010，31（6）.

[3]刘腾腾，刘健亭.滚动轴承小样本无失效数据的Bayes可靠性分析[J].河南科技大学学报，2009，21（6）.

[4]龙宾.指数分布下无失效数据的参数和可靠度估计[J].乐山师范学院学报，2006，21（5）.

[5]朱宁，方爱秋.不同损失下指数-威布尔参数的Bayes的估计[J].统计与决策，2008，21（4）.

[6]韩明.多层先验分布的构造及其应用[J].运筹学与管理，1997，（6）.

[7]赵海兵，程依明.指数分布场合下无失效数据的统计分析[J].应用概率统计，2004，（2）.