一类保序最优化问题的迭代算法

邓文丽，朱莹莹

（江西师范大学 数学与信息科学学院，南昌 330027）

0 引言

约束条件下的统计推断已经成为统计分析的一个重要领域，保序回归是约束条件下的统计推断的一类典型问题。保序回归的研究从20世纪中叶就已经开始，到20世纪60年代，保序回归得到了广泛的重视。Bartholoremew,Barlow等对此进行了研究，并且于1972年联合出版了保序回归的第一本专著 《The theory and application of Isotonic Regression》，使得保序回归问题得到了进一步的重视和发展，成为热门话题。

在回归分析问题中，假定自变量为 z=（z1，z2，…，zn），因变量为 y=（y1，y2，…，yn）。 在很多情况下，研究者并没有关于回归函数的很多信息，而只是一些关于变量的约束条件，比较典型的一类就是，假设z的元素是经过排序的，z1≤z2≤…≤zn，yi会随着zi递增，这样一种情形被称为保序回归；yi会随着zi递减，被称为逆序回归。两种情况合在一起，被称为单调回归。详细介绍可参见文献 de Leeuw（2005）。

令 x=（x1，x2，…，xn）表示 y 所对应的回归拟合值，保序回归可以表述为：

寻找 x*=（x1*，z2*，…，zn*）∈G，G={x∈Rn|x1≤x2≤…≤xn}使得

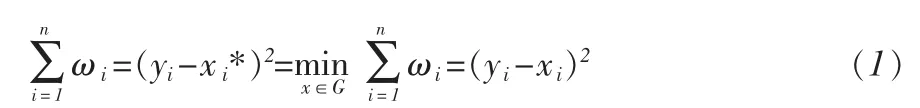
其中 ω=（ω1，ω2，…，ωn），ωi≥0 （i=1，2，…，k）是给定的权数，ω1+ω2+…+ωn=1。这时x*被称为y的保序回归。

保序回归问题的求解过程中，有一个最基本的定理是：如果yi＞yi+1，那么它们对应的拟合值满足x^i=x^i+1。因此，保序回归的求解归结为找到指标集{1，2，…，n}的一个合理划分，B1，B2，…Bk，k≤n，使得 B1+B2+…+Bk={1，2，…，n}，对划分中的任意一块Bj而言，任给i∈Bj，xi都是相等的，在满足这样条件的划分中，寻找（1）的解。 Ayer et al.（1995）提出的 PAVA（Pool Adjecent Violators Algorithm）算法使问题（1）从理论上得到了很好的解决。PAVA算法求得的“最优”划分B1，B2，…Bk，k≤n，对划分中的任意一块 Bj而言，任给 i∈Jj，。

本文将经典的保序回归问题拓展到绝对损失下，去解决下面的最优化问题：

寻找 x*∈G，G={x∈Rn|x1≤x2≤…≤xn}使得

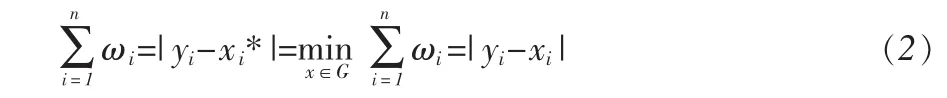
其中 ω=（ω1，ω2，…，ωn），ωi≥0 （i=1，2，…，k）是给定的权数，ω1+ω2+…+ωn=1。

本文将根据PAVA思想过程给出一种迭代算法，通过迭代过程分析得出最优化问题（2）的解，并给予证明。

1 利用迭代算法求解最优化问题

J=（B1，B2，…，Bk），B1，B2，…，Bk，k≤n 是指标集{1，2，…，n}的一个划分。 若 B={p，p+1，…，q}，1≤p≤q≤n，J中包含 p-1的元素，用B-表示；包含q+1的元素用B+表示。若p=1时，B-=φ，若 q=n 时，则 B+=φ。 用［AM（B）L，AM（B）U］记指标集 B所对应y的元素的加权中位数所在集合，有

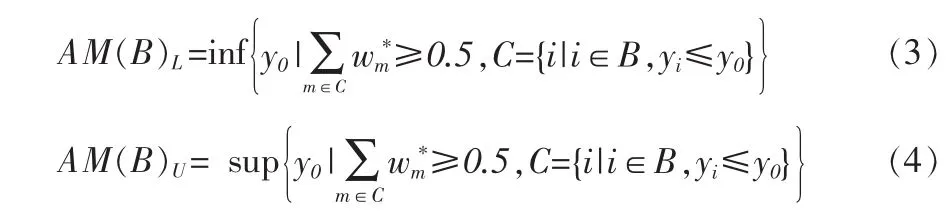
类似PAVA算法的思想，下面针对本文讨论的最优化问题（2）给出一种迭代算法。

G 表示可行域{x1，x2，…，xn|x1≤x2≤…≤xn}，如果（y1，y2，…，yn）∈G，则=yi，i=1，2，…，n 否则，令 J={{1}，{2}，…，{n}}，B={1}，进入迭代算法。

（1）若 B+=φ，则迭代结束，xi*∈［AM（B）L，AM（B）U］，i∈B，B∈J；否则将 AM（B）L，AM（B）U和 AM（B+）L，AM（B+）U进行比较。

若 AM（B）U≤AM（B+）L，B=B，回到初始；

若 AM（B）U＞AM（B+）L，但 AM（B）L≤AM（B+）U，即

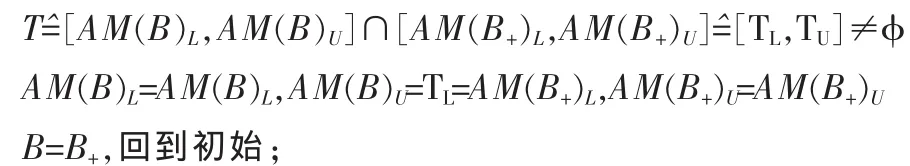
若 AM（B）L＞AM（B+）U进入第（2）步。

（2）J=J{B，B+}∪（B∪B+），令 B=B∪B+，计算AM（B）L=AM（B）U。

（3）若 B-=φ，进入第（1）步；否则进行下面的判断：

若 AM（B-）U≤AM（B）L，回到第（1）步；

若 AM（B-）U＞AM（B）L，但 AM（B-）L≤AM（B）U，即

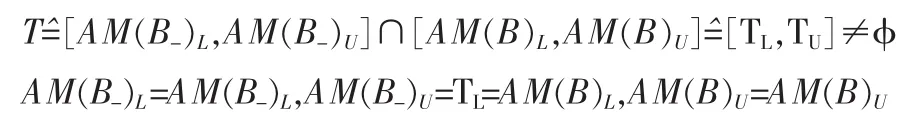
进入第（1）步。

AM（B-）L＞AM（B）U，进入第（4）步；

（4）J=J{B，B-}∪（B∪B-），B=B∪B+，进入第（3）步。

迭代的结果，指标集{1，2，…，n}被划分成了 B1，B2，…，Bk，k≤n 是指标集的一个划分。 B1+B2+…+Bk={1，2，…，n}，而且最优解属于集合

下面证明（5）所表示的就是最优化问题（2）的解集。

2 最优解的相关证明

定理 1 假定指标集 B=（p，p+1，…，q），∀i∈B，yi∈R，yi所对应的权数记为 wi，yp≥yp+1≥…≥yq。 数列{yi，i∈B}的加权中位数所在的集合表示为［AM（B）L，AM（B）U］，［AM（B）L，AM（B）U］如（3）、（4）所示，那么

①使得

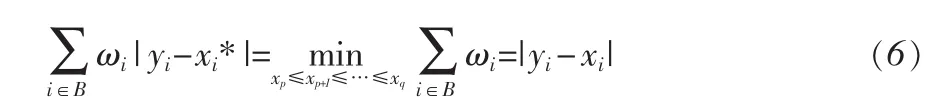
定理 2 若 B=（p，p+1， …，q），1≤p≤q≤n 任给 p≤i≤+1≥yi+2≥…≥yq，记

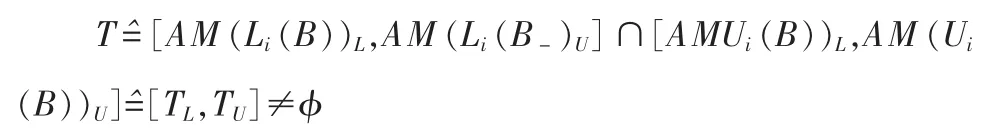
①若 T≠φ，选取

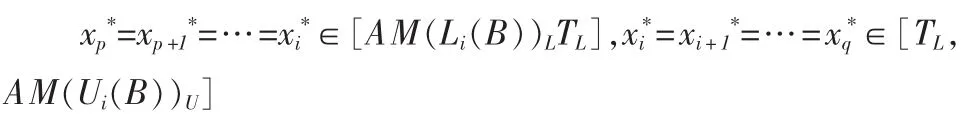
可使得

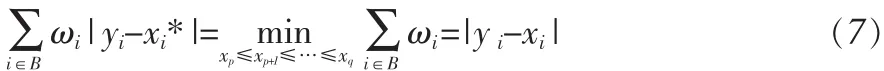
证明：①式显然成立，下面证②。

根据定理1中的结论①，又因为yp≥yp+1≥…≥yi，yi+1≥yi+2≥…≥yq， 那么使得成立的一定满足使得成立的一定满足…=。 所以使得（7）式成立的满足

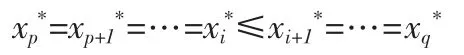
因为 T=φ，即 AM（Ui（B））U＜AM（Li（B））L，显然使得（7）式成立的{，i∈B}还应满足

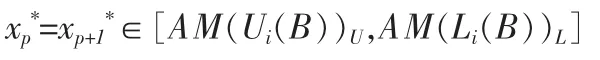
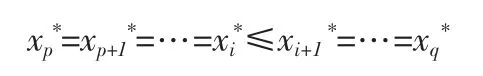
定理 3 若 B={p，p+1，…q}，1≤p≤q≤n，任给 p≤i≤q，Li（B）{p，p+1，…，i}。 记记

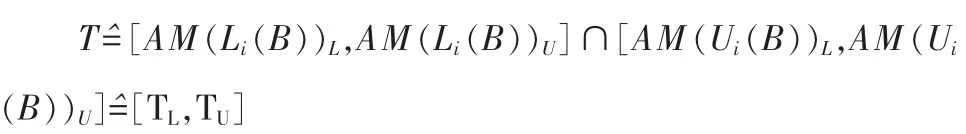
①若T≠φ，选取

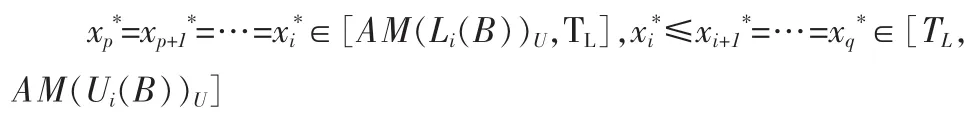
可使得

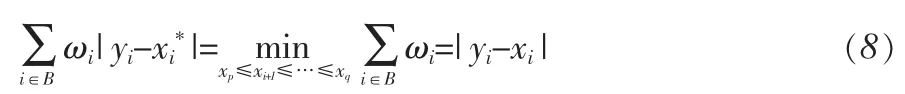
例：已知 y1=4，y2=5，y3=1，y4=6，y5=8，y6=7 并且 wi=1/6，i=1，…，6。 求 x* 使在满足 x1≤x2≤…≤x6的限制下达到最小。

解：y1=4＜y2=5，y2=5＞y3=1，所以 B1={1}，B2={2，3}

取 AM（B1）L=AM（B1）U=4，AM（B2）L=AM（B2）U=5，由此重新记 AM（B1）L=AM（B1）U=4，AM（B2）L=4，AM（B2）U=5；AM（B2）U＜y4＜y5；而 y5＞y6，所以 B3={4}，AM（B3）L=AM（B4）U=6；B4={5，6}，AM（B4）L=AM（B4）U=8，显然 AM（B4）L＞AM（B3）U=6。 所以选取，J={{1}，{2，3}，{4}，{5，6}}［4，5］，∈［7，8］，

用上述迭代计算该模型的解的次数为O（n），当n不是很大时，其运算并不复杂，当n很大时，利用计算机辅助仍然可以比较快得出结果。因此，加权最小绝对偏差在保序限制下迭代计算仍是比较实用的，有奇异值出现时，其所得解也比加权最小平方损失下的解更稳健。

[1]Michael J BEST，Nilotpal Chakravarti.Active Set Algorithms for Isotonic Regression;A Unifying Framework[J].Mathematical Programming，1990，（47）.

[2]De Leeuw，Jan，Hornik，Kurt，Mair，Patrick.Isotone Optimization in R:Pool-Adjacent-Violators Algorithm （PAVA） and Active Set Methods[M].UC Los Angeles:Department of Statistics，2009.

[3]De Leeuw.Monotonic Regression，Encyclopedia of Statistic in Behavioral Science[M].New York:Wiely，2005.

[4]史宁中.保序回归与最大似然估计[J].应用概率统计，1993，（19）.

[5]刑务强.保序回归的研究及应用[D].西北工业大学，2002.

[6]赵选民，刑务强.凸规划下的保序回归[J].数理统计与管理，2003，（22）.