一般抽样设计下的随机化调查技术

赖俊峰，闫在在，邴淑琴

（内蒙古工业大学 理学院，呼和浩特 010051）

0 引言

近年来，随机化调查方法研究不论从抽样设计还是估计量的构造，都开始深入到复杂抽样调查中。主要包括Jong-Min Kim等人[9～12]讨论了分层抽样下属性特征随机化调查理论与方法；Shaul K.等[13]中利用二级连续抽样方案改进了Warner RRT；Horng-Jinh Chang讨论了利用两个独立的子样本同时顾及敏感属性比例.虽然关于随机化调查的研究有很多，但是这一方面研究还远不够全面和系统,主要体现在这些调查方法没有统一的评价标准并且与抽样设计有关。在随机化调查中，关于属性特征和数量特征许多具体方法，其方法中抽样设计多见于SRSWR,SRSWOR,PPS等方案[1]。2006年Raghunath Arnab[7]研究了上述问题。本文将提出一个一般化的估计量并给出期望和方差，拟初步建立在任意抽样设计p（s）（s为样本）下数量特征和属性特征敏感问题的统一的随机化理论。

1 定义与记号

用大写字母与小写字母分别表示有关总体与样本的量，ER、VR代表对随机化装置求期望和方差，EP、VP代表对抽样设计求期望和方差。从一个容量为N的总体中抽样两个互相独立的容量分别为n1，n2的样本s。NG（未知）表示总体中拥有敏感问题的数量，p（s）表示样本s出现的概率，设π表示总体中敏感问题X所占的比例。

定义1在不放回不等概率抽样中，总体中每个单元i被包含到样本的概率记作 Pr（i）=πi，任意两个单元 i，j都包含到样本的概率称为包含概率 Pr（i，j）=πij（inclusion Probabilities）。

容易证明[8]对固定的样本容量n包含概率πi具有性质：

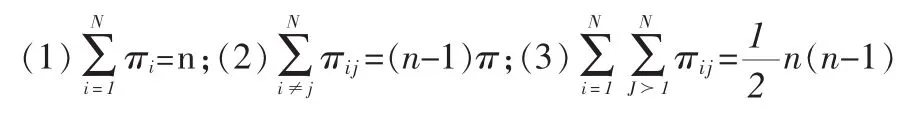
二步抽样下列两式成立：

2 一般随机化回答技术

调查者从容量N的总体中以概率p（sk）抽取容量为nk样本sk（k=1，2），第i个回答者若有敏感属性则他回答敏感属性值xi，否则它将通过一个随机化装置回答一个概率分布已知的随机值Rki。这个随机化回答装置可以是一个纸片或其它,回答者通过随机抽出一个数Rki。则在样本Sk（k=1，2）中第i个回答者回答值Zki如下：

设θk，代表随机化装置Rk的均值和方差 （已知），γ（k）代表回答值的均值，则有=ER（Zki），令

则

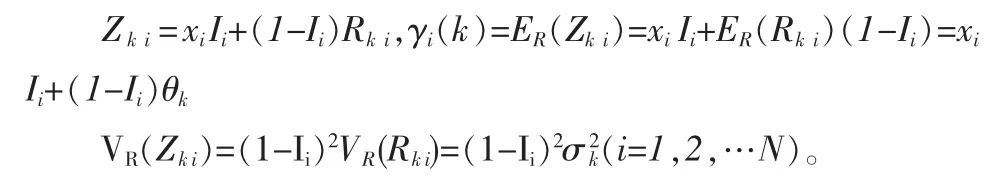
下面给出所定义TK的期望和方差性质：

定理 1 TK的数学期望 E（TK）=πμx+（1-π）θk。

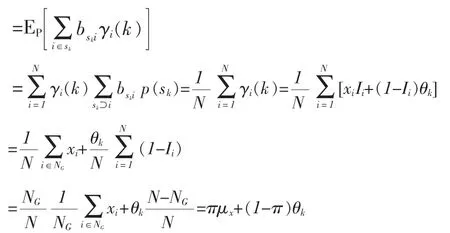
定理2 TK的方差

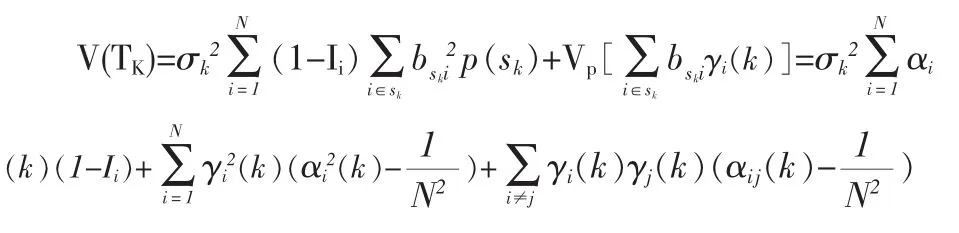
其中：

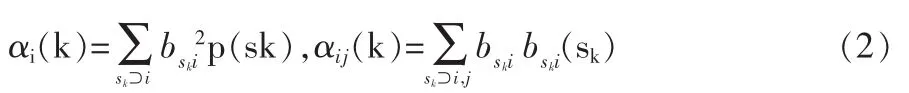
证明：

定理 3 V（TK）一个无偏估计量其中

证明：

3 估计量讨论

敏感性问题调查从统计上看可以分成两类，一类是属性特征敏感问题调查，解决的是估计总体中各种比例；另一类是数量特征敏感问题调查，解决的是估计总体某项指标的均值或总值[2]。对于属性敏感问题我们所关心的是具有敏感属性的人在总体中所占的比例π=NG/N，而对于数量敏感问题我们关心的是具有敏感属性的多少根据估计量

（1），得出如下定理：

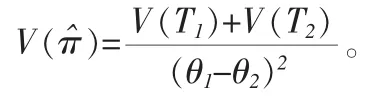
证明：定理5属性敏感问题的无偏估计量的方差为：推论1属性敏感问题π的无偏估计量π^的方差估计为：定理6对于数量特征敏感问题均值μ的估计量：

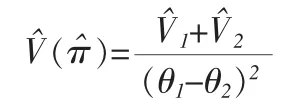
证明：

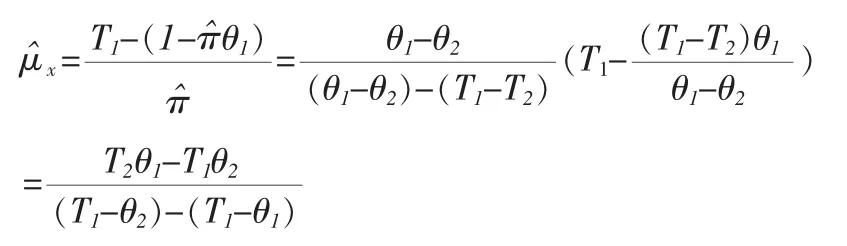
4 一些特殊的抽样方案

4.1 简单随机不放回抽样

对于简单随机不放回抽样（STSWOR）[3]设计中，从样本容量为中抽取样本量为的样本包含概率πi=n/N，πij=n（n-1）/N（N-1）取 bsi=1/nk,则

（2）TWOR的方差变为：

（3）属性敏感问题的比例的无偏估计：

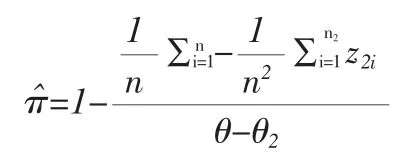
（4）数量特征敏感问题均值μx估计量的估计量：

4.2 Horvitz-Thomson估计量

在不放回不等概率抽样πi是第i单元的包含概率。Horvitz与Thompson在1952年提出了Horvitz-Thompson估计量[6]，取 bsi=1/Nπi（k），则

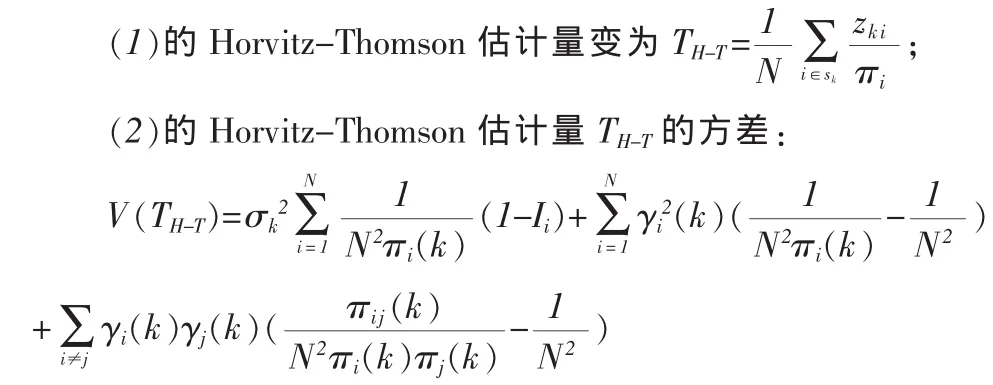
（3）属性敏感问题的Horvitz-Thomson估计量的无偏估计：

（4）数量特征敏感问题的Horvitz-Thomson均值估计量：

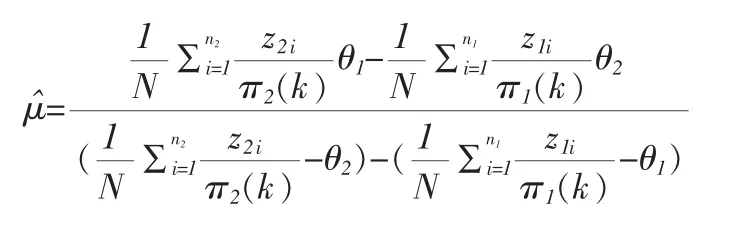
5 结论

由上述证明可知本文所建立的方法搭起了属性特征和数量特征RR调查的理论的联系，抽样设计也是一般的，因此这是一个非常一般化的RR调查方法。

[1]赖俊峰，闫在在等.沃纳模型在社会问卷调查中的应用及改进[J].统计与决策，2010，（8）.

[2]Anthony Y.C.Kuk.Asking Sensitive Questions Indirectly[J].Biometrika,1990,77(2).

[3]闫在在，聂赞坎.随机化技术的公平比较[J].数学物理学报，2004，24(A)(3).

[4]范金城，闫在在.多元抽样技术（Ⅰ）[J].工程数学学报,1998，15（4）.

[5]闫在在，聂赞坎.严格πps抽样方案在不放回不等概率抽样中的可容许性[J]. 数学物理学报，2002，22（4）.

[6]Horvitz,D.G.,Shah,B.V.,Simmons,W.R..The Unrelated Question Randomized Response Model[J].Journal of the American Statistical Assoc.,1969,64（326）.

[7]Raughnath,Georg.Dorffner.Randomized Response Technique for Complex Survey Designs[J].Statistical Papers,2006,（48）.

[8]冯士雍，施锡铨，抽样调查——理论，方法和实践[M].上海:上海科学技术出版社，1994.

[9]Jong-Min Kim， William D.Warde.A Stratified Warner’s Randomized Response Model[J].Journal of Statistical Planning and Inference，2004，（120）.

[10]Jong-Min Kim，M.E.Elam.A Two-Stage Stratified Warner’s Randomized Response ModelUsing OptimalAllocation[J].Metrika，2005，（61）.

[11]Jong-Min Kim，Matthew E.Elam.Comparison and Analysis of Stratified Randomized Response Models[C].2003Joint Statistical Meetings-Section on Survey Research Methods，2003.

[12]Tasos C，Christofides.Randomized Response in Stratified Sampling.[J].Journal of Statistical Planning and Inference，2005，（128）.

[13]Shaul K.Bar-Lev,Elizabeta Bobovich,Benzion Boukai.A Two-StageSequentialSamplingSchemeforWarner’sRandomized Response Model[J].Communications in Statistics Theory and Methods，2003，（12）.