异方差混合转移分布模型的谱分析
朱文刚,杨芝艳
(南京工程学院 基础部,南京 211167)
0 引言
平稳过程{yt,t=0,±1,…}的谱表示本质上是将{yt}分解为互不相关随机系数正弦分量之和。与平稳过程{yt}的谱分解相应的是其自协方差函数也可以分解为正弦分量之和。确定性函数的Fourier表示是与平稳过程谱分解类似而又为读者更为熟悉的内容。时间序列的“频域”分析就是以这两类谱表示为工具对平稳序列进行分析。基于自协方差函数时间序列的“时域”分析为研究时间序列提供了另一种方法,但频域分析方法往往对某些实际应用更具有启发性,所以我们有必要研究时间序列的频域。近年来,相关工作被国内外众多的学者广泛的研究[1~6],本文将讨论的异方差混合转移分布模型谱分析由于其序列之间的显式表达式在一般情况下是非线性的,故其谱密度通过定义难以获得,所以笔者拟采取基于Herglotz定理的思想求谱密度。
1 模型引入
Berchtold(2003)引入的K个成分的异方差混合转移分布模型定义如下:
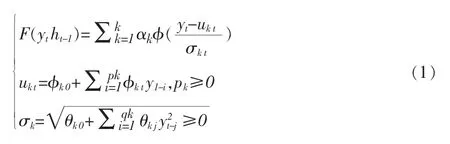
记作 F(yt|h-1)~HMTD(k;p1,…qk)。 这里 F(yt|ht-1)是给定历史ht-1的条件下jh,yt的条件分布函数,ht是至时刻 t时的所有信息。Φ(·)是标准正态分布的分布函数,αk表示第k个成份的权重,满足
2 主要公式的推导及定理的证明
引理1[11]设k阶线性差分方程

其中 α1, …,αk是实数,αk≠0,T 是端点为整数的子区间。 上述方程简记为:A(β)ht=0。 其中 A(β)=1+α1β+…+αkβk,β为推移算子。 (2)的通解为:

其中 CIn由初始条件 h0,h1,…,hk-1决定,ξl-t,l=1,2,…,j是 A(z)=1+α1z+…+αkzk的相异零点,rl是 ξl的重数。

其中:μkt=φk0+φk1yt-1+…φkpkyt-pk
证明:作变换 x=(yt-ukt)/σkt,我们有
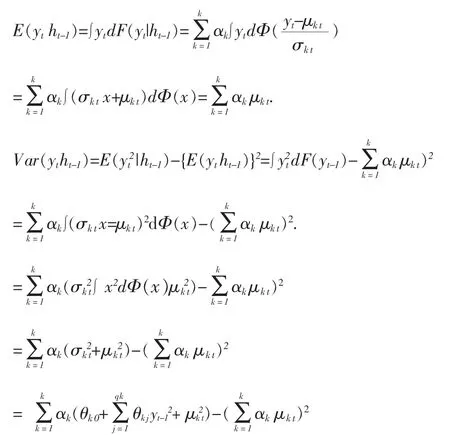
证毕。
假定序列是平稳的,且不妨设 E(yt)=0,则 φk0=0。 又由于Andre Berchtold等人所做的是参数估计,而这里做的是谱分析,不存在过度拟合的问题,所以我们可以对阶进行统一处理。 令 p=max(p1,p2,…,pk),q=max(q1,q2,…,pk)所以模型(1)便转化为模型:
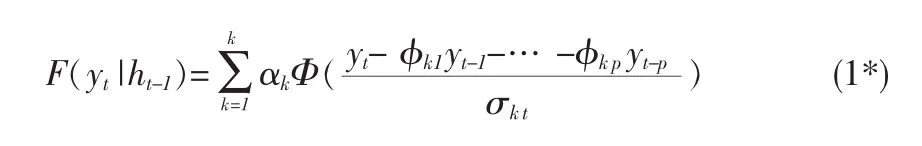
对某些不足p阶的成分令其后面一些回归系数为零即可。
定理1在模型(1*)下,其自协方差函数的递推公式为:
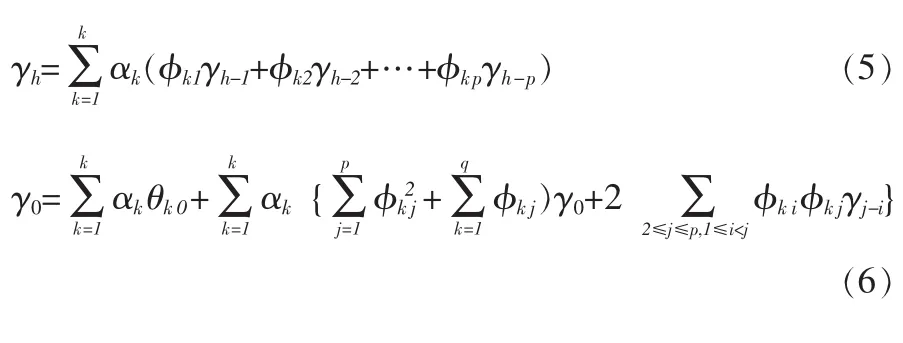
其中:γ-h=γh
证明:令 h>0,则
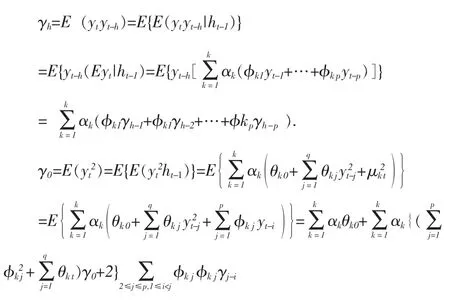
证毕。
引理3[11](Horglotz)定义在整数集上的复值函数是非负定函数的充分必要条件是对任何h=0,±1,…,有(λ),其中 F(.)是(π,-π)上的右连续非降有界函数,F (-π)=0.称函数 F 为 γ(.)的谱分布函数,进而如果dv,则称 f为 γ(.)的谱密度。
引理4[11]定义在整数集上的复值函数 γ(.)是一平稳过程{yt,t=0,±1,…}的自协方差函数的充分必要条件是对任何h=0,±1,…,有其中F是右连续、非降、[-π,π]上的有界函数,F(-π)=0。
引理5[11]定义在整数集上的绝对可和的复值函数γ(.)是一平稳过程 {yt,t=0,±1,…}的自协方差函数的充分必要条件是:对任何 λ∈[π,-π],有f(λ)其中 f是 γ(.)的谱密度。
若我们能从上述定理中的递推公式中解出,并对它辅以绝对可和,即的约束,则我们可以由引理5得到
一般来说,这种表达式不能通过一步获得,从而我们提出“三步算法”,在讲三步算法之前,我们首先对(5)、(6)式按次序重新整理。 由(5)、(6)式得到:
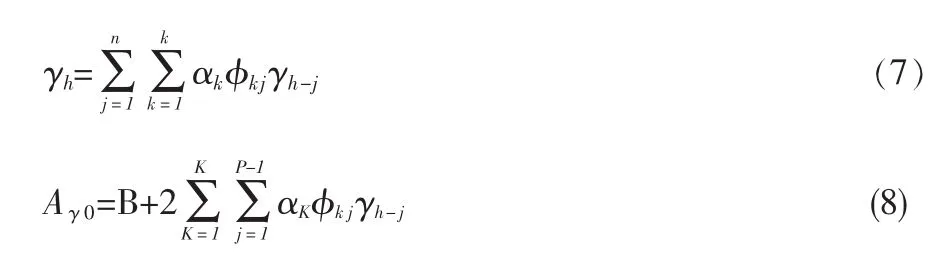

三步算法:
第一步:在(7)式中分别令 h=1,2,…p-1 得到 p-1个方程,这些方程联立(8)可得p个方程组成的线性方程组,从这个线性方程组中可求得初始条件:γ0,γ1,…γp-1。
第二步:差分方程(7)式所对应的特征方程为:
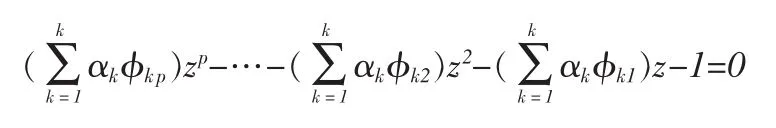
可以求得其 p 个根 ξ1,ξ2…ξp,重根按重数计算.结合初始条件由引理1可得
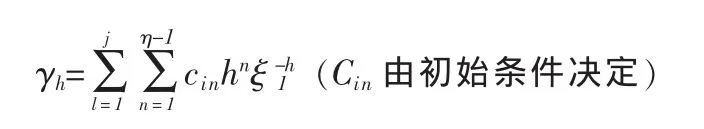
第三步:代入公式
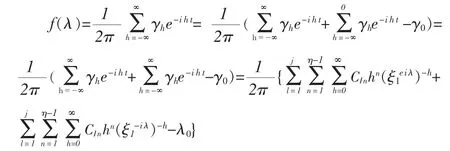

h=0
下面我们针对几种特殊的情形来导出谱密度的具体表达式。
情形 1:若 k=1,p=q=1。
第一步:递推公式为

第二步:差分方程(9)所对应的特征方程为1-φ11z=0,其根为 ξ=1/φ11(单根)。
所以 γh=C10ξ-h其中 C10由初始条件决定.令 h=0 得 γ0=,所以
第三步:计算的表达式

情形 2:若 k=K,p=q=1。
同上,可计算出

其中:A=α1φ11+α2φ21+…+αkφk1,
一般来说,平稳序列的自协方差函数只满足引理(4)的结论,为了使它也满足引理(5)的结论,即要求(11)式也成立的话,还必须要求γh绝对可和,即要求即要求 2即要求

这两式显然成立,因为它们恰好对应模型一阶、二阶平稳条件,
从上可以看出:(1)在这种特定的情况下,模型若是宽平稳(即:一阶、二阶平稳的,则自协方差函数必定是绝对可和的,则谱密度函数必然存在;(2)混合模型中的某些成分可以是单位根过程(非平稳的),但它们的混合可以是平稳的;(3)当k=1时,将回到第(1)种情形;(4)金融时间序列中,有许多模型服从单位根过程,当然混合了单位根过程的混合模型也必然有其实际背景[8]。
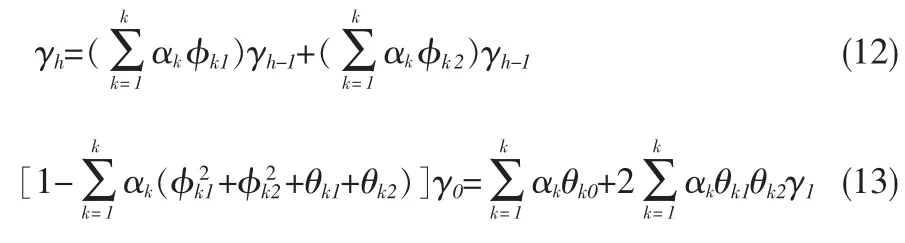
代入(13)式得

则(14)式变为:

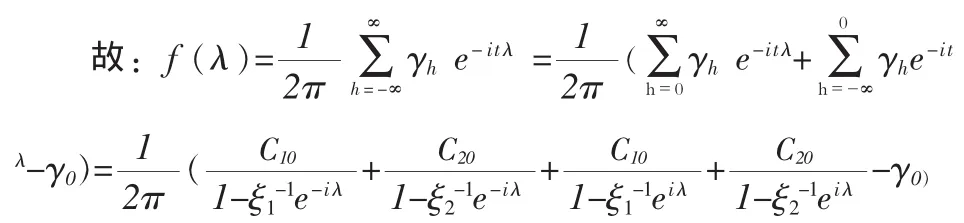
若 A2+4B=0,则 ξ1=ξ2(重根)。
所以此时可设通解为:γh=C10ξ1-h+C11ξ1-h=(C10+C11h)ξ1-h。 由初始条件 γ0,γ1知:C10=γ0,C11=γ1ξ1-γ0。所以:γh=[γ0+h(γ1ξ1-γ0)]ξ1-,从而


3 结论
本文已讨论了一类新的时间序列(HMTD)模型的谱分析问题,这类模型是MAR(mixture autoregressive)模型[2]的推广,而MAR模型又是AR(autoregressive)模型的推广,考虑实际问题的复杂性,对它的谱分析不仅有理论上的价值,而且有实际上的需要。
[1]Le,N.D.,R.D.Martin,A.E.Raftery.Modeling Flat Stretches[J].Bursts,and Outliers in Time Series Using Mixture Transition Distri Bution Models,1996,(91),
[2]Wong,C.S.,W.K.Li.On a Mixture Autoregressive Model[J].J.Roy.Statist.Soc.B,2000,(62).
[3]Chun Shan Wong,Wai Keung Li.On a Mixture Autoregressive Conditional Heteroscedastic Model[J].Journal of the American Statistical Association,2001,(96).
[4]Benes V E.Existence of Finite Invariant Measures for Markov Processes[C].Proceedings of the American Mathematical Society,1967,(18).
[5]Anindya Roy,WayneA.Fuller,YanYan Zhou.A Likelihood Based Estimator for Vector Autoregressive Processes Statistical Methodology,2009,6(3)
[6]田铮,吴雅琴,王红军.非线性时间序列建模的混GARCH方法[J].系统仿真学报,2005,17(8).
[7]刘成瑞.相关系数平稳序列分析方法及其应用[D].北京航空航天大学,2006.
[8]陆懋祖.高等时间序列经济计量学[M].上海:上海科学技术出版社,1998.
[9]Wu,C.F.J.On the Convergence Properties of the EM Algorithm[R].The Annals of Statistics,1983,(11).
[10]Tong,H.Non-linear Time Series[M].New York:Oxford Univer Sity Press,1990.
[11]布洛克威尔.时间序列的理论和方法[M].田铮译.北京:高等教育出版社,2001.

