列车运行图布线方法研究

贾晓秋，关晓宇

（1.西南交通大学 交通运输与物流学院，四川 成都 610031；2.西南交通大学 材料科学与工程学院，四川 成都 610031）

目前，国内外学者在计算机铺画列车运行图方面进行了深入研究，主要涉及单线、双线、区域和网络范围[1-4]。随着我国高速铁路的建设，针对列车运行图的铺画，在有关研究的基础上，设计了基于运行线分解的列车运行图布线方法。该方法可以适应周期或非周期列车运行图的铺画，并在实际规划过程中，能较快地给出较优铺画方案。

1 列车运行图的布线条件及冲突解决方法

列车运行图是列车的开行计划，其前提条件是已经编制好列车开行方案。因此，可以根据列车开行方案确定所规划区段上各区间的列车数量、速度、类型、起停车附加时分、区间纯运行时间、在各车站的停站方案等信息，同时还必须已知车站及区间的各种安全间隔时间、线路长度、到发线数量、容车类型等信息，这些信息是铺画列车运行图的基本信息。

在不考虑安全间隔时间约束的理想条件下，列车运行图的布线问题就是一个简单的列车发到的时间传播过程。为了解决运行线冲突，需要将每一始发站至终到站的运行线分解成若干个列车-区间，假设全部列车的所有运行区间集合构成了的待规划集合TS＝{(ti，sj) |ti∈Tr，sj∈ρti，j＜kti}，如图1所示，最左边的下行列车t，可以按照所经过的区间将其分为3个列车-区间。图1中待规划的列车共有3列，因而共有9个列车-区间，其中TS＝{(t,1)，…，(t,3)，(r,1)，…，(r,3)，(p,1)，…，(p,3)}。

图 1 列车运行线按区间分解示意图

在实际布线过程中，需要动态地考虑运行线之间的冲突问题。对于某一区间，当前待布置的运行线必须满足该区间内已经布置列车到发时间的运行线之间的安全间隔时间约束。若当前待布置的运行线与区间内已布置列车到发时间的运行线发生冲突时，由于已布置运行线的列车区间发到时刻不宜改动，因而具有较高的优先权，所以需要延迟当前待布置运行线的列车区间发车时刻，以缓解冲突，实现列车安全运行。重复上述的布线过程，直至待规划的运行线任务集合为空集，即完成一个运行图的布线任务。

对于同向列车布线，如图2所示，假设当前待规划列车为t，其中p、q、r、m、n是已经布置到当前区间s的运行线，假设τ是t在区间s的初始发车时刻，α、β、γ为该区间列车t的发车位置。

（1）当t在初始位置发车时，会因为列车速度差而与运行线r在区间发生冲突；当t在位置α发车时，可能会因为在车站v不满足运行线间的最小到达间隔约束而与列车p或q发生冲突。

（2）当t在位置β发车时，可能会因为在车站u不满足运行线间的最小发车间隔约束而与列车q或m发生冲突。

（3）只有当列车在位置γ发车时，既满足在车站u的最小发车间隔时间和在车站v的到达间隔时间约束，同时又不会因为列车速度差而导致运行线间的冲突，因而运行线t需要延迟到γ发车。

图 2 布置同向列车时，搜索发车位置示意图

从上述过程看，在区间s＝(u，v) 上布置列车运行线t时，必须考虑已经布置的列车运行线p、q、r、m、n，当发生冲突时，需要延迟待布置列车运行线的发车时刻。因此，列车合理发车时刻的搜索过程就变成在该区间上寻找已布置相邻列车运行线间的“合理时间间隔”问题。

在上述过程中，需要指出的是，若待规划的列车运行线t在车站u计划发车状态是通过车站，而假设t此时又必须在车站u等待前行列车p、q或m离开车站u，并满足一定间隔时间后才能在位置发车，从而不发生冲突，因此列车t在车站u必须将原来计划的通过状态改为停站状态，即技术停站状态。这时列车t在车站u和车站v的发到时刻，均需要增加适当的起停车附加时分，以适应列车技术停站的需要。

对于异向列车布线而言，仅需要在上述搜索列车发车位置时，考虑异向列车之间的车站到发间隔及区间运行时间即可，如图3所示。

图 3 布置异向列车时，搜索发车位置示意图

具体对于周期为T的列车运行图情况，如图4所示，首先需要对已经布置到区间u→v的运行线按照列车发车时间由小到大顺序排列，得到已布置时间的列车运行线序列L＝(y，…，r－1，r，r＋1，…，x－1，x)。在序列L中，为了寻找t的合理发车位置，首先初始化t的最早发车时间：＝＋＋Tp，其中、、、p分别为列车t在车站u的出发时间、到达时间、停站时间 (计划停站或技术停站) 和到发事件之间的模参数，并且进行下列步骤的运行线发车位置搜索过程。

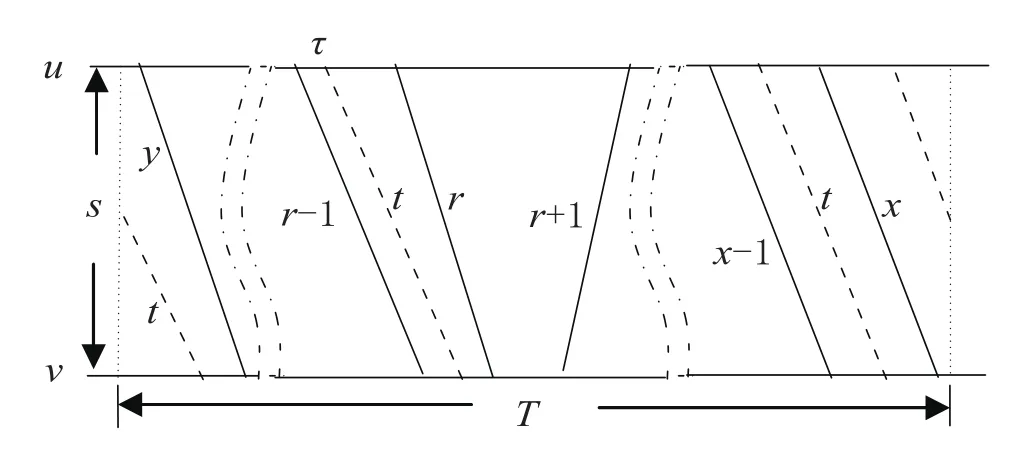
图 4 某区间周期运行图搜索发车位置示意图

步骤 1：假设得到的初始发车位置k位于序列L中的运行线r－1 与运行线r之间。

步骤 2：开始的搜索方向是从位置k向序列L的右方向进行，搜索任意两条运行线间的发车位置，判断该位置是否满足周期情况下的发车约束条件，若满足则停止搜索，置该位置的发车时刻为列车t的发车时刻，否则一直搜索至序列L的最后一个相邻运行线x－1 与x之间的发车位置。

步骤 3：若经过步骤2后，并未得到合理的发车位置，则可以检查L的最后一条运行线x与L最左边的第一条运行线y之间的位置，来判断是否满足周期约束条件；若满足，则置该位置的发车时刻为列车t的发车时刻，并停止搜索过程。

步骤 4：若经过步骤3后，仍未得到合理的发车位置，则需要由序列L中的y与y＋1 位置开始继续向右搜索，直至列车t的初始发车位置的前一个位置，即r－2 和r－1 之间的位置为止。若搜索到可行的发车位置，则将其对应的时刻设置为列车t的发车时刻，并停止搜索过程。

步骤 5：若经过上述搜索步骤仍未得到可行的发车位置，则需要向前回朔。这说明至少列车t在当前运行线铺画图谱下，在区间内无可行解，需重新布置铺画图谱。

非周期列车运行图与周期列车运行图区间发车位置的具体搜索过程类似，可以将该区间上一昼夜的运行线看作是“一个周期”，即只需要令周期T＝1 440 即可。上述区间列车发车位置搜索过程，适用于周期与非周期、单线与双线系统。例如，当搜索单线列车运行的约束条件时，就得到单线列车运行图。

2 列车-区间动态布线搜索树

为了得到满足列车运行图条件的列车-区间集合TS的元素排序，获得列车占用区间的顺序，需要动态地维护一棵搜索树。该树的各个节点表示列车—区间节点 (ti，sj)。在开始时，令该搜索树的根节点为空，表示开始搜索。当获得所有列车-区间节点(ti，sj)的发到时刻后，便可以结束搜索过程。每次在TS中搜索尚未安排列车到发时刻的节点(ti，sj)，一旦得到合适的发车位置，就将合适的列车发到时刻布置到当前的 (ti，sj)，并从TS中删除当前节点 (ti，sj)。反复进行上述搜索直到TS的全部元素均已分配列车发到时刻为止。

设 (ti，sj) 属于搜索树的第l层，则节点 (ti，sj) 的后继节点是TS中所有未布置列车发到时刻的(ti，sj) 节点，即第l层中 (ti，sj) 的兄弟节点和节点(ti，sj+1)。列车运行图的规划过程，实质是在动态搜索树上，寻找一条由初始节点出发至结束节点的路径，按照这条路径可以得到较好的运行图铺画方案。

3 数值算例

某区段列车开行方案如图5所示，列车速度为300 km/h，计划停站时间窗[2，5]60，车站各类间隔时间均为 3 min，列车起停车附加时分为 1 min。用C++实现上述算法，经过 2 000 次迭代计算。列车在各站的一个周期 (1 h) 的到发时刻如表1所示 (一个周期内的数据)。

该算法能在较短时间内解决一个周期内，以及相邻周期之间的列车运行线的冲突问题，而且对周期与非周期列车运行图均适用，对于中小规模的列车运行图实例收敛速度也较快。

图 5 某区段列车开行方案

表 1 某区段列车时刻表

[1] Lindner，T. Train Schedule Optimization in Public Rail Transport[D]. TU Braunschweig，Germany，2000.

[2] Odijk，M. Railway Timetable Generation[D]. TU Delft，The Netherlands，1997.

[3] Peeters L. Cyclic railway timetable optimization[D]. Erasmus Institute，Erasmus University，Rotterdam，2003.

[4] Liebchen C. Symmetry for periodic railway timetables[J].Electronic Notes in Theoretical Computer Science，2004(92)：34-51.