基于胰腺超声内镜图像多尺度分块的分类研究

吴仪俊 余建国 刘岩 金震东

另一方面,随着放射性粒子生产技术的改进、计算机技术的发展,以及放射性物理学、肿瘤学和放射生物学的研究进展,恶性肿瘤的放射治疗已成为临床上的主要手段之一。125I放射粒子肿瘤内植入术是治疗不能手术切除的晚期胰腺癌的一种较有效的姑息疗法[3]。由于植入的粒子具放射性,亦可对正常组织造成伤害,故植入点应尽可能接近病变区域。为了更好地进行粒子植入治疗,希望得到目标区域内较为精细的局部癌变组织的分布情况。而现有的分类方法,是提取一整块较大区域进行判别,区域的大小变化不灵活,同时也无法给出取样区内部的局部分布信息[4-5]。

本研究旨在对胰腺超声内镜图像以分块模式分类的方法,在图像中显示出较为精细的局部小块区域中癌症分布情况。为临床诊断及治疗粒子植入的位置等提供参考。

1 资料和方法

1.1 一般资料

实验数据为长海医院消化内科提供的胰腺EUS图像（超声仪型号:OLYMPUS EndoEcho UM2000,探头频率7.5 MHz）。包括153幅胰腺癌图像和63幅非胰腺癌图像共216幅作为训练及测试样本。所有胰腺癌病例均经EUS-FNA细胞学检查确诊。EUS图像上已由有经验的医生勾画出感兴趣的区域。

1.2 研究方法

使用自行开发的软件进行实验,先在感兴趣的区域中截取子图; 再根据预先给定的尺度（len）,以正方形对其分块（即正方形的边长为len）,并进行特征提取和模糊分类; 最终得到图像在分块后的尺度下的胰腺癌概率,并在图中显示各小块的分类结果。

1.2.1 已有的整块图像分类方法

先提取图像的纹理特征。

目前医院对于收入的控制措施更多地依赖于人工的审核，主要原因在于各系统、模块关联度不够，信息单向流动未形成闭环，数据未能相互印证，因此医院需对现行系统进行升级改造。由于医院系统众多，如果是一对一提供接口工程量大、成本高、可扩展性不强。医院需要建设数据集成云平台，由各类系统将各自数据提交给集成云平台，同时从平台上获取其他系统提交的数据，实现数据的双向流动，实现业务数据与收入数量相匹配。

图像的纹理包含了人类视觉系统用于解释和分析不同类型图像的重要信息,一般指图像基本元素在空间上的互相关联与排列[2]。图像的纹理特征种类繁多,已有的方法使用类间距等指标进行特征筛选,并综合考虑软件的实时性选择了以下22个特征进行整块图像的分类[4-6]:

首先,选取图像灰度均值特征。

其次,取20个灰度共生矩阵特征。他们都基于由Haralick等提出的图像二阶联合概率分布的矩阵。本研究构建0°、45°、90°、135°四个方向上的灰度共生矩阵,对每个矩阵提取能量、熵、惯性矩、相关、局部平稳5个特征。

最后,选取分形特征。近年来,分形维数特征被广泛应用于模式识别和纹理分析,本研究采用二阶多重分形维数特征,并使用差分数盒子法进行计算。

下面进行模糊分类。

对一个待识别的图像u,共有2个类别:癌症与非癌症。即对这个对象的判别有2种选择。在待识别图像中提取的纹理特征所构成的集合,对这2个类别都会有1个隶属度A,即对癌症和非癌症分别为A1(u),A2(u)。,图像u在某个类别下的隶属度数值越大,则其属于该类别的概率也越大[7]。

使用病例样本图像计算以上所述各个图像纹理特征的均值和方差,并加上一定的权系数,即可分别得到待识别图像u对癌症和非癌症的隶属度A1(u),A2(u)。最后输出一个归一化的评价结果:如结果越趋近于100%,说明是癌症的可能性越大; 越趋近于0%,说明不是癌症的可能性越大。

1.2.2 傅里叶功率谱方向性特征的引入

傅里叶功率谱方向性特征[8]的公式如下:

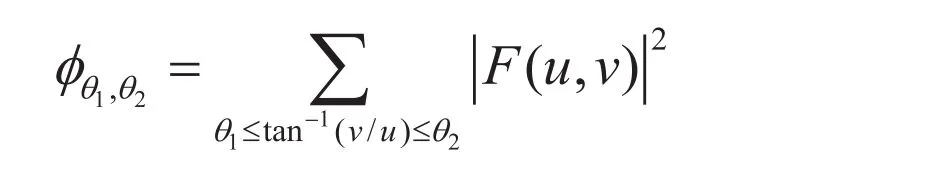
此特征在尺度较大时分类效果不明显,但在尺度较小时效果较好,如图1、2所示。

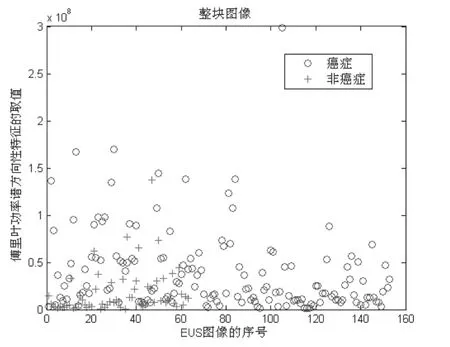
图1 整块较大尺度时傅里叶功率谱方向性特征的分类情况

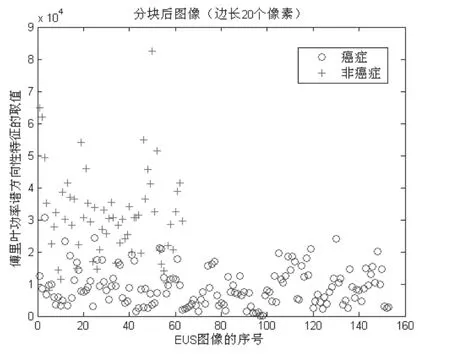
图2 分块尺度较小时傅里叶功率谱方向性特征的分类情况

值得注意的是,此种特征的绝对值随分块大小的变化而变化; 而实际进行分类时,尺度是任意变化的。故本研究将得到的特征值再除以该尺度下这个特征的均值,这样就使得其与分块的大小无关。其中,各个尺度下这一特征的均值采用如下方法得到:

先使用上述的样本分别计算癌症和非癌症类别在len为20、25、30、35、40、45和50（像素点）时这一特征的均值,再将得到的结果做多项式曲线拟合,如图3,4所示。

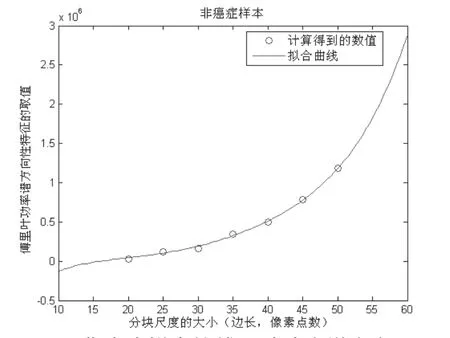
图3 非癌症样本的傅里叶功率谱方向性特征拟合曲线

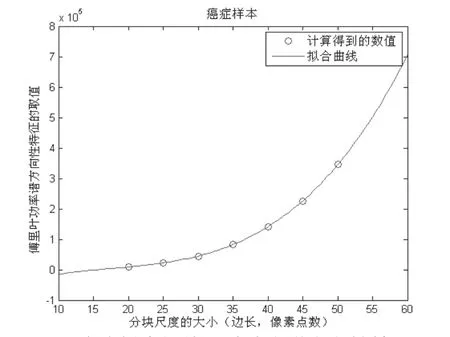
图4 癌症样本的傅里叶功率谱方向性特征拟合曲线

这样就近似地得到了特征的均值随分块大小变化的函数,分别为:

其中,αi、βi是多项式系数,Mean_c和Mean_nc分别为癌症或非癌症的特征均值。

1.2.3 实验过程

首先,在目标图像中选取一个方形的感兴趣区域,软件会先对整块区域进行胰腺癌或非胰腺癌的分类;接着会根据整块分类的结果计算傅里叶功率谱方向性特征; 最后根据指定的分块尺度重新对每一个小块进行分类,将分类的结果（为癌症的可能性）显示在小块的中央,并加上颜色调制便于观察（红色为可能性大于70%,黄色为可能性在40%～70%之间,绿色为可能性在40%以下）,同时亦可选择将本次分块分类的结果导出保存。分块的len可以步进的方式改变,步长可任意指定,len变化后软件能实时地更新结果并刷新显示。

由于分块len过小时大多数特征的分类效果都会变差,故在实验时需要将1个尺度下所有分块分类结果的均值与整块分类的结果进行比较。如结果差别较大,则说明len过小,得到的分类结果不正确。此时,应该增大len并重新分类。

2 结果

采用23组纹理特征,将所有分块分类结果的均值作为分类结果,如均值大于50%则判为癌症,小于50%则为非癌症。将上面提到的共216幅病例图像作为训练及测试样本,进行了10次随机实验,在分块尺度大于25（像素点）时,得到的分类正确率和原先整块分类[4]的正确率相同,为96.11%。

对癌症病例图像进行分块分类后,图5～8中红色较集中的区域即表示依照本研究的方法分类,癌症可能性较高的区域,可为医生的诊断以及粒子植入治疗的位置提供一个参考。

3 讨论

在实验中发现,上面提到的纹理特征随着分块len的变化而不同,其分类的效果也会有一定的改变。如灰度共生矩阵特征的分类效果会随着分块的变小而变差; 反之,傅里叶功率谱方向性特征的分类效果则会随着尺度的变小而变好; 均值特征,二阶多重分形特征对分块尺度的变化不敏感。

所以在实验中,对不同特征的权值,在分块尺度变化时也给予1个线性的修正。即随着分块尺度的变小,灰度共生矩阵特征的权值逐渐变小,傅里叶功率谱方向性特征的权值逐渐变大; 而均值特征,二阶多重分形特征的权值保持不变。

另外,由于癌症与非癌症的拟合函数有一定的差别,故此特征在计算时还需对目标图像是否为癌症先做1个初步的判断。所以在分类时先用前面的22个特征做1次整块图像的分类; 再根据得到的结果,计算给定分块尺度下的傅里叶功率谱方向性特征的值。

最后,针对是否使用本研究中的傅里叶功率谱方向性特征进行了对比实验（分块len为25个像素点）。发现对于癌症图像,使用了傅里叶功率谱方向性特征后分块分类的均值更趋向于100%,且图中红色及黄色的区域亦趋增多。而对于非癌症图像,使用傅里叶功率谱方向性特征后分块分类的均值更趋向近0%,且图中的黄色区域较少,绿色区域较多。可见使用这一特征的分类效果更好。给出了1组癌症图像和1组非癌症图像作为例子,如图5～ 8所示。

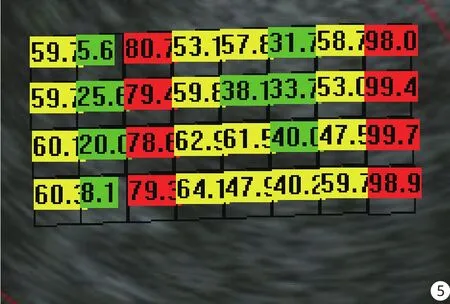
图5 癌症病例,未使用傅里叶功率谱方向性特征,各分块结果均值56.96%

图6 癌症病例,使用傅里叶功率谱方向性特征,各分块结果均值64.89%

图7 非癌症病例,未使用傅里叶功率谱方向性特征,各分块结果均值31.14%

图8 非癌症病例,使用傅里叶功率谱方向性特征,各分块结果均值25.57%

本研究采用了计算机图像处理及特征提取、模式分类的方法,对胰腺EUS图像进行了可变尺度的分块分类。得到了更为精细的局部癌症可能性较高的区域,可辅助医生进行诊断及指导治疗粒子植入。这样即能确保癌症高风险区受到足够的照射,又可将毗邻正常组织受到的照射伤害降至最小。

另外,本研究中对不同尺度下各特征的权值修正方法比较简单。寻求更为有效的修正方法则为今后研究的方向。

[1]杨杰,曲晓静,钟慧闽,等.超声内镜引导下细针穿刺对胰腺癌的诊断价值[J].实用医药杂志,2007,24(10):1178-1179.

[2]张敏敏,金震东,蔡哲元,等.计算机辅助判别超声内镜图像诊断胰腺癌的实验研究[J].中华消化内镜杂志,2009,26(4):180-183.

[3]Ducreux M,Boige V,Malka D.Treatment of advancedpancreatic cancer[J].Seminars in oncology,2007,34(11):25-30.

[4]蔡哲元,余建国,张敏敏,等.胰腺内镜超声图像纹理特征提取与分类研究[J].生物医学工程学进展,2008,29(3):141-145.

[5]ZhangMM,YangH,Jin ZD,et al.Digital imaging processing andclassificationbased on support vector machine of EUS images differentiate pancreatic cancer from normal tissue accurately:a pilot study[J].Gastrointestinal Endoscopy,2010,72(5):978-985.

[6]Xia Y,FengD,Zhao R.Morphology-Based Multifractal Estimat-ion for Texture Segmentation[J].IEEE Trans Image Process,2006,15(3):614-623.

[7]陈水利,李敬功,王向公,等.模糊集理论及其应用[M].北京:科学出版社,2005:170-175.

[8]Lendaris GO,Stanley GL.Diffraction pattern sampling for automaticpattern recognition[J].Proceedings of the IEEE,1970,58(4):198-216.