二维MPSTD算法的研究

张建萍

（华北电力大学 电气工程学院，河北 保定071003）

FPSTD算法于1997年最先被Q.H.Liu引入到电磁学中［1］，它的基本思想是：对 Maxwell方程中时间微商利用中心差分或高阶差分近似，对空间微分采用Fourier变换代替，并采用快速傅立叶变换（FFT）技术对离散傅立叶变换进行计算。与FDTD方法相比，FPSTD算法由于采用Fourier变换及反变换来实现Maxwell方程中场量空间导数的计算，理论上精度可以无限高，所以不存在由于空间网格划分带来的误差。在满足Nyquist采样定理的情况下，在每一个最小波长上只需要设置2个采样点，即可实现对电磁问题的准确分析。目前，该算法已经被成功地应用于求解空间简单目标的散射特性、建筑物内电波场强分布和模拟探地雷达分析地下简单目标体的散射特性等。然而，由于FFT具有固有的周期性，FPSTD算法只适用于分析周期问题，如均匀介质空间或者变化不大的非均匀介质空间。若将其用于复杂媒质电磁问题的分析时，如金属物体和拥有不连续媒质分布的问题时，由于Gibbs现象的影响，它的计算精度是较低的；其次，若将该算法用于复杂几何形状目标问题的分析时，目标外形的阶梯近似使得该算法不能对目标外形进行准确描述，造成了计算精度的下降。上述两点使得该方法的应用受到极大的约束。MPSTD算法于1996年被A.V.Kabakian引入到计算电磁学［2］。它的基本思想是：将整个计算域剖分成若干个与所分析电磁问题共形的曲边四边形子域（二维电磁问题）或曲面六面体子域（三维电磁问题），切比雪夫选配方法被单独用在每个子域里进行计算，子域之间通过子域分界面上的匹配边界条件来实现信息的传递。已有的文献表明：MPSTD算法每最小波长只需要设置π个采样点即可实现对电磁问题的准确分析。由于共形子域划分的应用和多域策略的引入，MPSTD算法比FPSTD算法具有更大的灵活性和适用性［3，4］。

由于PSTD算法采用傅立叶选配方法或切比雪夫选配方法来求解Maxwell方程中场量的空间导数，所以均具有谱域计算精度。同时，由于PSTD方法每最小波长只需要设置2个或π个采样点，因而它对计算机的内存需求大大降低，计算量也同时大大减少，已有大量文献表明PSTD算法在许多应用方面都显得比FDTD更加有效。该算法作为一种新颖的电磁场数值方法，在计算电磁学中已经得到越来越多的重视。

从以上的简要描述中可以看出多区域伪谱时域算法是一种高阶的、灵活的、有效的数值算法，具有很强的实用性。本文就二维多区域伪谱时域算法展开理论的研究［5－9］。

1 曲线坐标下的Maxwell方程

由Maxwell方程

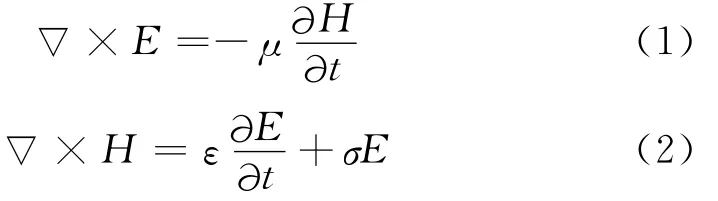
考虑一个各向同性，导电的不均匀媒质，具有介电常数ε、磁导率μ和电导率σ。对于二维TMz极化的Maxwell方程可表达为

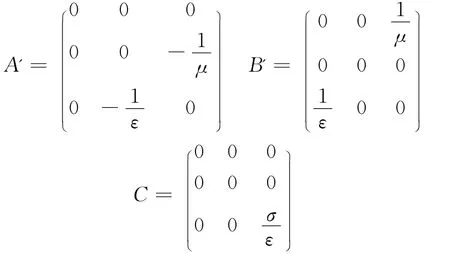
矩阵形式为：

式中，q＝（Hx，Hy，Ez）T。

采用坐标变换将坐标系（x，y）中具有曲边界的子区域映射成坐标系（ξ，η）中的单位正方形。引入坐标变换关系为：ξ＝ξ（x，y），η＝η（x，y），式（6）变为：

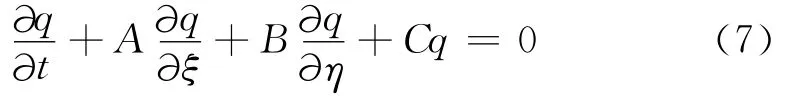
式中，q＝（Hx，Hy，Ez）T

且ξx＝∂ξ／∂x，ξy＝∂ξ／∂y，ηx＝∂η／∂x，ηy＝∂η／∂y。

2 切比雪夫选配方法

由于切比雪夫选配方法具有十分优越的近似特性，因此该方法被广泛地应用于偏微分方程的求解中。K阶切比雪夫多项式定义为：

TN（x）＝cos（Ncos－1（x）） 其中｜x｜≤1

在坐标系（ξ，η）中，定义单位正方形上的Chebyshev－Gauss－Lobatto配置点为：

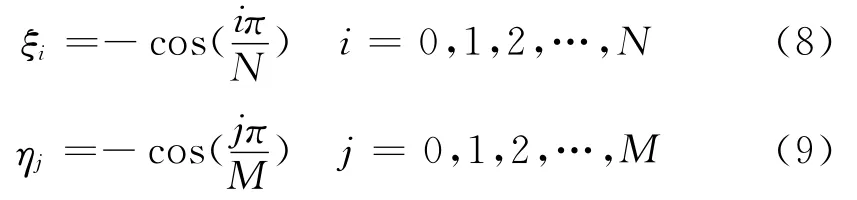
采用张量积Chebyshev－Lagrange多项式，q（ξ，η）为

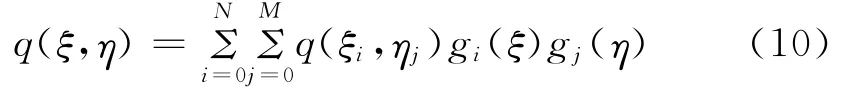
式中，gi（α）为Lagrange差值多项式

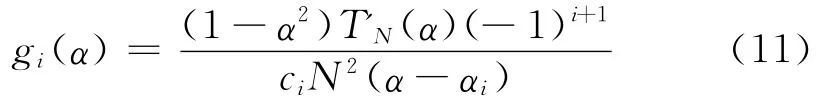
式中，α＝（ξ，η）。

于是场量q（ξ，η）定义在网格点上的空间偏导数为：

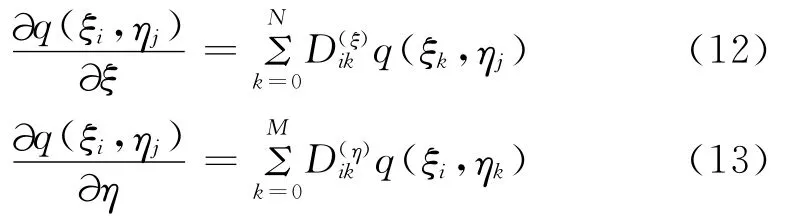
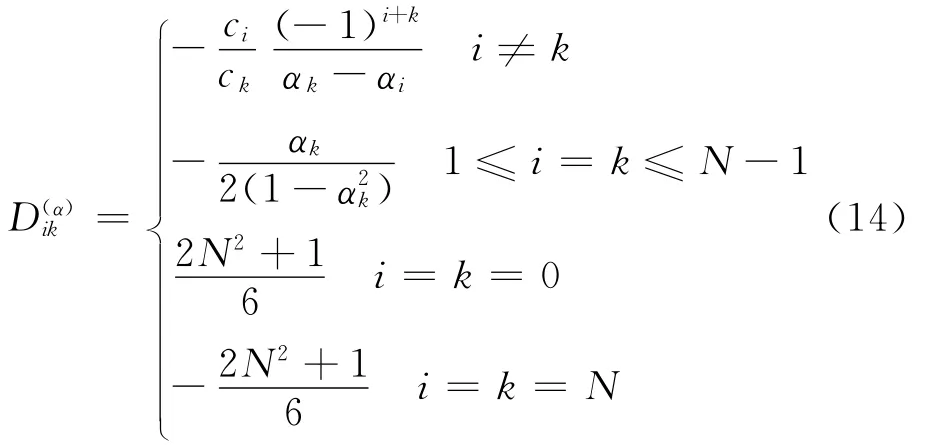
3 特征变量子域匹配条件

为了获得整个区域的解，就需要采用匹配条件将每个子区域中的解联系起来。特征变量法是一种有效地施加边界条件的方式。将式（7）中的矩阵A对角化可得

其中

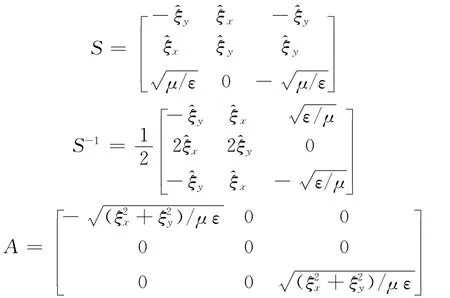
则特征矢量可得

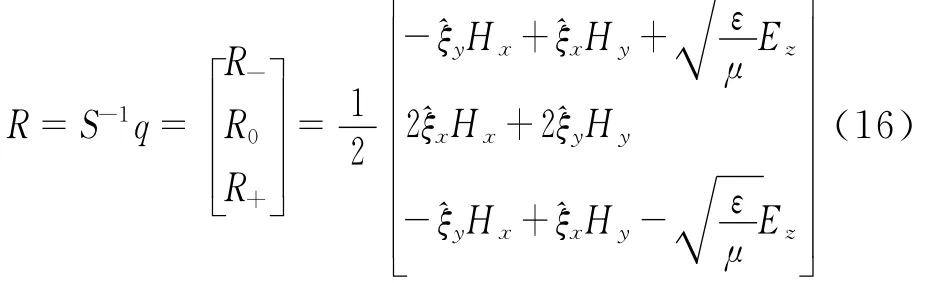
式中，特征变量R－代表沿－ξ传播的特征波的幅度；特征变量R＋代表沿＋ξ传播的特征波的幅度；特征变量R0代表不传播的特征波的幅度。对角矩阵Λ中对角线上的元素对应着特征波传播的速度。矩阵B的特征变量类似于矩阵A的特征变量。

一般情况下在两个子区域之间有两类交界面：一类是两个子区域具有不同的媒质；另一类是两个子区域具有相同的媒质。对这两类情况的处理方法是不同的。首先考虑两个相邻的子区域具有相同媒质的情况。假定ξ轴是从子区域1指向子区域2。在这种境况下，在交界面上匹配特征变量可得

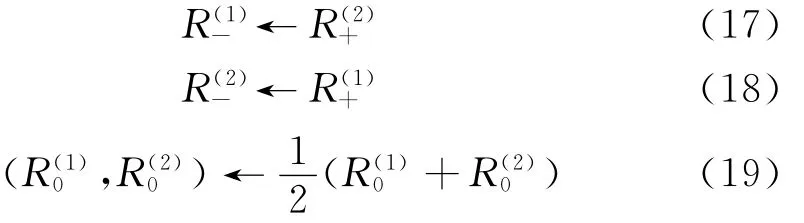
式中，上标（1）和（2）分别定义为子区域1和子区域2。式（17）～式（19）分别代表的含义如下：

（1）入射的特征变量波是由相邻子区域的出射的特征变量波所决定；

（2）不传播的特征变量波保持连续；

（3）出射的特征变量波不改变地进入下一子区域。

对于两个相邻的子区域具有不同媒质的情况，在交界面上施加物理边界条件。对于介质交界面，保持切向电磁场连续：

式中，下标t表示交界面处的切向场分量。

对于理想导体，切向电场和法向磁场为零：

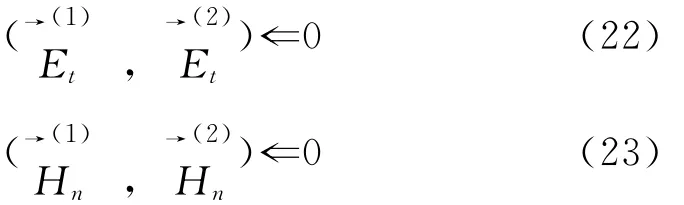
式中，下标n表示交界面处的法向场分量。

4 完全匹配层

在时域方法中一个关键的问题就是采用吸收边界条件去截断无限大的计算区域，使得整个计算在有限区域中进行且在吸收边界处不引入反射。这里采用一种系统的方法去推导良态提出的（well－posed）有耗媒质理想匹配层（PML）公式。

根据复坐标构架技术引入复坐标构架变量

式中，aη（η＝x，y）是一个标量系数；wη（η＝x，y）是衰减系数。为了简单起见，令ax＝ay＝1。

下面推导有耗媒质PML公式：

将式（3）～（5）变成频域形式

经过适当运算，变成时域形式得：

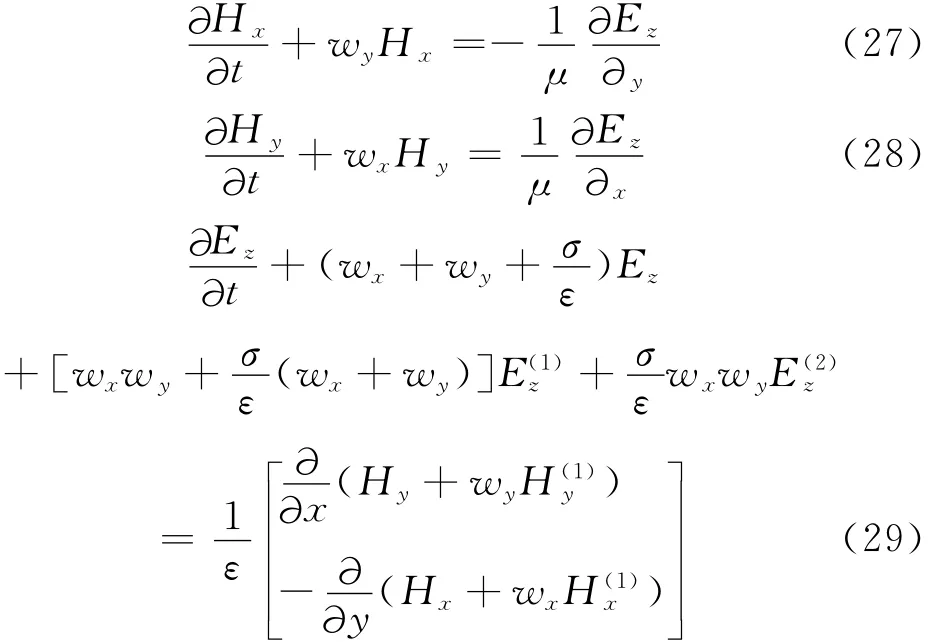
则式（27）～（29）变为：

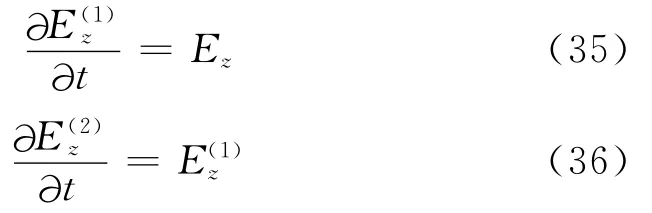
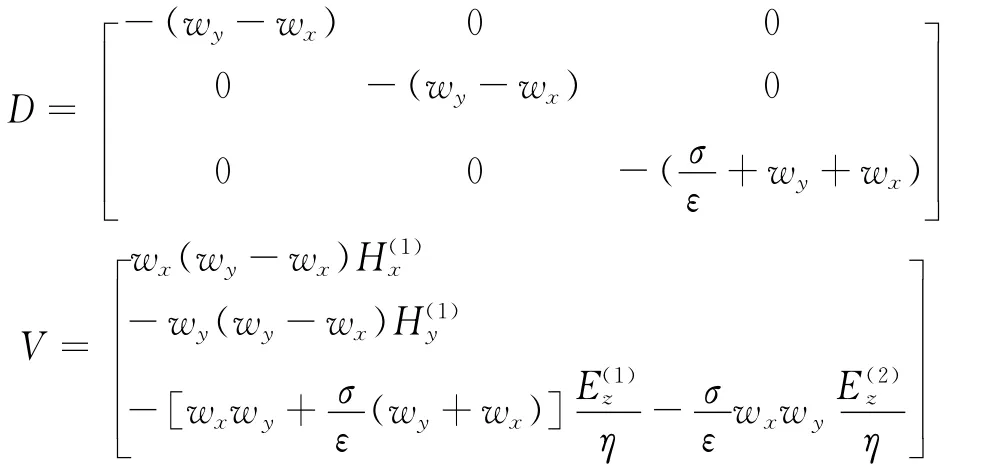
注意到上面的PML方程是不分裂场形式的。除了一些低阶项以外，它和原始的Maxwell方程一样都是对称的双曲系统，因此这个PML是 Well－posed。当σ＝0时，有耗媒质的ABC就变为无耗的ABC；当wx＝wy＝0时，PML方程就退化为最初的 Maxwell方程。

5 时间积分方法

采用五步、四阶、低存储的Runge－Kutta方法进行时间积分。将式（7）表示为

定义qn＝q（tn），tn＝nΔt，其中Δt是时间步间隔，则对于2 N存储，M步K 阶Runge－Kutta方法可表示为

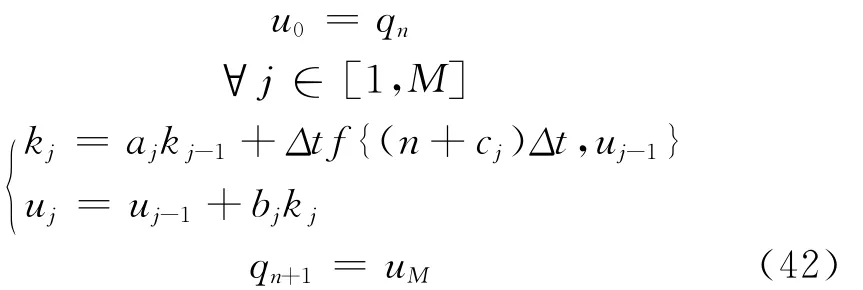
6 结 论

本文分析了便于复杂媒质求解的MPSTD技术，探讨了MPSTD所使用的切比雪夫选配方法，子域匹配，完全匹配层（PML）。MPSTD算法的实现归结为以下五个步骤：（1）计算模型的建立。首先，根据待分析问题的特征，选择合理的坐标系（本论文选择直角坐标系），建立准确的计算模；其次，根据计算模型的特征，进行合理的子域剖分，并根据每个子域的特点，选择每个子域剖分的网格数目；最后，选择合理的子域到单位正方形之间的坐换关系式；（2）时间步推进。选择合理的时间步方法处理Maxwell微分方程组中关于时间的偏微分计算（本论文选择Runge－Kutta法）；（3）空间导数的计算。在各子域内部采用切比雪夫谱选配方法计算Maxwell微分方程组中的空间导数，并采用匹配边界条件处理子域间分界面上的场（本论文选择基于特征变量CV的子域分界面匹配条件）；（4）吸收边界处理。MPSTD算法和其它数值计算方法一样，在计算“开放”电磁系统时，必须人为设定一个吸收边界进行截断（本论文选择的是PML吸收边界条件）；（5）计算结果的提取和输出。根据仿真目的的不同，选择相应的参数提取方式，实现算法的后处理。

［1］Liu Q H.The PSTD Algorithm：a Time－domain Method Requiring Only Two Cells Per Wavelength［J］.Microwave Opt Technol Lett，1997，15（3）：158－165.

［2］Kabakian A V.A three－dimensional spectral collocation time－domain solver for electromagnetic wave scattering［C］.New York：Aircraft Industries Association of America，1997.

［3］杨 虎.多区域时域伪谱算法在电磁分析中的理论和应用研究［D］.长沙：国防科学技术大学，2006.

［4］史 琰.高阶时域电磁计算方法［D］.西安：西安电子科技大学，2005.

［5］姜永金，柴舜连，毛钧杰.MPSTD算法子域分界面匹配条件的比较研究［J］.电波科学学报，2010，（1）：18－20.

［6］Yang B，Hesthaven J S.Multidomain pseudospectral computation of Maxwell＇s equations in 3Dgeneral curvilinear coordinates［J］.Appl.Numerical Math，2000，33：281－289.

［7］Fan G X，Liu Q H，Hesthaven J S.Multidomain pesudospectral time－domain simulations of scattering by objects buried in lossy media［J］.IEEE Transactions on Geoscience and Remote Sensing，2002，40（6）：1366－1373.

［8］Fan G X，Liu Q H.A Well－Posed PML Absorbing Boundary Condition for Lossy Media［C］.IEEE Antennas and Propagation Society International Symposium，2001.

［9］Fan G X，Liu Q H.A Strongly Well－Posed PML in Lossy Media［C］.IEEE Antennas and wireless propagation letters，2003，（2）：97－100.