三相光伏并网发电系统MPPT的研究
金志辉
(上海理工大学 光电信息与计算机工程学院,上海200093)
1 光伏并网系统概述
随着全球能源危机和环境污染日趋严重,有效、合理利用现有资源,保护环境,加快可再生绿色能源利用的研究已成为世界关注的焦点。在可再生能源中,太阳能是利用最灵活、最可行的一种能源,它具有无污染、无噪声、取之不尽、用之不竭等优点。光伏发电是太阳能最有价值的利用途径之一,具有广阔的发展前景,越来越受到关注,在未来的供电系统中将占有重要的地位。光伏并网系统原理图如图1所示。

图1 光伏并网系统图
光伏电池是一种复杂的非线性直流电源,它的输出特性受光照强度、温度、湿度、压强、风速等多方面的外界因素影响,其中光强和温度的影响最大。即使在外部环境稳定的情况下,光伏阵列的输出功率也会随着外部负载的变化而变化,只有当外部负载与光伏阵列达到阻抗匹配时,光伏阵列才会输出最大功率,此时称光伏阵列工作在最大功率点(Maximum Power Point MPPT)[1]。为了有效提高光伏电池的工作效率,需对光伏电池的输出进行最大功率跟踪,使其工作在最大工作点。最大功率控制方法也有一个发展过程,早期的光伏系统采用恒定电压控制方法,这种方法的优点是简单易行,而且基本可以跟踪最大功率点。但随着电力电子及控制技术的发展,这种方法的简单性与其造成的能量损失相比已显得很不经济。因此一些新的控制方法应运而生,如功率反馈法、扰动观测法、导纳增量法、模糊控制法等,本文采用的是基于最优梯度法的MPPT控制法。
2 光伏电池的特性
光伏电池是利用半导体材料的光伏效应而制造的。所谓的光伏效应是指半导体材料吸收光能,由光子激发出的电子-空穴对经过分离而产生电动势的现象。光伏电池组件的I-U 特性随光照强度S(W/m2)和温度t(℃)而变化,即I=f(U,S,t)。其I-U 函数[2]如下:
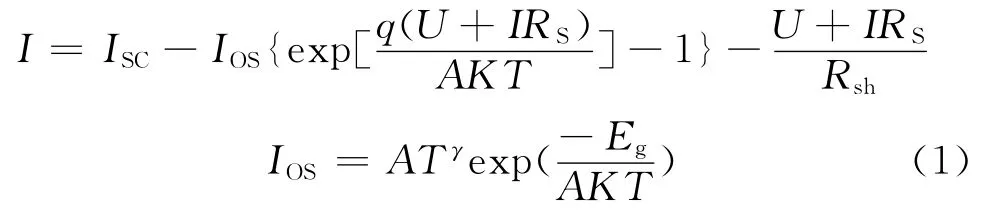
理想情况下,RS可近似为零,Rsh近似为无穷大,式(1)可简化为:
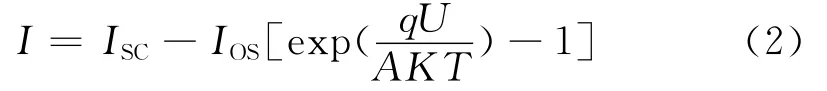
式中,I,ISC、IOS为光伏电池的输出电流、短路电流、通过P-N结扩散电流;RS为串联电阻;Rsh为旁漏电阻;q为电子电荷;K为波尔兹曼常数;T为绝对温度;A为光伏电池中半导体电池的p-n结系数。
3 Buck-Boost电路状态空间建模
本文采用Buck-Boost转换电路对光伏发电系统进行最大功率跟踪,即在光伏阵列和DC/AC之间加一个DC/DC变换电路,通过改变DC/DC变换器中功率器件的导通率ΔD来调整、控制光伏阵列,使其工作在最大工作点,从而实现最大功率的跟踪,如图2所示。要用斩波器实现最大功率跟踪控制,首先要建立斩波器的数学模型[3,4]。
Buck-Boost电路附有EMI滤波器并含有配电感抗,在状态空间建模时将其忽略不计。此外,IGBT认为是理想开关。IGBT在PWM波的每个周期中存在ON和OFF两种开关状态。

图2 Buck-Boost转换电路
TGBT在ON状态下,有如下关系式:
TGBT在OFF状态下,有如下关系式:
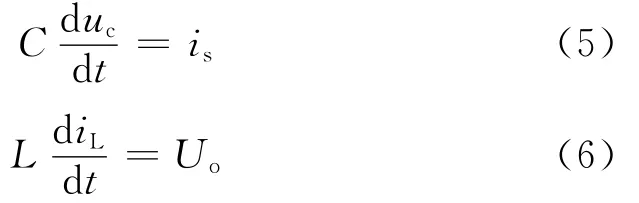
DC/DC的导通率设为D,关断率为D′,上述式子经整理可得出Buck-Boost电路状态方程:
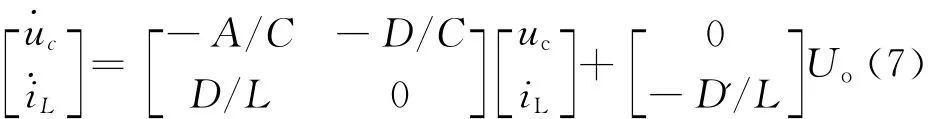
由上述式子,可得出传递函数:
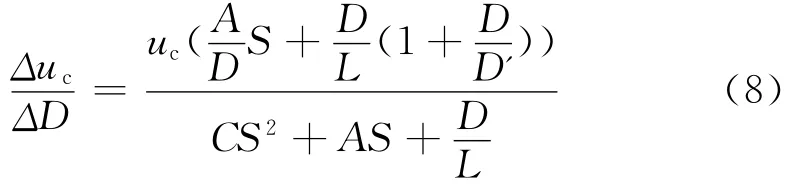
4 MPPT的控制
光伏阵列的开路电压和短路电流在很大程度上受日照强度和温度的影响,其功率输出随日照强度的增强而增大,而温度上升将使光伏阵列的开路电压下降,短路电流则轻微增大。因此,总体效果会造成光伏阵列的输出功率下降。为此,光伏阵列必须实现最大功率点跟踪控制,以便阵列在任何日照强度和温度下都能获得最大功率输出。
MPPT的实质[5]是一个自寻优过程,即通过控制端电压,使光伏阵列能在各种不同的日照和温度环境下智能化的输出最大功率。现有最大功率点跟踪控制方法有定电压、功率回授、电导增量、短路电流检测、扰动观测法等。本文光伏系统中MPPT控制是通过控制Buck-Boost电路占空比来实现,控制方法采用基于最优梯度法的MPPT控制方法。

图3 P-U特性曲线
4.1 最优梯度法原理
最优梯度法[6,7]是一种以梯度法(Gradient method)为基础的多维无约束最优化问题的数值计算法。它的基本思想是选取目标函数的负梯度方向作为每步迭代的搜索方向,逐步逼近函数的最小值。梯度法是一种传统且被广泛运用于求取函数极值的方法,该方法运算简单。
最优梯度法的定义如下:若一欧式空间n维函数f(f∈En),为连续且可微分一次,故2f(x)存在且为一n维的列向量(row vector),我们定义一n维的行向量(column vector)g(x)=2f(x)t,为了方便定义gk为:
定义梯度法之迭代演算法如下:

式中,ai为一非负值的常数,搜寻函数的最小点是沿着正梯度gi的方向搜寻。
4.2 基于最优梯度法的MPPT控制
光伏电池的P-U特性曲线有强烈非线性,而最大功率跟踪法的目的是要在P-U特性曲线上求得曲线的最大值。据最优梯度法的原理可知,使用最优梯度法可以实现 MPPT。对于光伏系统,应选正梯度方向,逐步逼近函数的最大值,得到令人满意的结果。
由光伏电池的电气特性可知,若忽略串联电阻的效应,可得如下电压和功率之间的关系:
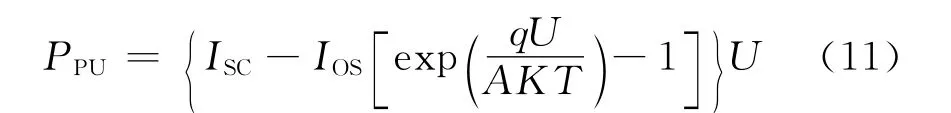
式(11)中,函数PPU为一非线性函数,且连续一次可微,又函数PPU以电压U作为唯一的变量,则gi为:
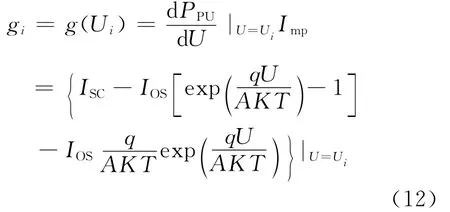
由式(10)可知,迭代算法可写成式(13):

由功率电压特性曲线图4可知,由于端电压有界,故利用梯度法对光伏阵列进行最大功率跟踪,所搜寻到的最大功率点是全域的。

图4 最优梯度法进行MPPT的搜索过程
利用梯度法进行MPPT,保留了扰动观察法的优点,一个类似动态的扰动量可以改变太阳能输出功率曲线上电压的收敛速度。如图4所示,当工作点位于最大功率点左侧时,电压以较大的幅度增加;当工作点位于最大功率点附近时,此时斜率较小,则提供较小的扰动量。反之,当工作点位于最大功率点右侧时,电压以较大的幅度减少。因此,便可改善在最大功率输出点附近振荡的情况,保证跟踪过程的稳定性和快速性。
5 仿真结果与分析
根据上述研究,按照图5的原理,基于 MATLAB/Simulink建立通用光伏阵列仿真模型[8]。图6为光伏阵列模块外观,其中T、S、Tref、Sref分别为实时环境温度、太阳辐射强度、环境温度参考值和太阳辐射强度;U+、U-分别为光伏阵列输出端的正极和负极。其中,Tref=25°C,Sref=1 000W/cm2。图7为光伏阵列最大功率跟踪MPPT的MATLAB仿真图,该输入电源为本文所建立的光伏阵列模块,DC/DC最大功率跟踪模块由MOSFET管、二极管和电感组成的Boost-Buck电路。

图5 MPPT控制结构原理图
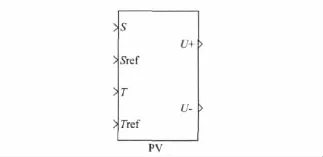
图6 光伏阵列的MATLAB封装模块
利用最优梯度法进行MPPT,即选取PPU函数的正梯度方向作为每步迭代的搜索方向,以光伏阵列电压U作为唯一变量,改变电压扰动量,逐步逼近光伏阵列输出的最大功率。实际工作中,光伏阵列不会达到额定的峰值功率,因此仿真中设定光伏阵列的最大输出功率6W,开路电压280V。
仿真结果,当日照强度从800W/cm2变化到1 000W/cm2时,图8是在日照强烈变化时MPPT控制光伏阵列输出电流仿真波形;图9为日照强烈变化时MPPT控制的光伏阵列输出电压;图10日照强烈变化时MPPT控制的光伏阵列输出功率。从图中可以看出,出现扰动后,经过0.02s,光伏阵列输出电流能很快进行调整并趋于稳定。可以得出,该方法响应速度快,可基本消除光伏阵列输出功率在最大功率点附近的功率振荡。
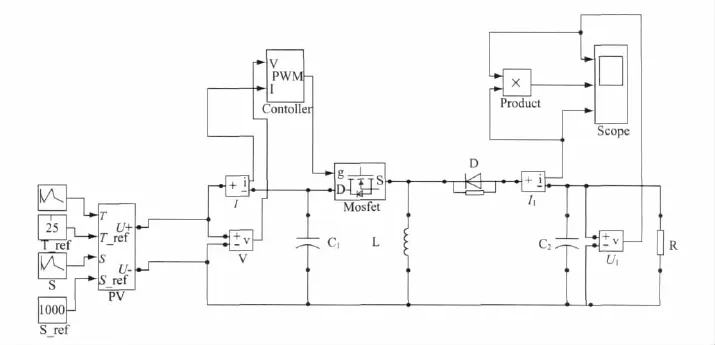
图7 光伏阵列最大功率跟踪MPPT的MATLAB仿真图

图8 日照强烈变化时MPPT控制光伏阵列输出电流波形
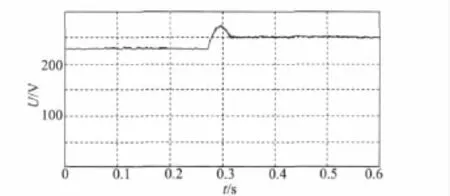
图9 日照强烈变化时MPPT控制的光伏阵列输出电压
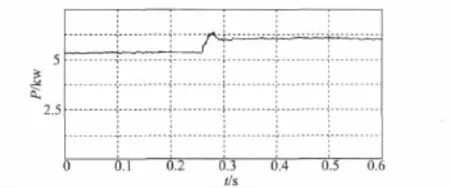
图10 日照强烈变化时MPPT控制的光伏阵列输出功率
6 结 论
仿真结果表明了在该MPPT控制方法作用下,光伏阵列的输出电流和输出电压均没有振荡,只存在一定的波动,因此该方法可基本消除光伏阵列输出功率在最大功率点附近的功率振荡。同时该方法在日照突变情况下,能使光伏阵列迅速重新工作在最大功率点。同时并网侧电压、电流基本与电网侧的电压同相。
因此,基于该MPPT控制方法的光伏系统在日照稳定和日照突变情况下均能较好地实现MPPT控制,基本消除了最大功率点处的功率振荡现象,且对日照的变化有良好的快速跟踪能力。
[1]HohmD P,RoPPM E.Com Parative study of maximum power point traeking algorithms using an experimental,programmable,maximum power point tracking test bed[C].Photovoltaic Specialists Conferenee,2000.Conference Record of the Twenty-Eighth IEEE,2000:1699-1702.
[2]Sang-Soo Park,An Optimized Sensorless MPPT Method For PV Generation System[J].IEEE Tran Power Delivery,2009,5,722-724.
[3]Kasa N,lida T.Maximum power point tracking with capacitor identifier for photovoltaic power system[J].IEE Proc-Electr,2000,147(6):497-502.
[4]冯垛生.太阳能发电原理与应用[M].北京:人民邮电出版社,2008.
[5]Xuanyuan Wang,Kazerani M.A novel maximum power point tracking method for photovoltaic grid-connected inverters[C].Industrial Electronics Society,The 29th Annual Conference of the IEEE,2003,3:2332-2337.
[6]闵江威.光伏发电系统的最大功率点跟踪控制技术研究[D].武汉:华中科技大学,2006.
[7]Samimi J,Soleimani E A,Zabihi M S.Optimal Sizing of Photovoltaic Systems in Varied Climates[J].Solar Energy.1997,60(2):197-107.
[8]茆美琴,余世杰,苏建徽.带有 MPPT功能的光伏阵列Matlab通用仿真模型[J].系统仿真学报,2005,17(5):1248-1251.

