关于核为对称-1齐次的Hilbert型不等式的加强

贺乐平



关于核为对称-1齐次的Hilbert型不等式的加强

贺乐平

(吉首大学 数学与计算机科学学院, 湖南 吉首, 416000)

Hilbert序列算子; Hilbert不等式;函数; 权函数; Hölder不等式

本文的目的是利用改进的Hölder不等式对式(2)进行加强, 从而建立一些新的不等式.

1 引理及其证明

为方便起见, 先介绍一些定义和符号:

证明参见文献[4].

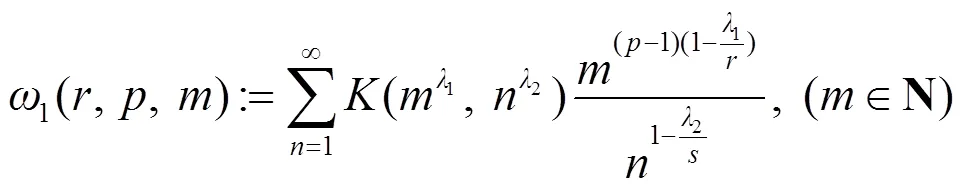
则有:

证明过程参见文献[3].

2 主要结果

为了方便起见, 再引入一些符号:

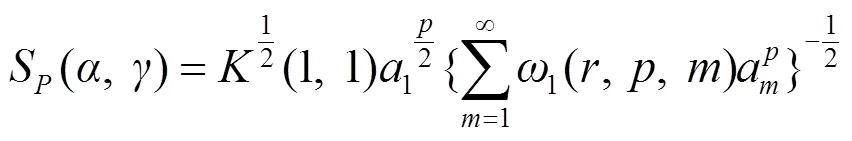
证明 由引理1及引理2有:

故式(9)成立.

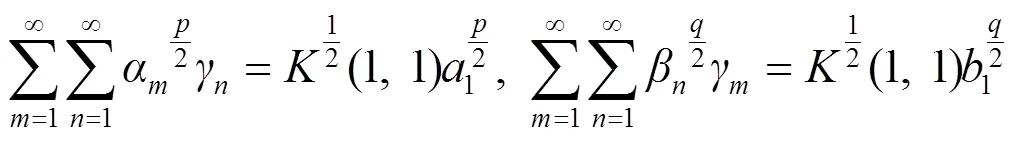
由引理1, 有:

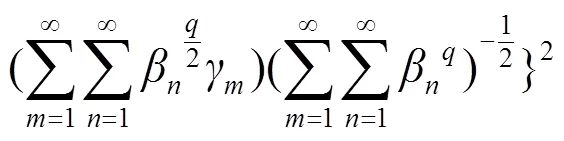
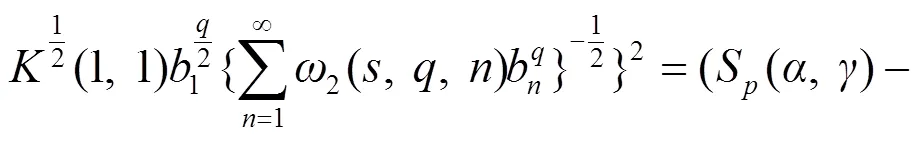
证毕.

注 式(9)是文献[3]中定理1.3的改进式.

[1] Yang Bicheng. On Hardy-Hildert's integral inequlity[J]. J Math Anal Appl, 2001, 261: 296-306.

[2] 杨必成. 关于一个推广的Hardy-Hilbert不等式[J]. 数学年刊, 2002, 23A(2): 247-254.

[3] 金建军. 关于核为对称-1齐次的Hilbert型不等式[J]. 数学学报, 2009, 52A(4): 799-806.

[4] He Leping, Gao Mingzhe, Jia weijian. On a New Streng-thened Hardy-Hilbert’s Inequality[J]. Journal of Mathe-matical Research and Exposition, 2006, 26(2): 276-282.

On the strengthen of Hildert type inequality with symmetric homogeneous kernel of-1-order

HE Le-ping

(College of Mathematics and Computer Science, Jishou University, Jishou 416000, China)

A Hildert type series operator and its norm were studied. A improvement of Hildert type inequality with symmetric homogeneous kernel of-1 -order, some new inequalities are established.

Hilbert series operator; Hilbert inequality;function; weight function; Hölder inequality．

10.3969/j.issn.1672-6146.2011.03.003

O 178

1672-6146(2011)03-0006-02

2011-04-27

国家自然科学基金资助项目(10871081)

贺乐平(1965-), 男, 教授, 主要研究方向为特殊函数论及其应用. E-mail: jdlepinghe@163.com

(责任编校: 刘晓霞)